(강의정리) 확률 및 통계

이 포스트는 한양대학교 이상화 교수님의 「확률 및 통계」 강의에 대한 요약입니다. 이 강의는 총 21강으로 되어 있고 확률과 통계에 관한 전반적인 사항을 다루는 것 같습니다.

강의 내용을 아주 자세하게는 적지 않고 간략하게만 적어나갈 예정입니다. 깔끔하게 적으려다보면 시간이 많이 걸리거나, 아예 안하게 되는 경우도 있어서, 조금 간단하게 적게 될 것 같습니다. 그래도 쓰고 고치고 하다보면 잘 정리될 수도 있을 것 같습니다.

기본적으로는 강의의 내용을 따라가지만, 강의의 내용만으로는 다 채워지지 않는 부분들이 있습니다. 예를 들어, 강의에서는 증명이 생략되는 경우도 많고, 개념의 의미가 완벽하게 설명되지 않는 경우도 있습니다. 이런 미흡한 부분은 다른 여러 자료들에서 채워넣으려고 했습니다.

강의의 회차를 나타낼 때에는 꺽쇠괄호를 사용했습니다. 예를 들어 $\langle02\rangle$라고 쓰면 이것은 2회차 강의 내용 또는 2회차 강의의 정리를 뜻합니다. 중요한 식을 나타낼 때에는 $(\ast)$, $(\ast\ast)$, $(\ast\ast\ast)$와 같은 기호를 사용했습니다. 이 식번호는 회차마다 초기화됩니다.

21강의 내용을 모두 한 포스트에 넣으려다보니 내용이 상당히 방대합니다. 그래서, 페이지의 모든 수식이 완전히 조판되는 데에는 약간의 시간(1분)이 걸립니다.

일단 17강까지의 내용에 대해서는 다 정리해보았습니다. 18강부터의 내용은 일단 보류합니다. 이정도에서 매듭을 짓고, 나중에 시간이 나면 뒷부분도 채우든지 하겠습니다.

01 조건부확률과 Bayes 정리

(1) sample space

확률에 대해 공부할 때 가장 먼저 배우는 것은 당연히 표본공간(sample space)입니다. 고등학교 이후의 과정에서 확률은 항상 집합의 관점에서 이해됩니다. 표본공간 또한 집합으로, 보통 $S$로 적습니다. 표본공간이란 어떤 시행(trial)에 대하여

나타날 수 있는 가능한 모든 결과(outcome)들의 집합

을 말합니다. 이러한 결과들은 근원사건(elementary event)이라고도 불립니다.

예를 들어, 주사위를 하나 던지는 시행을 한다면

\[S=\{1,2,3,4,5,6\}\]

이고, 동전을 하나 던지는 시행을 한다면

\[S=\{H,T\}\]

입니다.

(2) event, probability

확률은 보통 $P(A)$로 표시하는데, 여기에서 $A$는 사건(event)이라고 부릅니다. 이때, 사건은 $S$의 부분집합입니다. ($A\subset S$)

\[P(A)=\text{the probability that the outcome belongs to $A$}\]

예를 들어, 주사위를 한 번 던지는 시행에서 짝수 눈이 나올 사건을 $A$라고 하면

\[A=\{2,4,6\}\]

이고, $5$가 나오는 사건을 $B$라고 하면

\[B=\{5\}\]

입니다. 이때, $A\subset S$, $B\subset S$인 것입니다.

강의에서 ‘사건’에 대한 설명은 여기까지입니다. 더 나아가, 사건을 엄밀하게 정의하려먼 $\sigma$-algebra라는 개념을 도입해야 합니다. 사건은 $S$의 부분집합이라고 했지만, 모든 $S$의 부분집합이 사건은 아닐 수도 있습니다.

$\Sigma$가 $S$의 부분집합들의 집합이면서 다음의 세 성질들을 만족시키면 $\Sigma$를 $\sigma$-algebra라고 부릅니다. 그리고 $\Sigma$의 원소를 사건으로 정의합니다.

• $\Sigma$는 $S$를 원소로 가집니다 ; $S\in\Sigma$
• $\Sigma$는 차집합에 대해 닫혀있습니다 ; $A,B\in\Sigma$이면 $A-B\in\Sigma$입니다.
• $\Sigma$는 countable union에 대해 닫혀있습니다 ; $A_1,A_2,\cdots\in\Sigma$이면, $\bigcup_iA_i\in\Sigma$입니다.

따라서 $\varnothing$과 $S$는 항상 사건입니다. 이때, $\varnothing$을 공사건, $S$를 전사건이라고 부릅니다.

배반사건

두 사건 $A$와 $B$가

\[A\cap B=\varnothing\]

이면, $A$와 $B$가 서로 배반사건(exclusive events)이라고 말합니다. 이것은 두 집합이 서로소(disjoint)인 것과 대응되는 개념입니다.

세 개 이상의 사건들에 대해서는 배반이라는 말이 두 가지의 의미를 가지게 됩니다. $A$, $B$, $C$가 사건일 때,

\[A\cap B\cap C=\varnothing\]

이면, 세 사건이 mutually exclusive하다고 말합니다. 만약

\[A\cap B=\varnothing \quad\&\quad B\cap C=\varnothing \quad\&\quad C\cap A=\varnothing\]

이면, 세 사건이 pairwisely exclusive하다고 말합니다. 일반적으로, 사건 $A_1$, $A_2$, $\cdots$, $A_n$에 대하여

\[A_1\cap A_2\cap\cdots\cap A_n=\varnothing\]

이면, $A_i$들이 mutually exculsive하다고 말하고,

\[i\neq j\quad\Rightarrow\quad A_i\cap A_j=\varnothing\]

이면, $A_i$들이 pairwisely exclusive하다고 말합니다.

확률

한편, $P$는 확률측도(probability measure)라고 불립니다. 확률측도란 전사건에 대한 측도가 1인 measure(측도)를 말합니다. 다시 말해, 다음 세 성질을 만족시키는 $P$를 probability measure라고 부릅니다.

• $P$는 $P:\Sigma\to[0,1]$인 함수입니다.
• $P$는 countably additive합니다 ; $A_i\in\Sigma$가 서로 배반사건일 때 $P\left(\sum_{i=1}^\infty A_i\right)=\sum_{i=1}^\infty P(A_i)$
• $P(\varnothing)=0$, $P(S)=1$ 입니다.

예를 들어, 주사위를 하나 던지는 시행에서 $\Sigma$를 $S$의 멱집합(power set, $S$의 모든 부분집합들의 집합)이라고 하고 $P$를

\[P(A) =\frac{n(A)}{n(S)}\]

로 정의하면, $\Sigma$는 $\sigma$-algebra이고 $P$는 probability measure입니다. (단, 유한집합 $X$에 대하여 $n(X)$는 그 집합의 원소의 개수입니다.)

이렇게 정의한 $P$는 보통 주사위 문제를 풀 때 사용해왔던 그 $P$와 의미가 일치합니다. 아까 $A=\{2,4,6\}$, $B=\{5\}$로 두었었는데, $A\in\Sigma$, $B\in\Sigma$이고

\[\begin{align*} P(A)&=\frac{n(A)}{n(S)}=\frac36=\frac12\\ P(B)&=\frac{n(B)}{n(S)}=\frac16 \end{align*}\]

이기 때문입니다.

(3) coditional probability

두 사건 $A$, $B$에 대하여 사건 $A$가 발생했을 때 사건 $B$도 발생할 확률을 $P(B|A)$라고 쓰고,

\[P(B|A)=\frac{P(B\cap A)}{P(A)}\]

로 정의합니다.

이것은 마치, $A$를 sample space로 보는 것과 같습니다. 마찬가지로, 일반적인 확률 $P(A)$도 $P(A|S)$와 같이 해석할 수 있습니다.

(4) law of total probability

사건 $A_1$, $\cdots$, $A_n$에 대하여, $A_i$들이 pairwisely exclusive하고 $A_i$들의 합집합이 $S$이면, 다시 말해

\[i\neq j\quad\Rightarrow\quad A_i\cap A_j=\varnothing\]

이고,

\[A_1\cup A_2\cup\cdots\cup A_n=S\]

이면, $A_1$, $\cdots$, $A_n$가 $S$의 partition(분할)이라고 말합니다.

만약, $A_1$, $\cdots$, $A_n$가 $S$의 partition이고, $B$가 사건이면 다음과 같은 식이 성립합니다.

\[\begin{align*} P(A) &=P(A_1\cap A)+\cdots+P(A_n\cap A)\\ &=\sum_{i=1}^nP(A_i\cap A)\\ &=\sum_{i=1}^nP(A|A_i)P(A_i) \end{align*}\]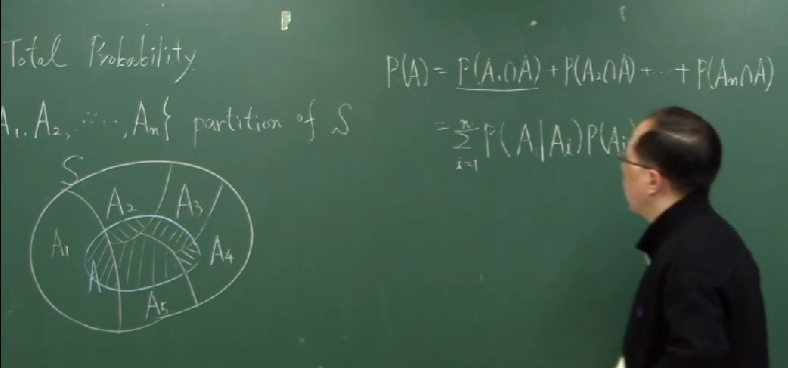

(5) Bayesian theorem

조건부확률의 식으로부터

\[P(B|A)=\frac{P(A|B)P(B)}{P(A)}\tag{$\ast$}\]

입니다. 만약 $P(B|A)$를 직접적으로 구하기가 어렵지만, $P(A_i|B)$는 구하는 것이 상대적으로 쉽고, $A_1$, $\cdots$, $A_n$이 partition을 이룰 경우에 Bayesian theorem이 자주 쓰입니다. 이때, $(\ast)$의 우변 분모인 $P(A)$는 law of total probability에 의해 구할 수 있습니다. 이것은 아래의 예를 통해 보면 확인할 수 있습니다.

Bayes theorem($\ast$)의 식의 각 항들은 다음과 같은 의미를 가지고 있습니다(출처 : 위키피디아)

• $P(B|A)$ : posterior, 사후확률
• $P(B)$ : prior, 사전확률
• $P(A|B)$ : likelihood, 우도

Bayesian theorem이 활용되는 경우는 대표적인 경우는 $P(B|A)$에서 $A$가 observation data (output)에 대응되고 $B$가 original data (input)에 대응될 때입니다. 어떤 input이 주어졌을 때 어떤 output이 나올 확률은 보통 인과관계나 선후관계를 잘 따지면 계산할 수 있지만, 어떤 output이 나왔을 때 input이 그 값으로 주어졌을 확률, 즉 반대 경우는 해석하기 어렵고 계산하기 어렵습니다. 그런 경우에 $A$와 $B$의 위치를 바꾸어서, 계산하는 트릭이 Bayesian rule입니다.

ex. 1.7 binary symmetric channel

데이터를 전송하는 어떤 기기가 transmitter와 receiver로 이루어져있다고 하겠습니다. input data와 output data가 binary인 경우에 이 구조를 binary channel이라고 한다고 합니다.

\[\begin{align*} \text{input symbols} &\in \{x_1,x_2\}&& \text{transmitter}\\ \text{output symbols} &\in \{y_1,y_2\}&& \text{receiver} \end{align*}\]

이상적인 상황은, $x_1$이 입력되었을 때 $y_1$이 잘 출력되는 경우와 $x_2$가 입력되었을 때 $y_2$가 잘 출력되는 경우입니다. 각각의 경우는 $P(y_1|x_1)$, $P(y_2|x_2)$이 큰 값으로 나타나는 경우에 해당합니다. 생각할 수 있는 네 개의 확률값들을 각각

\[\begin{align*} P_{11} = P(y_1|x_1)\\ P_{12} = P(y_2|x_1)\\ P_{21} = P(y_1|x_2)\\ P_{22} = P(y_2|x_2) \end{align*}\]

로 표기하겠습니다. (마치 행렬같습니다.)

$P(y_1|x_1)$과 같은 표현에 대한 세부적인 정의는 $\langle11\rangle$에서 다루어집니다. 여기에서는 그냥 '입력이 $x_1$일 때, 출력이 $y_1$일 확률' 정도로 이해하고 넘어가면 될 것 같습니다.

만약 $P_{11}=P_{22}$이고 $P_{12}=P_{21}$이 성립하면 이 binary channel을 binary symmetric channel이라고 부릅니다. (따라서 행렬이 symmetric한 것과는 다릅니다.) 당연히

\[\begin{align*} P_{11}+P_{21}=1\\ P_{12}+P_{22}=1 \end{align*}\]

이 성립합니다. 강의에서는 세 종류의 계산을 해보는데, 첫번째 계산은 law of total probability와 연관이 있고, 두번째와 세번째 계산은 Bayesian theorem과 연관이 있습니다.

(1) error가 발생할 확률

오류라고 판단할 수 있는 경우는 input이 $x_1$로 들어갔는데 output이 $y_2$로 나오는 경우와 그 반대(vice versa)의 경우입니다. 전자의 경우를 $\left(\{x_1\}\times S_2\right)\cap\left( S_1\times\{y_2\}\right)$로 표현해야 정확하겠지만 이것을 그냥 $x_1\cap y_2$로 쓰면

\[\begin{align*} P(\text{error}) &=P\left((x_1\cap y_2)\cup(x_2\cap y_1)\right)\\ &=P(x_1\cap y_2)+P(x_2\cap y_1)\\ &=P(y_2|x_1)P(x_1)+P(y_1|x_2)P(x_2)\\ &=P_{12}P(x_1)+P_{21}P(x_2) \end{align*}\]

라고 할 수 있습니다.

(2) When $y_2$ is received, what is the probability that $x_1$ is transmitted?

$y_2$가 출력되었을 경우에, $x_1$이 입력되었을 확률을 계산합니다. Bayes rule과 law of total probability, 그리고 $P_{ij}$의 정의에 의해

\[\begin{align*} P(x_1|y_2) &=\frac{P(y_2|x_1)P(x_1)}{P(y_2)}\\ &=\frac{P(y_2|x_1)P(x_1)}{P(y_2|x_1)P(x_1)+P(y_2|x_2)P(x_2)}\\ &=\frac{P_{12}P(x_1)}{P_{12}P(x_1)+P_{22}P(x_2)} \end{align*}\]

입니다. 여기에서 $y_2$는 아까 말한 observation data (output)이고 $x_1$은 original data (input)입니다.

(3) error가 발생했을 때, 입력값이 $x_1$이었을 확률

에러가 발생했을 때, 입력값이 $x_1$이었을 확률을 계산합니다.

\[\begin{align*} P(x_1|\text{error}) &=\frac{P(\text{error}|x_1)P(x_1)}{P(\text{error})}\\ &=\frac{P(\text{error}|x_1)P(x_1)}{P(\text{error}|x_1)P(x_1)+P(\text{error}|x_2)P(x_2)}\\ &=\frac{P(y_2|x_1)P(x_1)}{P(y_2|x_1)P(x_1)+P(y_1|x_2)P(x_2)}\\ &=\frac{P_{12}P(x_1)}{P_{12}P(x_1)+P_{21}P(x_2)}\\ &=\frac{P(x_1)}{P(x_1)+P(x_2)} \end{align*}\]

강의에서는 위 계산이 다 완성되지 않았고, 위의 계산은 나름대로 결과를 내본 것입니다. 마지막 계산에서 이 channel이 symmetric하다는 사실($P_{12}=P_{21}$)을 사용해봤습니다.

1.8 independent events

이제 사건에 대한 독립/종속을 이야기할 수 있습니다. 강의에서는 두 개의 사건 $A$, $B$에 대한 독립(independece)만을 이야기합니다. 만약 두 사건 $A$, $B$가 서로 영향을 주지 않으면, 즉

\[P(B|A)=P(B)\]

이면, 혹은

\[P(A|B)=P(A)\]

이면, 두 사건 $A$, $B$가 서로 독립이라고 말합니다. $P(A)\ne0$, $P(B)\ne0$인 경우에 이 독립조건은

\[P(A)P(B)=P(A\cap B)\tag{$\ast\ast$}\]

와 동치입니다. 강의에서는 $(\ast\ast)$를 독립의 정의로 사용하고 있습니다. 이후에 $\langle10\rangle$에서 확률변수들 간의 독립을 정의할 때에도 여전히 $(\ast\ast)$와 같은 식을 정의로서 활용합니다.

• 세 개 이상의 사건에 대한 독립을 말할 때는 mutually independent라는 용어를 씁니다.
• 독립의 개념은 독립시행(복원시행, repeated restored trial)을 다룰 때 중요합니다.
• 독립(independence)과 배반(exclusiveness)의 개념을 혼동하지 말아야 합니다.
• $A$와 $B$가 독립이면 $A$와 $\overline B$($B$의 여사건, complement)도 독립입니다.

1.9 combined experiments

For two experiments with sample spaces $S_1$ and $S_2$, the sample space of the combined experiments is the cartesian product $S_1\times S_2$;

동시에 일어나는 서로 다른 두 시행을 하나의 시행으로 보았을 때의 표본공간은, 각각의 시행에 대한 표본공간 $S_1$와 $S_2$의 cartesian product인 $S_1\times S_2$로 정의합니다.

\[S_1\times S_2=\{(x,y):x\in S_1,y\in S_2\}\]

동전 세 개를 동시에 던지는 독립시행에서, 단일 시행에 대한 표본공간은

\[S=\{H,T\}\]

이지만, combined experiments에 대한 표본공간은

\[\begin{align*} S\times S\times S &=\{H,T\}\times\{H,T\}\times\{H,T\}\\ &=\{(H,H,H),(H,H,T),(H,T,H),(H,T,T),(T,H,H),(T,H,T),(T,T,H),(T,T,T)\} \end{align*}\]

입니다.

02 독립사건과 확률

1.10 combinatorial analysis

1.10.1 permutation (순열)

서로 다른 $n$개의 대상을 일렬로 나열하는 방법의 수는

\[n!=n\times(n-1)\times\cdots\times1\]

입니다. $n!$은 $n$ factorial(팩토리얼)이라고 읽고, $0!=1$로 정의합니다.

서로 다른 $n$개의 대상 중 $r$개를 일렬로 나열하는 방법의 수는

\[_nP_r=\frac{n!}{r!}=n(n-1)\cdots(n-r+1)\]

입니다.

1.10.2 group permutation (같은 것이 포함된 순열)

세 종류의 대상 $A$, $B$, $C$가 각각 $a$개, $b$개, $c$개 있을 때($a+b+c=n$), 이 $n$개의 대상을 일렬로 나열하는 방법의 수는

\[\frac{n!}{a!b!c!}\]

입니다.

1.10.3 circular permutation (원순열)

서로 다른 $n$개의 대상을 원형으로 나열하는 방법의 수는

\[(n-1)!\]

입니다.

1.10.4 combination (조합)

서로 다른 $n$개의 대상들 중 $r$개를 선택하는 방법의 수는

\[\binom nr=_nC_r=\frac{_nP_r}{r!}=\frac{n!}{r!(n-r)!}\]

입니다. 이것은 ‘같은것이 포함된 순열’과 연관해서 설명될 수도 있습니다. 즉 $\binom nr$는 두 종류의 대상 $A$와 $B$가 각각 $r$개, $n-r$개 있을 때, 이 $n$개의 대상을 일렬로 나열하는 방법의 수와 같습니다.

1.10.4 binomial theorem (이항정리)

\[\begin{align*} (a+b)^n&=\sum_{k=0}^n\binom nka^kb^{n-k}\\ (1+x)^n&=f(x)=\sum_{k=0}^n\binom nkx^k\\ 2^n&=f(1)=\sum_{k=0}^n\binom nk\\ 0&=f(-1)=\sum_{k=0}^n(-1)^k\binom nk \end{align*}\]

이때, $\binom nk$는 $(a+b)^n$의 전개식에서 각 항의 계수(coefficient)의 역할을 한다는 점에서 이항계수(binomial coefficient)라고도 불립니다. $f(x)$를 조금 변형하면 이항분포에서의 평균과 분산 식을 계산하는 데 도움이 될 수 있습니다.

위 식의 $f(x)$를 한 번 미분하면

\[\begin{align*} n(1+x)^{n-1}=f'(x)=\sum_{k=0}^nk\binom nkx^{k-1}\\ \end{align*}\]

에서

\[\begin{equation} nx(1+x)^{n-1}=\sum_{k=0}^nk\binom nkx^k\tag{$*$} \end{equation}\]

이고 $f(x)$를 두 번 미분하여 정리하면

\[\begin{align*} n(n-1)(1+x)^{n-2}&=f''(x)=\sum_{k=0}^nk(k-1)\binom nkx^{k-2}\\ n(n-1)x^2(1+x)^{n-2}&=\sum_{k=0}^nk(k-1)\binom nkx^k \end{align*}\]

이고 마지막 식을 $(\ast)$와 더하면

\(\begin{equation}\tag{$**$} nx(1+x)^{n-2}(1+nx)=\sum_{k=0}^nk^2\binom nkx^k \end{equation}\) 입니다.

(07강에 포함되는 내용이지만) 이산확률분포 $X$가 이항분포 $B(n,p)$를 따르면, $X$의 확률질량함수는

\[P(X=k)=\binom nkp^k(1-p)^{n-k}\]

입니다. 따라서 $X$의 평균은 $(\ast)$를 사용하여

\[\begin{align*} E(X) &=\sum_{k=0}^nkP(X=k)\\ &=\sum_{k=0}^nk\binom nkp^k(1-p)^{n-k}\\ &=(1-p)^n\sum_{k=0}^nk\binom nk\left(\frac p{1-p}\right)^k\\ &\stackrel{(\ast)}=(1-p)^nn\cdot\frac p{1-p}\left(1+\frac p{1-p}\right)^{n-1}\\ &=np \end{align*}\]

으로 계산됩니다. $X$의 분산은 조금 복잡한데 $(\ast\ast)$를 사용하여

\[\begin{align*} E(X) &=E(X^2)-E(X)^2\\ &=\sum_{k=0}^nk^2P(X=k)-(np)^2\\ &=\sum_{k=0}^nk^2\binom nkp^k(1-p)^{n-k}-(np)^2\\ &=(1-p)^n\sum_{k=0}^nk^2\binom nk\left(\frac p{1-p}\right)^k-(np)^2\\ &\stackrel{(\ast\ast)}=(1-p)^n\frac{np}{1-p}\left(1+\frac p{1-p}\right)^{n-2}\left(1+\frac{np}{1-p}\right)-n^2p^2\\ &=np(1-p) \end{align*}\]

입니다. (잘 알려진 다른 증명보다 복잡한 것 같아서 유용한지는 잘 모르겠습니다.)

한편, 멱급수에 대해서도 재미있는 계산을 할 수 있습니다. 함수 $f(x)$를

\[f(x)=1+2x+3x^2+\cdots\]

로 정의하겠습니다. 이 함수가 수렴하기 위해서는 $|x|<1$라는 조건이 있어야 합니다. 양변에 $x$를 곱하면

\[xf(x)=x+2x^2+3x^3+\cdots\]

이고 두 식을 빼면

\[(1-x)f(x)=1+x+x^2+\cdots=\frac1{1-x}\]

입니다.

따라서

\[f(x)=\frac1{(1-x)^2}\]

입니다. 한편, 위의 결과를 다르게 얻을 수도 있는데

\[g(x)=1+x+x^2+\cdots\]

라고 하면 $f(x)=g’(x)$이고 $g(x)=\frac1{1-x}$이므로

\[f(x)=\left(\frac1{1-x}\right)'=\frac1{(x-1)^2}\]

인 것입니다.

1.10.6 Sterling’s formula

$n$이 충분히 크면 $n!$는 다음 값과 거의 비슷합니다.

\[\sqrt{2\pi n}\left(\frac ne\right)^n\]

강의에는 이에 대한 증명이 나와있지 않은데 이 자료(Keith Conrad의 자료)에 설명과 증명이 잘 되어 있는 것 같습니다. 여기에서의 증명은 Gaussian distribution을 통한 증명과, 어떤 함수열의 수렴을 통한 증명이 소개되고 있는 것 같습니다. (언제 한 번 이것을 공부해서 포스트로 남기면 참 좋을텐데)

엄밀한 증명은 조금 어렵지만, 대략적으로 이 식의 의미를 파악하는 건 그렇게까지 어렵지 않은 것 같습니다. 어림하고자 하는 값 $n!$에 자연로그를 취하면

\[\log(n!)=\log1+\log2+\cdots+\log n\]

인데, 이것은 정적분

\[\int_1^n\log x\,dx\]

과 관련이 있는 값입니다. 폐구간 $1\le x\le n$를 길이가 1인 $n-1$개의 구간으로 나누면, 리만적분에서 흔히 하는 방식에 의해, 정적분의 값은 $n$개의 큰 직사각형들의 넓이의 합보다는 작고 $n$개의 (사실은 $n-1$개의) 작은 직사각형들의 넓이의 합보다는 큽니다. 즉,

\[\begin{align*} \log1+\log2+\cdots+\log(n-1)&<\int_1^n\log x\,dx<\log2+\log3+\cdots+\log n\\[10pt] \log((n-1)!)&<n\log n-n+1<\log(n!)\\[10pt] n\log n-n+1&<\log(n!)<n\log n-n+1+\log n\\[10pt] e^{n\log n-n+1}&<e^{\log(n!)}<e^{n\log n-n+1+\log n}\\[10pt] e\left(\frac ne\right)^n&<n!<en\left(\frac ne\right)^n \end{align*}\]

입니다. 그러면 $n!$은 $\left(\frac ne\right)^n$이라는 값과 상당히 비슷한 값이어서

\[n!\approx\left(\frac ne\right)^n\]

라는 사실과

\[n!=g(n)\left(\frac ne\right)^n\]

와 같이 쓸 때 $e\lt g(n)\lt en$인 것도 알 수 있습니다. 그리고 실제 Sterling’s formula에서의 $g(n)=\sqrt{2\pi n}$이 위의 범위에 있는 것도 확인할 수 있습니다.

1. 11 Reliability

어떤 시스템(혹은 모듈)이 어떤 기간동안 얼마나 올바르게 고장나지 않고 잘 동작하는지를 나타내는 값을 reliability라고 합니다. 그것을 $R(t)$라고 적습니다.

series connection(직렬연결)

여러 개의 독립적인 모듈 $C_1$, $\cdots$, $C_n$ 들이 직렬로 연결되어 있고(cascade) 각 모듈들의 reliabilty가 $R_1(t)$, $\cdots$, $R_n(t)$ 이 시스템의 reliability는

\[\prod_{i=1}^nR_i(t)\]

입니다.

parallel connection(병렬연결)

이번에는 이 모듈들이 병렬로 연결되어 있다면 이 시스템의 reliability는

\[1-\prod_{i=1}^n\left(1-R_i(t)\right)\]

입니다.

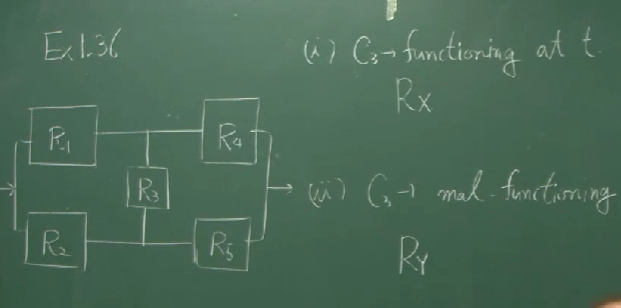
만약 위의 그림처럼 복잡한 시스템이라고 한다면, $C_3$가 동작하는지($R_x$) 동작하지 않는지($R_y$)에 따라 구분해서 얻어낼 수 있습니다. 전자의 경우에는 두 쌍의 병렬모듈들이 직렬로 연결된 것이고 후자의 경우에는 두 쌍의 직렬모듈들이 병렬로 연결된 것이라고 볼 수 있습니다.

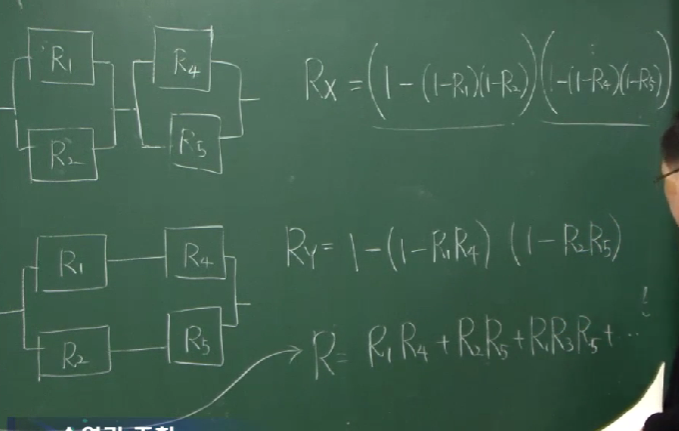
따라서

\[\begin{align*} R =&R_x+R_y\\ =&R_3\left[\left(1-(1-R_1)(1-R_2)\right)\left(1-(1-R_4)(1-R_5)\right)\right]\\ &+(1-R_3)\left[1-(1-R_1R_4)(1-R_2R_5)\right] \end{align*}\]

입니다.

03 확률변수의 정의

Chapter 2. Random Variables(확률변수)

2.2 definition of random variables

언제나 확률변수의 개념을 정확히 이해하는 건 쉬운 일은 아닌 것 같습니다. 한 번 볼 때마다 완벽히 이해한다고 생각하지만, 어찌된 것인지 볼때마다 새로운 것 같습니다. 그래도 다시 한 번 강의를 보며 다시 한 번 이해해봤습니다.

확률변수란, 어떤 시행의 근원사건 $w\in S$을 하나의 실수 $X(w)$로 대응시키는 함수 $X$를 말합니다. 다시 말해, $X$가 확률변수이면, $X$는 $X:S\to\mathbb R$인 함수를 말합니다.

A random variable is a function $X$ mapping each outcome of random experiment $w\in S$ to a real number $x=X(w)$.

ex.1 : tossing a coin

동전을 하나 던져서 앞면이 나오면 1점을 얻고 뒷면이 나오면 $0$점을 얻는 어떤 시행에서,

동전을 하나 던졌을 때 얻는 점수

를 확률변수 $X$로 정의할 수 있습니다. 이 시행에서 $S=\{H,T\}$이고, 확률변수 $X$는 $S$에서 $\mathbb R$로 가는 함수로서

\[\begin{align*} X(H)&=1\\ X(T)&=0 \end{align*}\]

를 만족하는 함수입니다. 확률변수를 사용하면 확률 $P(~\cdot~)$를 마치 숫자들의 함수로서 생각할 수 있게 됩니다. 그전까지 $P(A)$라는 표현에서 $A$는 사건(event)이라고 불렸고 표본공간 $S$의 부분집합을 의미했습니다. 그러니까 그전까지는 확률 $P(~\cdot~)$가 마치 ‘집합의 함수’처럼 동작했습니다. 그래서

\[P(\{H\})=\frac12,\quad P(\{T\})=\frac12,\quad P(\varnothing)=0,\quad P(S)=1\]

와 같은 표현들을 사용할 수 있었지만 직관적인 표현은 아니었습니다.

그런데 확률변수 $X$를 도입하고 나면 $P(~\cdot~)$를 숫자들의 함수처럼 생각할 수 있습니다. $p(x)$ 혹은 $P(X=x)$라는 표현을 (이것들은 나중에 확률질량함수라는 이름을 가지게 되는데)

\[\begin{align*} p(x) &=P(X=x)\\ &=P\left(\{w\in S:X(w) =x\}\right)\tag{$\ast$} \end{align*}\]

와 같이 정의하면

\[\begin{align*} p(1)&=P(X=1)=\frac12\\ p(0)&=P(X=0)=\frac12 \end{align*}\]

와 같이 쓸 수 있습니다. $P$는 집합을 숫자로 대응시키는, 조금 복잡한 느낌이었지만 $p$는 숫자를 숫자로 대응시키고 있어서 다루고 이해하기가 편합니다.

ex.2 : tossing two coins

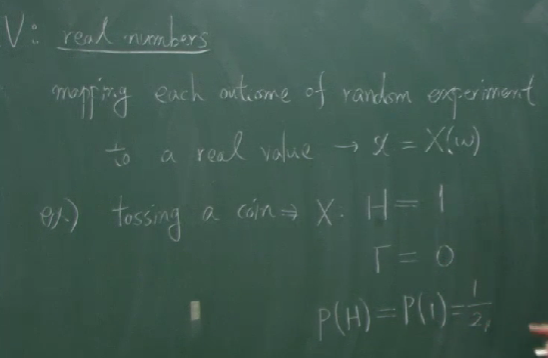
이번에는 동전던지기에 관한 또다른 확률변수를 생각해봅니다.

동전을 두 번 던졌을 때 나온 앞면의 수

도 확률변수 $X$가 됩니다. 이때의 표본공간은

\[\begin{align*} S &=\{H,T\}^2\\ &=\{(H,H),(H,T),(T,H),(T,T)\} \end{align*}\]

인데, 강의에서는 cartesian product에서의 순서쌍의 표현을 생략하여, $S=\{HH,HT,TH,TT\}$로 쓰고 있습니다. 확률변수 $X$는

\[\begin{align*} X(HH)&=2\\ X(HT)&=1\\ X(TH)&=1\\ X(TT)&=0 \end{align*}\]

로 정의되고 기존의 확률의 정의로는

\[\begin{align*} P(\{HH\})&=\frac14\\ P(\{HT,TH\})&=\frac12\\ P(\varnothing)&=0\\ P(S)&=1 \end{align*}\]

와 같은 표현을 사용할 수 있었습니다. 그런데 이것을 확률변수의 함수로서 쓰면

\[\begin{align*} p(0)&=P(X=0)=\frac14\\ p(1)&=P(X=1)=\frac12\\ p(2)&=P(X=2)=\frac14 \end{align*}\]

이 됩니다.

관습적으로 확률변수 자체는 대문자 기호 $X$, $Y$, $Z$ 등으로, 확률변수가 가지는 특정한 값은 $x$, $y$, $z$ 등으로 나타냅니다.

2.3 events defined by RV

강의에서는 $A_x$를 도입해서 설명하고 있습니다. 이때 $A_x$는 사건으로서, 확률변수 $X$가 $x$의 값을 가지는 경우, 즉 $X(w)=x$인 $w\in S$들의 집합으로, 아까 $(\ast)$에서 $p(x)$ 혹은 $P(X=x)$를 정의할 때 쓰인 집합입니다.

\[\begin{align*} A_x &=\{w\in S:X(w)=x\}\\ &=X^{-1}(\{x\}) \end{align*}\]

따라서,

\[p(x)=P(X=x)=P(A_x)\]

입니다.

지금까지, $P(~\cdot~)$에 들어가는 것이 사건(event, $S$의 부분집합)이었던 것을, 특정한 숫자로 들어갈 수 있게 바꾸었습니다. 여기에는 ‘숫자들의 집합’도 들어갈 수 있습니다. 예를 들어 $\{X:a\lt X\le b\}$와 같은 집합도 들어갈 수 있습니다. 보통 쓸 때는 $P(\{X:a\lt X\le b\})$로 쓰지 않고 $P(a\le X\le b)$로 표기하는데

\[P(a<X\le b)=P\left(\{w\in S:a<X(w)\le b\}\right)\]

의 의미입니다. 예를 들어, 동전 두 개를 던지는 시행에서

\[P(X\le1)=P\left(\{HH,HT,TH\}\right)=\frac34\]

입니다.

2.4 distribution functions

확률변수 $X$와 실수 $x$에 대하여 cumulative distribution function(CDF, 누적확률함수)은

\[F_X(x)=P\left(X\le x\right)\]

로 정의합니다. 위의 동전 두 개를 던지는 시행에서

\[F_X(1)=\frac34\]

였습니다.

따라서 CDF는

• nondecreasing 입니다 : if $x_1\lt x_2$, then $F_X(x_1)\le F_X(x_2)$
• 치역이 $[0,1]$입니다 : $0\le F_X(x)\le1$
• 두 점근선을 가집니다 : $\displaystyle\lim_{x\to\infty}F_X(x)=1$, $\displaystyle\lim_{x\to-\infty}F_X(x)=0$
• $P(a\lt X\le b)=F_X(b)-F_X(a)$
• $P(x>a)=1-F_X(a)$

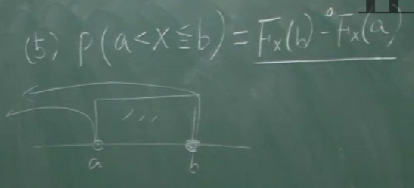
위의 $P(a\lt X\le b)$에서와 같이 부등호를 $\lt$로 할지 $\le$로 할지는 잘 구분해주어야 합니다. 다만, 연속확률변수의 경우에는 (아래 예제와 같은 예외가 발생하지 않는 한은) 둘 사이에 구분을 두지 않아도 됩니다.

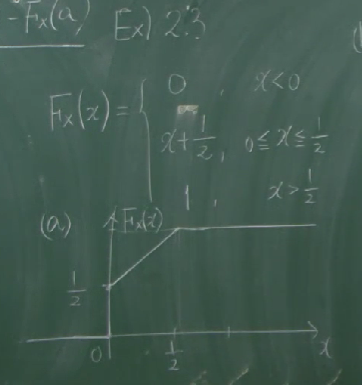
위 그림과 같은 예제에서 CDF는

\[F_X(x)=\begin{cases} 0&(x\lt0)\\ x+\frac12&(0\le x\le\frac12)\\ 1&(x\gt\frac12)\\ \end{cases}\]

와 같이 주어져 있는데

\[\begin{align*} P\left(X>\frac14\right)&=1-F_X\left(\frac14\right)=1-\frac34=\frac14\\ P(X>0)&=1-F_X(0)=1-\frac12=\frac12\\[10pt] P(X\ge0)&=1\\[10pt] P(X=0)&=1\\[10pt] P\left(X\ge\frac14\right)&=\frac14 \end{align*}\]

입니다. 아래의 세 개 계산은 nontrivial합니다. 좌우극한을 가지고 계산하면

\[\begin{align*} P(X\ge0) &=1-P(X\lt0)\\[10pt] &=1-\lim_{x\to0-}P(X\le x)\\ &=1-0=1\\[10pt] P(X=0) &=P(X\le0)-P(X\lt0)\\ &=\frac12-0=1\\ P\left(X\ge\frac14\right) &=1-P\left(X\lt\frac14\right)\\[10pt] &=1-\lim_{x\to\frac14-}P(X\le x)\\ &=1-\lim_{x\to\frac14-}\left(x+\frac12\right)\\ &=1-\frac34=\frac14 \end{align*}\]

입니다. 이때, $P(X>\frac14)=P(X\ge\frac14)$이지만 $P(X>0)=P(X\ge0)$인 것은 $F_X(x)$가 $x=\frac14$에서는 연속이지만 $x=0$에서는 불연속인 사실과 관련이 있습니다.

2.5 discrete random variables(이산확률변수)

확률변수 $X$가 가질 수 있는 값이 유한개이면 (혹은 countable개이면) $X$를 이산확률변수라고 부릅니다. 이 때, 확률질량함수(probability mass function, PMF) $P_X(x)$를 다음과 같이 정의합니다.

\[P_X(x)=P(X=x)\]

예를 들어, 동전을 두 개 던져 앞면이 나온 횟수를 $X$라고 할 때

\[\begin{align*} P_X(0)=\frac14\\ P_X(1)=\frac12\\ P_X(2)=\frac14 \end{align*}\]

입니다. PMF와 CDF 사이의 관계는 다음과 같습니다.

\[F_X(x)=\sum_{x_i\le x}P_X(x_i)\]

이산확률변수의 분포(distribution)는 확률질량함수의 그래프로서 나타내는데, 그것을 $xy$ 평면에 찍힌 여러 개의 점으로 표현하기보다는, 여러 개의 선분으로써 표현하는 경향이 있는 것 같습니다.

동전을 두 개 던지는 시행에서의 확률질량함수의 그래프와 CDF와 PMF의 그래프는 아래와 같습니다. CDF의 그래프는 step function으로 나타나는 것을 볼 수 있습니다.

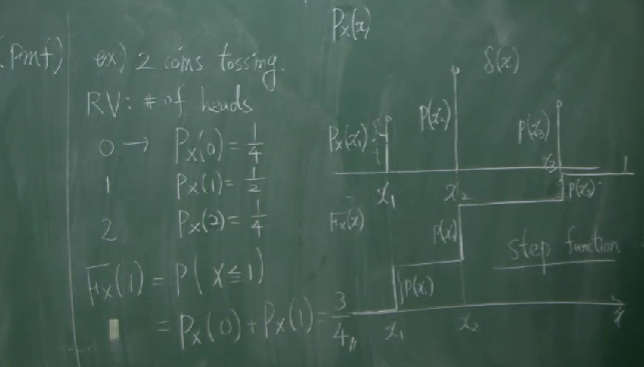
dirac delta function

$\langle04\rangle$에서 연속확률변수를 다루게 됩니다. 그리고, 연속확률변수에서는 확률질량함수(PMF)가 아닌 확률밀도함수(PDF)를 다루게 됩니다.

이산확률변수 $X$에 대해서도 확률밀도함수 $f_X(x)$를 생각할 수 있을까?

에 대한 답은 특별한 함수 $\delta$에서 찾을 수 있습니다.

강의에서는 $\delta$함수에 대해 간단하게만 언급하고 있는데, 포스트에서는 위키피디아 등을 참고하여 조금 더 적어보았습니다.

다시 말해, 연속확률변수에서는

\[P(a\lt X\le b)=\int_a^bf_X(x)\,dx\]

와 같은 식을 만족시키는 함수 $f_X(x)$를 생각하게 되는데, 확률질량함수 $P_X(x)$의 그래프에서는 ‘그래프 아래의 면적’이라는 개념을 정의할 수 없으니까 애매합니다. 그럴 때에, 함수 $\delta$(dirac delta function)를 도입하는데, 이 함수는

\[\delta(x)\approx \begin{cases} +\infty&(x=0)\\ 0&(x\ne0) \end{cases}\]

와 같이 정의됩니다. 이 함수는 $x\ne0$인 곳에서는 함숫값이 0이고 $x=0$인 곳에서만 함숫값이 $\infty$인 불연속함수처럼 적혀있는데, 실제로는 연속함수처럼 생각합니다. 또, 실수 전체의 범위에서 적분했을 때의 값이 $1$인 것으로 가정합니다.

\[\int_{-\infty}^{\infty}\delta(x)\,dx=1\]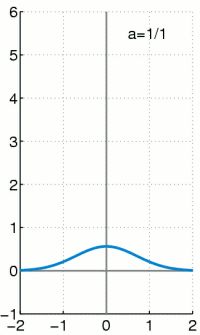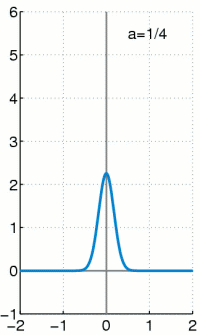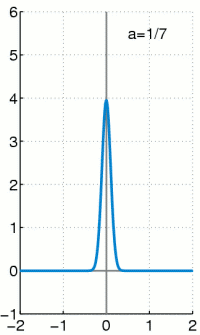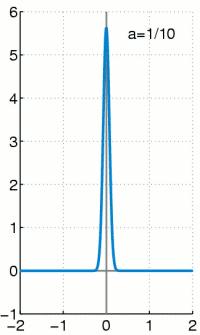

따라서 이 함수 $\delta(x)$가

\[P_X(x)= \begin{cases} 1&(x=0)\\ 0&(x\ne0) \end{cases}\]

와 같이 정의된 가장 기본적인 확률질량함수 $P_X(x)$에 대응되는 확률밀도함수라고 생각할 수 있습니다. 일반적인 확률질량함수에 대한 확률밀도함수는 이 $\delta(x)$를 적절히 shift($x$축방향의 평행이동)한 것들을 가지고 일차결합하여 만들어낼 수 있습니다. 즉

\[P_X(x)= \begin{cases} p_1&(x=x_1)\\ &\vdots\\ p_n&(x=x_n) \end{cases}\]

인 확률질량함수 $P_X(x)$에 대해서 (단, $p_1+\cdots+p_n=1$)

\[f_X(x)=\sum_{k=1}^np_k\delta(x-x_k)\]

가 확률밀도함수의 역할을 할 수 있습니다.

예를 들어, 동전을 두 번 던지는 시행에 대해서는 PDF를

\[f_X(x)=\frac14\delta(x)+\frac12\delta(x-1)+\frac14\delta(x-2)\]

로 정할 수 있습니다.

dirac delta function은 엄밀히 말하면 함수가 아닌 generalized function이며, measure나 distribution을 통해 이해될 수 있다고 합니다.

04 이산확률변수와 연속확률변수

2.6 continuous random variables

앞서 강의에서 확률변수를 $X:S\to\mathbb R$인 함수로 정의했습니다. 어떤 확률변수가 이산확률변수인지 연속확률변수인지를 결정하는 것은 이 확률변수의 치역 $X(S)$과 관련이 있습니다. $X(S)$가 countable이면 (혹은 at most countable, 그러니까, finite이거나 countably infinte) $X$를 이산확률변수라고 합니다. 이것은

확률변수 $X$가 가질 수 있는 값이 유한개(혹은 countable)이면 $X$를 이산확률변수라고 부릅니다.

와 같은 앞서의 정의를 다시 쓴 것입니다.

만약, 확률변수가 이산확률변수가 아니면 연속확률변수라고 부릅니다. 그러니까, 치역 $X(S)$가 uncountable인 경우를 말합니다. 말로 풀어 쓰면

확률변수 $X$가 가질 수 있는 값이 uncountable하게 많으면 $X$를 연속확률변수라고 부릅니다.

이산확률분포의 경우에 비해 연속확률분포의 경우에는 조금 어렵고 섬세한 이야기들이 많이 산적해있습니다. 예를 들어 0과 1 사이의 숫자를 임의로 뽑을 때 그 값을 $X$라고 하면, $X$는 연속확률변수입니다. 그런데 이런 경우에 $P(X=0.5)$을 어떻게 정의해야 할 지 애매합니다.

답 : $P(X=0.5)=0$
확률을 measure-theoretic하게 생각하면 $P$는 하나의 measure라고 볼 수 있고 이 경우에는 '집합의 길이'와 관련된 measure를 $P$로써 정의합니다. 그런데 원소가 하나인 집합에 대한 '길이'는 0이므로 $P(X=0.5)=0$입니다.
조금 다르게 설명할 수도 있습니다. $P(X=0.5)=a$로 두면 ($a>0$) 다른 모든 숫자 $0\le x\le1$에 대해서도 마찬가지로 $P(X=x)=a$가 성립한다고 말할 수 있을 겁니다. 그러면, 모든 $x$에 대하여 이 확률값들을 더했을 때 1이 되어야 합니다. 사실 이 덧셈이 잘 정의되는지도 의문이기는 하지만, 어쨌든 양수 $a$를 무한번 더해서 1이 된다는 것인데, 이건 말이 안됩니다. 따라서, 임의의 양의 실수 $a$에 대하여 $P(X=0.5)=a$인 것은 불가능하고, 따라서 $P(X=0.5)=0$일 수밖에 없습니다.

즉, 연속확률변수에서는 PMF가 잘 작동하지 않고, 따라서 다른 방식으로 연속확률분포를 이해할 필요가 있습니다. 강의에서는 다음과 같은 영어 문장으로 이 문제를 표현하고 있습니다.

It is not possible to define a probability value for each $x$.

$X$가 특정한 값 $x$를 가질 때의 확률은 정의하기 어려운 데 비해, $X$가 어떤 구간 안에 위치할 확률은 많은 경우에 계산할 수 있습니다. 예를 들어, 0과 1 사이의 숫자를 임의로 뽑을 때, 그 수가 0.1과 0.3사이의 값을 가질 확률은 0.2이라고 생각할 수 있습니다. 왜냐하면, $S$의 길이는 1인데 비해 $[0.1,0.3]$의 길이는 0.2이기 때문입니다.

\[P(0.1\lt X\lt 0.3)=\frac{0.2}1=0.2\]

그러니까, 특정한 점 $X=x$에 대한 확률(확률질량함수)을 정의하는 대신 $x$를 포함하는 infinitesimal한 구간을 생각하고 그 구간에 대한 확률값을 그 구간의 길이로 나눈 값을 고려할 수 있습니다. 그리고 그 값은 $F_X$가 미분가능할 경우 $F_X$의 $x$에서의 미분계수와 정확히 일치합니다.

\[\begin{align*} f_X(x) &=\lim_{\Delta x\to0+}\frac{P\left(x<X\le x+\Delta x\right)}{\Delta x}\\ &=\lim_{\Delta x\to0+}\frac{F_X(x+\Delta x)-F_X(x)}{\Delta x}\\ &=F_X'(x) \end{align*}\]

이 함수 $f_X(x)$를 확률밀도함수(probability density function)이라고 부릅니다. 위의 식은 CDF가 주어졌을 때 PDF를 구하는 방법이기도 합니다. 반대로, PDF가 주어졌을 때 CDF를 구하려면, $f_X=F_X’$와 $\displaystyle\lim_{x\to-\infty}F_X(x)=0$로부터

\[F_X(x)=\int_{-\infty}^xf_X(\tilde x)\,d\tilde x\]

와 같이 구할 수 있습니다.

CDF는 일반적으로 미분가능하지 않을 수도 있지만, 이 강의에서는 CDF가 미분가능한 경우만 다룬다고 합니다. CDF가 미분가능하지도 않고, 심지어 불연속인 극단적인 경우는 2.3에서 봤었습니다.

함수 $f_X(x)$가 어떤 연속확률변수의 PDF이기 위해서는 다음 두 조건을 만족시켜야 합니다.

(1) $f_X(x)\ge0$

(2) $\int_{-\infty}^\infty f_X(x)\,dx=1$

마찬가지로, 함수 $P_X(x)$가 어떤 이산확률변수의 PMF이기 위해서는 다음의 두 조건을 만족시켜야 합니다.

(1’) $P_X(x_i)\ge0$

(2’) $\sum_{k=1}^nP_X(x_i)=1$

PDF의 추가적인 성질들은 다음과 같습니다.

(3) $\int_a^bf_X(x)\,dx=P(a\lt X\le b)$

이것은, 지금까지 쓴 개념들을 동원해 쉽게 증명됩니다.

\[\begin{align*} P(a\lt X\le b) &=F_X(b)-F_X(a)\\ &=\int_{-\infty}^bf_X(x)\,dx-\int_{-\infty}^af_X(x)\,dx\\ &=\int_a^bf_X(x)\,dx \end{align*}\]

(4) $P(X\lt a)=P(X\le a)$

만약, 임의의 실수 $a$에 대하여 $P(X=a)=0$가 항상 성립한다고 가정할 때, (4)는 당연합니다. 왜냐하면

\[P(X\le a)=P(X\lt a)+P(X=a)=P(X\lt a)+0=P(X\lt a)\]

이기 때문입니다.

위의 (4)번식은 성립하는 여러 식들 중 하나를 대표적으로 쓴 것입니다. 일반적으로, 연속확률변수의 확률표현식에서 $\le$와 $\lt$는 적절히 바꿔가면서 사용될 수 있습니다.

ex 2.11

$0\lt x\lt 2$에 대하여 $f_X(x)=A(2x-x^2)$이 PDF가 되려면

\[1 =A\int_0^22x-x^2\,dx =\frac43A\]

으로부터 $A=\frac34$입니다.

ex 2.15 uniform distribution

$f_X(x)$가 (혹은 $P_X(x)$가) 상수함수이면 $X$가 uniform distribution을 따른다고 정의합니다. 아까, 0과 1 사이의 숫자를 임의로 골라 그 값을 $X$라고 할때, $X$는 uniform distribution을 따릅니다. 주사위를 하나 던져 눈을 보는 것도 일종의 uniform distribution에 해당합니다.

고등학교 과정의 ‘기하학적 확률’에서 확률을 넓이 혹은 길이에 의존해 계산하게 되는데 그러한 상황 또한 uniform distribution을 가정하고 있습니다.

강의의 마지막 부분에는 신호나 그림에서의 sampling과 quantization, binarization에 대해 언급됩니다. (아래 캡쳐)

이에 대한 설명은 다음과 같습니다.

연속적인 아날로그 신호(continuous, analogue signal)를 특정한 주파수로 sampling하면 discrete signal을 얻을 수 있습니다. 이 discrete signal을 표현할 때에는 특정한 step size를 가정하여 level의 형태로 얻게 되는데 이 과정을 양자화(quantization)라고 부릅니다. 마지막으로 이 값들을 2진수로 바꾸어(binarization) 디지털 신호로 바꾸는 과정이 있습니다. 이 일련의 과정들은 아날로그로 주어진 데이터를 디지털의 형태로 바꾸는 작업입니다. 이때, 실제 신호와 level로 주어진 근사값들 사이의 차이를 quantization error라고 가정하는데, 많은 경우에 이 error를 uniform distribution을 따른다고 가정하고 모델링을 진행한다고 합니다.

확률분포(probabilistic distribution)
확률변수 $X$가 어디에 얼마나 분포되어있는지 하는 것을 그 확률변수의 분포(distribution)이라고 합니다. 이 분포를 직접적으로 표현하는 것이 PMF(확률질량함수, probability mass function), PDF(확률밀도함수, probability density function), CDF(누적분포함수, cumulative distribution function)와 같은 분포함수들입니다. 그 중 이산확률변수에 대해서는 PMF를, 연속확률분포에 대해서는 PDF를 주로 분포함수로 취급하게 되는데 PMF와 PDF는 모든 종류의 확률변수에 대해 잘 정의되지 않습니다.
예를 들어, PDF로는 이산확률분포를 정하기가 힘들었습니다. 그래프의 면적이 1이 된다는 점을 만족시키기 위해서 dirac delta function 같은 것을 도입해야 했습니다. 또, PMF로는 연속확률분포를 정하는 데 어려움이 있었습니다. 각 점에 대한 PMF의 값이 0이 될 수밖에 없는데, 그건 그것대로 모순이었습니다.
하지만, CDF는 $X$가 이산확률변수이건 연속확률변수이건 상관없이 적절하게 잘 정의될 수 있습니다. 또한, 일단 CDF가 정해지고 나면 CDF의 식으로부터 PMF나 PDF의 식을 쉽게 구할 수 있다는 점도 있습니다. 그래서 그런지, 많은 경우에 CDF를 먼저 정의하고, 그 이후에 PMF나 PDF를 정의하는 것 같습니다.

05 확률변수의 평균과 분산

Chapter 3. Moments of Random Variables

arithemetic average(산술평균)

$x_i$들의 산술평균은

\[\bar x=\frac{x_1+\cdots+x_N}N.\]

different frequences

서로다른 $x_i$들에 대하여 그 빈도 $w_i$가 주어져 있을 때의 가중평균(weighted average)은

\[\bar x=\frac{w_1x_1+\cdots+w_Nx_N}{w_1+\cdots+w_N}.\]

3.1 expectation(mean)

\[\begin{align*} E[X]&=\sum_{i=1}^nx_iP_X(x_i) &&(\text{discrete})\\ E[X]&=\int_{-\infty}^\infty xf_X(x)\,dx &&(\text{continuous}) \end{align*}\]

ex 3.3 Poisson distribution

이산확률변수 $K$가 다음과 같은 확률질량함수를 가지고 있으면, $K$가 Poisson distribution을 따른다고 말합니다.

\[P_K(k)=\frac{\lambda^k}{k!}e^{-\lambda}\qquad(k=0,1,2,\cdots)\]

Poisson distribution의 자세한 의미에 대해서는 $\langle08\rangle$에 적어보았습니다. 그래도 간단히 요약하면,

단위시간동안 평균적으로 $\lambda$번의 사건이 일어난다고 기대될 때, 단위시간동안 사건이 일어난 횟수

를 $K$라고 하면, $K$는 위의 PMF를 가집니다. 이에 대한 증명은 $\langle08\rangle$에서 해보았습니다.

$P_K$가 PMF가 되기 위해서는 두 조건을 만족시켜야 하는데 첫번째 조건인 $P_K(k)\ge0$은 당연합니다. 두번째 조건인 $\sum_k P_K(k)=1$을 위해서는 $e^x$에 대한 Maclaurin series(혹은 지수함수에 대한 추상적인 정의)를 사용할 수 있습니다;

\[e^x=\sum_{k=0}^\infty\frac{x^k}{k!}\]

여기에 $x=\lambda$를 대입하여

\[e^\lambda=\sum_{k=0}^\infty\frac{\lambda^k}{k!}\]

를 얻습니다. 이 식의 양변에 $e^{-\lambda}$를 곱하면

\(1=\sum_{k=0}^\infty\frac{\lambda^k}{k!}e^{-\lambda}=\sum_{k=1}^\infty P_K(k)\) 가 되어 두번째 조건을 만족시킵니다. 따라서 $P_K(k)$는 정말로 PMF가 됩니다. 강의에서는 일반적인 Taylor series에 대한 설명도 포함되어 있습니다.

이 Poisson distribution에 대한 평균을 구해보면

\[\begin{align*} E[X] &=\sum_{k=0}^\infty kf_K(k)\\ &=\sum_{k=0}^\infty k\frac{\lambda^k}{k!}e^{-\lambda}\\ &=\sum_{k=1}^\infty k\frac{\lambda^k}{k!}e^{-\lambda}\\ &=\lambda\sum_{k=1}^\infty\frac{\lambda^{k-1}}{(k-1)!}e^{-\lambda}\\ &=\lambda\sum_{m=0}^\infty\frac{\lambda^m}{m!}e^{-\lambda}\\ &=\lambda \end{align*}\]

이 됩니다.

확률질량함수가 $$ P_K(k)=\frac{\lambda^k}{k!}e^{-\lambda}\qquad(k=0,1,2,\cdots) $$ 인 Poisson distribution을 표현할 때, $\lambda$의 의미를 강조하기 위하여 $K$가 평균이 $\lambda$인 Poisson distribution을 따른다 라고 말하기도 합니다. 그리고 기호로는 $$K\sim\text{Pois}(\lambda)$$ 로 표현합니다.

ex 3.4 exponential distribution

연속확률변수 $X$가 다음과 같은 확률밀도함수를 가지고 있으면, $X$가 exponential distribution을 따른다고 말합니다.

\[\begin{align*} f_X(x)= \begin{cases} \lambda e^{-\lambda x} &x\ge0\\ 0 &x\lt0 \end{cases} \end{align*}\]

이번에도, exponential distribution의 자세한 의미에 대해서는 $\langle08\rangle$에서 다시 설명하겠습니다. 그래도 간단히 요약하면,

단위시간동안 평균적으로 $\lambda$번의 사건이 일어난다고 기대될 때, 사건이 발생하기까지의 시간

를 $X$라고 하면, $X$는 위의 PDF를 가집니다. 이에 대한 증명은 $\langle08\rangle$에서 해보았습니다.

이번에도 $f_X$가 PDF가 되기 위해서는 두 가지 조건을 만족시켜야 하는데 첫번째 조건 $f_X(x)\ge0$은 당연합니다. 두 번째 조건인 $\int_{-\infty}^\infty f_X(x)\,dx=1$ 을 확인해보면

\[\begin{align*} \int_{-\infty}^\infty f_X(x)\,dx &=\lambda\int_0^\infty e^{-\lambda x}\,dx\\ &=\lambda\times\left[-\frac1\lambda e^{-\lambda x}\right]_0^\infty\\ &=\lambda\times\frac1\lambda\\ &=1 \end{align*}\]

이 성립합니다. 한편, 평균을 구해보면

\[\begin{align*} E[X] &=\int_{-\infty}^\infty xP_X(x)\,dx\\ &=\lambda\int_0^\infty xe^{-\lambda x}\,dx\\ &=\lambda\left(\left[-\frac1\lambda xe^{-\lambda x}\right]_0^\infty +\int_0^\infty\frac1\lambda e^{-\lambda x}\,dx\right)\\ &=\lambda\left(0+\left[-\frac1{\lambda^2}e^{-\lambda x}\right]_0^\infty\right)\\ &=\frac1\lambda \end{align*}\]

입니다. 세번째 등호에서 부분적분을 사용했습니다.

(a) 이와 같은 푸아송 분포와 지수분포는 특정한 값(parameter) $\lambda$에 의존합니다. 실제 자연현상이나 사회현상은 그 분포를 알 수 없는데, 우리는 특정한 확률모델을 전제하여 그 현상을 모델링해볼 수 있습니다. 이와 같은 과정을 parametric estimation (혹은 parametric probability density estimation) 이라고 부르는 것 같습니다.
(b) 연속확률변수 $X$가 $$f_X(x)= \begin{cases} \lambda e^{-\lambda x} &x\ge0\\ 0 &x\lt0 \end{cases} $$ 를 그 밀도함수로 가질 때 $$X\sim\text{Exp}(\lambda)$$ 로 표현하기도 합니다.

3.4 moments of random variables

nth order moments

\[\begin{align*} E[X^n]&=\sum_i{x_i}^n P_X(x_i)&&(\text{discrete})\\ E[X^n]&=\int_{-\infty}^\infty x^n f_X(x)\,dx&&(\text{continuous}) \end{align*}\]

central moments

\[\begin{align*} E[(X-\mu)^n]&=\sum_i(x_i-\mu)^nP_X(x_i)&&(\text{discrete})\\ E[(X-\mu)^n]&=\int_{-\infty}^\infty(x-\mu)^n f_X(x)\,dx&&(\text{continuous}) \end{align*}\]

$n=1$이면

\[\begin{align*} E[(X-\mu)] &=\sum_i(x_i-\mu)P_X(x_i)\\ &=\sum_ix_iP_X(x_i)-\mu\sum_iP_X(x_i)\\ &=\mu-\mu\times 1\\ &=0 \end{align*}\]

이고

\[\begin{align*} E[(X-\mu)] &=\int_{-\infty}^\infty(x-\mu)f_X(x)\,dx\\ &=\int_{-\infty}^\infty xf_X(x)\,dx-\int_{-\infty}^\infty \mu f_X(x)\,dx\\ &=E[X]-\mu\times1\\ &=0 \end{align*}\]

입니다. 즉, 편차의 합은 항상 0입니다.

$n=2$이면

\[\begin{align*} E[(X-\mu)^2] &=\sum_i(x_i-\mu)^2P_X(x_i) \end{align*}\]

인데 이 값을 분산(variance)이라고 부르고 ${\sigma_X}^2$으로 씁니다. 강의에서는 ${\sigma_X}^2$와 같은 표현만 쓰이고 있지만, 이 포스트에서는 $V[X]$와 같은 표현도 종종 사용하겠습니다. 분산에 관한 성질은 다음과 같습니다.

• 분산은 항상 0보다 크거나 같습니다.
• uniform distribution의 분산은 0이고 그 역도 성립합니다.
• 분산이 작으면 변량들이 평균에 모여있고 분산이 크면 변량들이 넓게 분포되어 있습니다.
• $t$에 대한 함수 $g(t)=E[(X-t)^2]$를 생각하면 이 함수는 $t=\mu$에서 최솟값 ${\sigma_X}^2$를 가집니다.

LOTUS : law of the unconscious statistician
$\langle14\rangle$ 다루게 되겠지만, 여기에서 미리 말해놓는 게 좋을 것 같습니다. 흔히 LOTUS라는 약칭으로 불리는 정리 혹은 정의로서, 함수 $g$에 대하여 $g(X)$의 평균을 구하는 식이 있습니다 ; $$ \begin{align*} E[g(X)]&=\sum_ig(x_i)P_X(x_i) &&(\text{discrete})\\ E[g(X)]&=\int_{-\infty}^\infty g(x)f_X(x)\,dx &&(\text{continuous}) \end{align*}\tag{LOTUS, $\ast$} $$ 아까 평균에 대해 정의한 것은 $$ \begin{align*} E[X]&=\sum_{i=1}^nx_iP_X(x_i) &&(\text{discrete})\\ E[X]&=\int_{-\infty}^\infty xf_X(x)\,dx &&(\text{continuous}) \end{align*}\tag{$\ast\ast$} $$ 와 같은 정의가 전부였습니다. 그런데 무의식적(unconscious)으로 $$ \begin{align*} E[X^n]&=\sum_i{x_i}^n P_X(x_i)&&(\text{discrete})\\ E[X^n]&=\int_{-\infty}^\infty x^n f_X(x)\,dx&&(\text{continuous}) \end{align*} $$ 와 같은 계산을 했습니다. 이 계산이 정당화되려면 LOTUS와 같은 식을 먼저 증명해야 하는 것입니다. 통계학자들은 보통 이와 같은 논리적인 비약을 알아차리지도 못한 채로 논의를 진행시킨다는 의미에서, 이 정리는 law of the unconscious statistician라는 이름으로 불립니다.
결론부터 말하자면, LOTUS의 식 $(\ast)$은 성립합니다. 다만, 그 증명이 아주 당연하지는 않습니다. discrete case는 증명이 쉽지만, continuous case에 대한 일반적인 증명은 어렵습니다. 그래서, $(\ast\ast)$를 정의로, LOTUS를 정리로 두고 그것의 증명을 시도하는 대신, LOTUS의 식 $(\ast)$을 정의로서 차용하는 경우도 있다고 합니다. 이렇게 평균을 LOTUS의 식으로 정의해버리면, 기존 정의와도 일치하는 정의가 되면서, 굳이 어려운 증명을 하지 않아도 되게 됩니다.
이 포스트에서는 $(\ast\ast)$를 정의로 두고 LOTUS를 증명하려고 합니다. 그것들은 $\langle14\rangle$에서 다시 다루겠습니다. 다만, LOTUS를 아직 비록 증명하지는 않았더라도, LOTUS는 앞으로 사용할 예정입니다.

Proposition 3.3

어떤 확률변수 $X$에 대한 함수 $g_1(X)$, $g_2(X)$와 실수 $a_1$, $a_2$에 대하여

\[E[a_1g_1(X)+a_2g_2(X)]=a_1E[g_1(X)]+a_2E[g_2(X)]\]

이 성립합니다. LOTUS 식에 넣으면 바로 증명됩니다. 만약 $X$가 이산확률변수이면

\[\begin{align*} E[a_1g_1(X)+a_2g_2(X)] &=\sum_i\left(a_1g_1(x_i)+a_2g_2(x_i)\right)P_X(x_i)\\ &=a_1\sum_ig_1(x_i)P_X(x_i)+a_2\sum_ig_2(x_i)P_X(x_i)\\ &=a_1E[g_1(X)]+a_2E[g_2(X)] \end{align*}\]

이고, 만약 $X$가 연속확률변수이면

\[\begin{align*} E[a_1g_1(X)+a_2g_2(X)] &=\int_{-\infty}^\infty\left(a_1g_1(x)+a_2g_2(x)\right)f_X(x)\,dx\\ &=a_1\int_{-\infty}^\infty g_1(x)f_X(x)\,dx +a_2\int_{-\infty}^\infty g_2(x)f_X(x)\,dx\\ &=a_1E[g_1(X)]+a_2E[g_2(X)] \end{align*}\]

이기 때문입니다.

이것은 $E$가 linear operator라는 뜻입니다. 즉, 모든 실함수(혹은 real measureable function)들의 집합을 $V$라고 하면, 이것은 (무한차원의) 벡터공간입니다. 이때, $E$는 $E:V\to\mathbb R$인 함수라고 생각할 수 있는데 이 $E$가 선형함수라는 뜻입니다. (더 구체적으로는, linear functional입니다.)

이 proposition으로부터 바로 얻을 수 있는 결과는

\[E[aX+b]=aE[X]+b\]

입니다. 또한

\[\begin{align*} {\sigma_X}^2 &=E[(X-\mu)^2]\\ &=E[X^2-2\mu X+\mu^2]\\ &=E[X^2]-2\mu E[X]+\mu^2\\ &=E[X^2]-2E[X]^2+E[X]^2\\ &=E[X^2]-E[X]^2 \end{align*}\]

도 얻을 수 있습니다. 이를 이용하여 Poisson distribution

\[P_K(k)=\frac{\lambda^k}{k!}e^{-\lambda}\]

의 분산을 구해보면

\[\begin{align*} E[K^2] &=\sum_{k=0}^\infty k^2P_K(k)\\ &=\sum_{k=0}^\infty k^2\frac{\lambda^k}{k!}e^{-\lambda}\\ &=\sum_{k=0}^\infty k(k-1)\frac{\lambda^k}{k!}e^{-\lambda} +\sum_{k=0}^\infty k\frac{\lambda^k}{k!}e^{-\lambda}\\ &=\sum_{k=2}^\infty k(k-1)\frac{\lambda^k}{k!}e^{-\lambda}+E[X]\\ &=\lambda^2\sum_{k=2}^\infty\frac{\lambda^{k-2}}{(k-2)!}e^{-\lambda}+E[X]\\ &=\lambda^2\sum_{m=0}^\infty\frac{\lambda^m}{m!}e^{-\lambda}+E[X]\\ &=\lambda^2+\lambda \end{align*}\]

으로부터

\[{\sigma_K}^2=E[K^2]-E[K]^2=(\lambda^2+\lambda)-\lambda^2=\lambda\]

입니다. 또한, exponential distribution

\[\begin{align*} f_X(x)= \begin{cases} \lambda e^{-\lambda x} &x\ge0\\ 0 &x\lt0 \end{cases} \end{align*}\]

의 분산을 구해보면

\[\begin{align*} E[X^2] &=\int_0^\infty x^2P_X(x)\,dx\\ &=\int_0^\infty x^2\lambda e^{-\lambda x}\,dx\\ &=\left[-x^2e^{-\lambda x}\right]_0^\infty+\int_0^\infty2xe^{-\lambda x}\,dx\\ &=0+\frac2\lambda\int_0^\infty x\lambda e^{-\lambda x}\,dx\\ &=\frac2\lambda\cdot E[X]=\frac2{\lambda^2} \end{align*}\]

이고

\[{\sigma_X}^2=E[X^2]-E[X]^2=\frac1{\lambda^2}\]

입니다.

06 조건부 평균

ex 3.13 geometric distribution

시행의 결과가 성공/실패의 두 종류로 나오는 시행을 Bernoulli trial이라고 합니다.

어떤 Bernoulli trial을 반복적으로 시행할 때, $K$번째에 처음으로 성공할 경우

에 $K$는

\[P_K(k)=(1-p)^{k-1}p\qquad(k=1,2,\cdots)\]

와 같은 PMF를 가집니다. 위 식에 대한 증명은 당연하기 때문에 생략하겠습니다. 이때, 이산확률변수 $K$가 geometric distribution을 따른다고 합니다.

예를 들어, 다음(칠판에 적힌 문장)과 같이 정의된 $K$는 geometric distribution을 따릅니다.

Let $K$ be the number of trials until the first success. For example, we may toss a die repeatedly until the first $6$.

그러니까, 주사위 하나를 반복적으로 던질 때, 주사위의 눈이 처음으로 6이 나오기까지의 시행횟수를 $K$라고 하면 $K$는 geometric distribution을 따릅니다.

$P_K(k)$가 PMF가 되기 위한 첫번째 조건인 $P_K(k)\ge0$를 만족시키는 것은 당연합니다. 두번째 조건도 (예의상) 확인해보면

\[\sum_{k=1}^\infty P_K(k)=p+p(1-p)+p(1-p)^2+\cdots=\frac p{1-(1-p)}=1\]

입니다. 다음으로 평균을 구해보면

\[\begin{align*} E[K] &=\sum_{k=1}^\infty kP_K(k)\\ &=\sum_{k=1}^\infty k(1-p)^{k-1}p\\ &=p+2(1-p)p+3(1-p)^2+\cdots\\ (1-p)E[K]&=(1-p)p+2(1-p)^2p+3(1-p)^3p \end{align*}\]

두 식을 적당히 빼면

\[pE[K]=p+(1-p)p+(1-p)^2p+\cdots=1\]

이고 $E[K]=\frac1p$입니다.

(강의에서는 미분을 통해 구한 것 같습니다만, 위와 같이 멱급수의 공비를 곱하는 방식으로 구해봤습니다. 하지만 지금 구한 방법으로는 분산을 구하기가 힘들 것 같으니, 미분의 방법으로 처음부터 다시 풀어보면)

다시 평균을 구하기 위해 평균 식

\[E[K]=\sum_{k=1}^\infty k(1-p)^{k-1}p\]

을 보면 $\sum_k (1-p)^k$와 같은 함수형태를 미분하는 것이 요긴할 것으로 보입니다. 등비급수의 식에 의해

\[\sum_{k=1}^\infty(1-p)^k=\frac{1-p}{1-(1-p)}=\frac{1-p}p=\frac1p-1\]

이고, 양변을 $p$에 대하여 미분한 뒤 마이너스를 붙이면

\[\begin{equation}\tag{$*$} \sum_{k=1}^\infty k(1-p)^{k-1}=\frac1{p^2} \end{equation}\]

입니다. 따라서

\[E[K]=\frac1{p^2}\times p = \frac1p\]

입니다. $E[K^2]$의 식도 보면

\[E[K^2]=\sum_{k=1}^\infty k^2(1-p)^{k-1}p\]

인데, 이것은 식 ($\ast$)을 미분하면 비슷한 식을 얻을 수 있습니다. ($\ast$)을 미분한 뒤 마이너스를 붙이면

\[\sum_{k=1}^\infty k(k-1)(1-p)^{k-2}=\frac2{p^3}\]

이고, 따라서

\[\begin{aligned} \sum_{k=1}^\infty k^2(1-p)^{k-2} &=\frac2{p^3}+\sum_{k=1}^\infty k(1-p)^{k-2}\\ &\stackrel{(\ast)}=\frac2{p^3}+\frac1{p^2(1-p)}\\ &=\frac{2(1-p)+p}{p^3(1-p)}\\ &=\frac{2-p}{p^3(1-p)} \end{aligned}\tag{$\ast\ast$}\]

이고,

\[E[K^2]=\sum_{k=1}^\infty k^2(1-p)^{k-1}p =\frac{2-p}{p^3(1-p)}\times p(1-p)=\frac{2-p}{p^2}\]

입니다. 따라서

\[{\sigma_K}^2=E[K^2]-E[K]^2=\frac{2-p}{p^2}-\frac1{p^2}=\frac{1-p}{p^2}\]

입니다.

이산확률변수 $K$가 $$P_K(k)=(1-p)^{k-1}p\qquad(k=1,2,\cdots)$$ 를 그 질량함수로 가질 때 $$X\sim\text{Geo}(p)$$ 로 표현하기도 합니다.

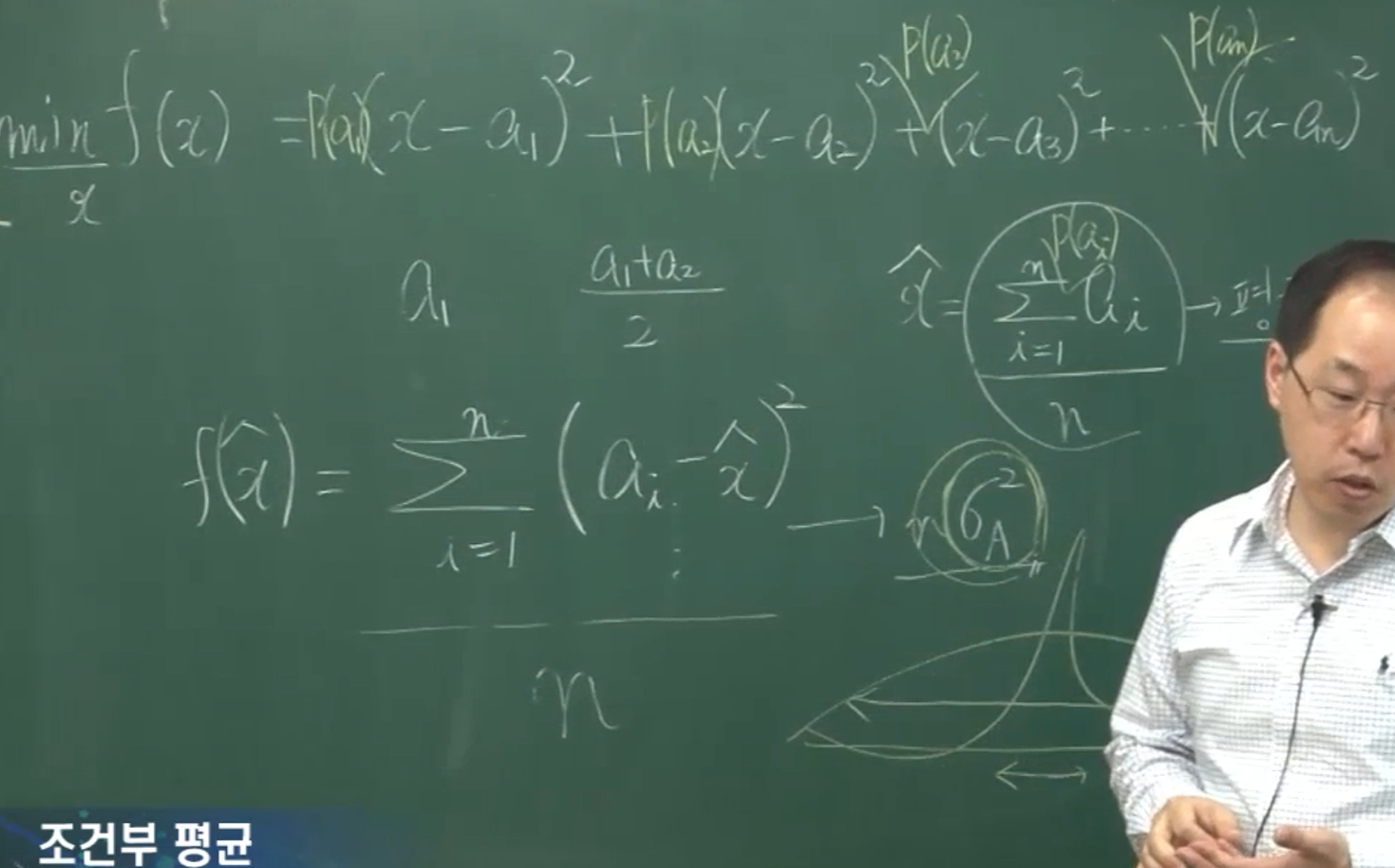
이후에는 평균과 분산의 의미에 대한 설명이 있습니다(위 캡쳐). computer vision에서의 얼굴인식문제를 아주 naive하게 생각할 때, 우리는 실제 카메라에 인식된 얼굴모양(실제값)이 우리가 정한 특정한 형태의 얼굴모양 (표준참값, 예측값, 추정값, 표준모델의 값)과 얼마나 비슷한지를 판단할만한 판단근거가 필요합니다.

이때의 실제값과 표준참값은 각각 벡터로 생각할 수 있고, 따라서 표준적인 벡터사이의 거리(의 제곱)인 $L^2$ norm(의 제곱)을 생각하게 됩니다. 그것은 실제값과 표준참값을 뺀 다음 제곱하여 성분별로 더하는 것을 말합니다. 그리고 이 값(통상 energy라고 부르기도 하는 값)이 최소가 되도록 하는 표준참값을, ‘괜찮은 모델’이라고 둘 수 있을 것입니다.

그런데 $L^2$ norm의 제곱, 즉 sum of squared errors(SSE)는 그 특성상 표준참값이 실제값들의 평균일 때에 최소가 되는 경향이 있습니다. (사실 표준참값-실제값 예는 multivariate이고 뒤에 나오는 예시는 univariate이라서 적절한 설명인지 잘 이해가 안가긴 하지만) 그리고 이것은 아까 간단하게 언급한 적이 있습니다. 즉

\[g(t)=\sum_{k=1}^n(t-x_k)^2\]

는 $t=\frac1n\sum_{k=1}^nx_k$일 때, 즉 $t$가 $x_k$들의 평균일 때 최소가 되는 것입니다. 즉

\[\text{arg}\min_t\sum_{k=1}^n(t-x_k)^2=\frac1n\sum_{k=1}^nx_k\]

이고

\[\min_t\sum_{k=1}^n(t-x_k)^2={\sigma_X}^2\]

인 것입니다. 증명은, 중학교 식으로 $ax^2+bx+c$의 최솟값을 구하는 식으로 해도 되고, 고등학교 식으로 미분을 사용해도 됩니다. 여기에서는 discrete uniform distribution인 경우에 대해서만 이야기한 셈이지만 일반적인 discrete distribution에 대해서도, 그리고 연속확률분포에 관해서도 마찬가지의 사실을 쉽게 증명할 수 있습니다.

반면

\[h(t)=\sum_{k=1}^n|t-x_k|\]

와 같은 값을 objective function으로 둘 수도 있을 것입니다. 이 경우에는 $t$가 $x_k$들의 중간값(median)일 때 $g(t)$가 최소임이 알려져있습니다. 이것은 그래프를 살짝 그려보기만 해도 알 수 있습니다. (아래 그림) 다만, 이 경우도 역시 discrete uniform distribution에 대한 논증인데, 일반적인 discrete distribution와 연속확률분포에 대해서는 다른 방식의 증명이 필요할 것입니다.

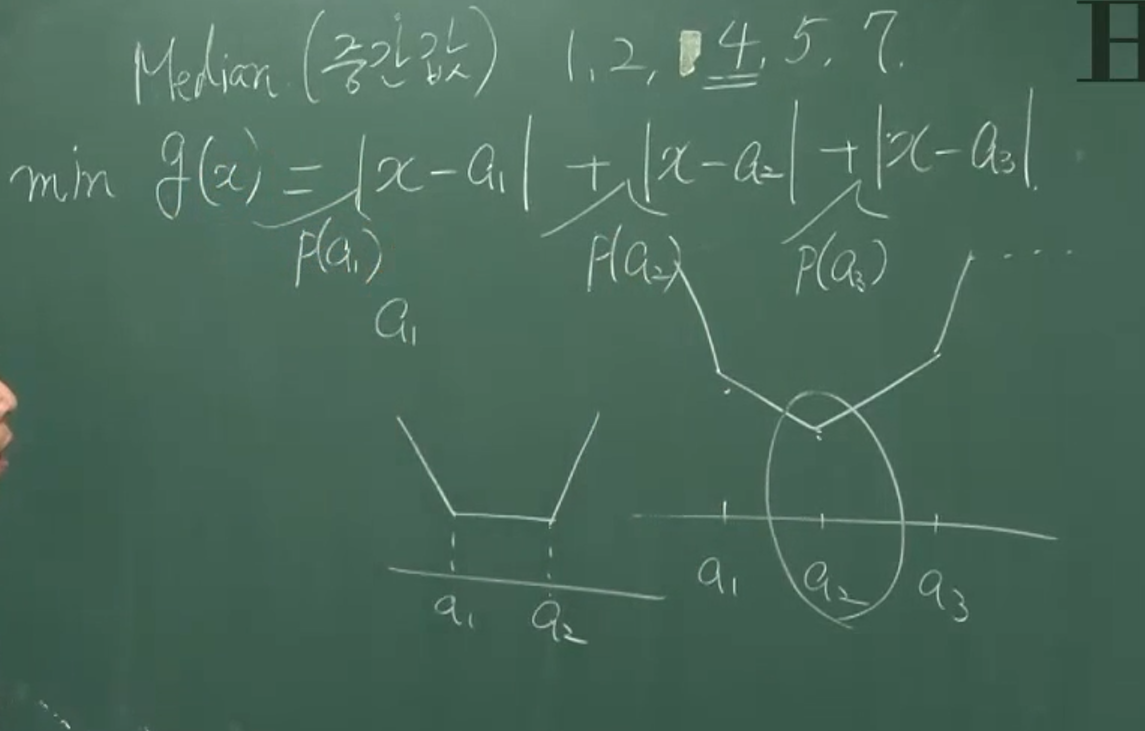
3.5 conditional expectation

이산확률변수의 conditional expectation(조건부기댓값)을 정의하기 전에, 먼저 conditional PMF(조건부 확률질량함수)를 다음과 같이 정의합니다.

\[P_X(x|A)=P(X=x|A)\]

그러면, 이산확률변수에서의 conditional expectation을

\[E[X|A]=\sum_{x_i\in A}x_iP_X(x_i|A)\]

로 정의할 수 있습니다. 여기에서 $A$는 사건(event, $A\subset S$)이라기보다는 실수들의 집합($A\subset\mathbb R$)인 것 같습니다. 그리고, $X=x_i$라는 표현이 마치 사건처럼 쓰여져있습니다. 따라서 $P_X(x_i|A)$는

\[P(\{w\in S:X(w)=x_i\}|\{w\in S:X(w)\in A\})\]

의 의미입니다.

이번에는 연속확률변수의 조건부 기댓값을 정의하겠습니다. 먼저 conditional CDF는

\[F_X(x|A)=P(X\le x|A)\]

로 정의됩니다. conditional PDF는 PDF의 정의에서와 마찬가지로 미분을 통해 얻을 수 있습니다.

\[\begin{align*} f_X(x|A) &=\lim_{\Delta x\to0+}\frac{P\left(x<X\le x+\Delta x|A\right)}{\Delta x}\\ &=\lim_{\Delta x\to0+}\frac{F_X(x+\Delta x|A)-F_X(x|A)}{\Delta x}\\ &=\frac d{dx}F_X(x|A) \end{align*}\]

입니다. 이를 통해 conditional expectation을

\[E[X|A]=\int_{x\in A}xf_X(x|A)\,dx\]

로 정의할 수 있습니다.

ex. 3.14

사건 $A=\{X\le a\}$에 대하여 conditional CDF와 conditional PDF를 구해봅니다. 이때 $A$는

\[A=\{w\in S:X(w)\le a\}\]

라는 의미입니다. 이때 $X$의 CDF와 PDF는 이미 주어져 있다고 가정합니다. 그러니까, $F_X(x)$와 $f_X(x)$를 사용하여 $F_X(x|A)$와 $f_X(x|A)$를 구하는 것이 목적입니다. conditional CDF $F_X(x|A)$ 를 먼저 계산하면

\[\begin{align*} F_X(x|A) &=P\left(X\le x|X\le a\right)\\ &=\frac{P\left(X\le x\cap X\le a\right)}{P(x\le a)} \end{align*}\]

입니다. 두 경우가 있을 수 있는데, 만약 $x\gt a$이면,

\[F_X(x|A)=\frac{P(X\le a)}{P(X\le a)}=1\]

이 됩니다. 만약 $x\le a$이면

\[F_X(x|A)=\frac{P(X\le x)}{P(X\le a)}=\frac{F_X(x)}{F_X(a)}\]

가 됩니다. 정리하면

\[F_X(x|A)= \begin{cases} 1&(x\gt a)\\ \frac{F_X(x)}{F_X(a)}&(x\le a) \end{cases}\]

입니다. 다음으로, condtional PDF $f_X(x|A)$를 구하면

\[f_X(x|A) =\frac d{dx}F_X(x|A) =\begin{cases} 0&(x\gt a)\\ \frac{f_X(x)}{F_X(a)}&(x\le a) \end{cases}\]

입니다.

ex. 3.15

이번에는 PDF가

\[f_X(x)=\frac1{20},\quad 40\le x\le 60\]

로 주어지고, 사건 $A$가

\[A=\{X\le 55\}\]

인 경우를 보겠습니다. conditionoal CDF는

\[F_X(x|A)=P(X\le x|X\le 55) =\frac{P\left((X\le x)\cap(X\le55)\right)}{P(X\le55)} =\begin{cases} 0 &(x\lt40)\\ \frac{x-40}{15} &(40\le x\lt55)\\ 1 &(x\ge55) \end{cases}\]

이고 conditionoal PDF는

\[f_X(x|A)=\frac d{dx}F_X(x|A) =\begin{cases} \frac1{15} &(40\lt x\lt55)\\ 0 &(\text{otherwise}) \end{cases}\]

입니다. 또한, condtional expectation은

\[\begin{align*} E[X|A] &=\int_{x\in A}xf_X(x|A)\,dx\\ &=\int_{40}^{55}\frac1{15}x\,dx\\ &=\frac1{15}\frac12(55-40)(55+40)\\ &=\frac{95}2\\ &=47.5 \end{align*}\]

입니다. 그냥 의미적으로 해석해보면, 원래 $X$는 40과 60 사이에 균일하게 분포되어 있었는데, 여기에 $X$가 55보다 작다는 조건 $A$를 준 것입니다. 그러면 이 조건 하에서 $X$는 40과 55 사이에 균일하게 분포되어 있습니다. 따라서 이 조건 하에서의 평균은 $\frac{40+55}2=47.5$가 되어야 합니다.

그런 것 치고는 위의 계산은 불필요하게 복잡한 것 같습니다. 저 위의 계산처럼 conditional density를 사용하지 않는 방법은 크게 없을 것 같습니다. conditional PDF로 바로 변환되는 것이 아니기 때문입니다. 굳이 다른 방법을 찾자면 부분적분을 사용해 conditional CDF를 사용할 수도 있을 것 같습니다.

07 여러가지 이산확률분포

3.6 Chebysev inequality

체비셰프의 부등식. 이름은 들어봤지만, 제대로 보는 것이 처음이라는 게 상당히 유감스럽습니다. 학부때 확률론을 계속해서 피해다녔더니, 이제서야 보게 되었습니다.

그런데, 아주 재미있는 부등식인 것 같습니다. 확률변수 $X$와 양의 실수 $a$에 대하여 아래의 부등식이 성립합니다. 이것을 Chebysev inequality라고 부릅니다.

\[P\left(\big|X-E[X]\big|\ge a\right)\le\frac{\,{\sigma_X}^2}{a^2}\]

$X$가 평균으로부터 어느 정도의 간격($a$) 이상 떨어져있을 확률은 그 간격에 의존하는 어떤 값$\left(\frac{\,{\sigma_X}^2}{a^2}\right)$보다 작다는 뜻입니다.

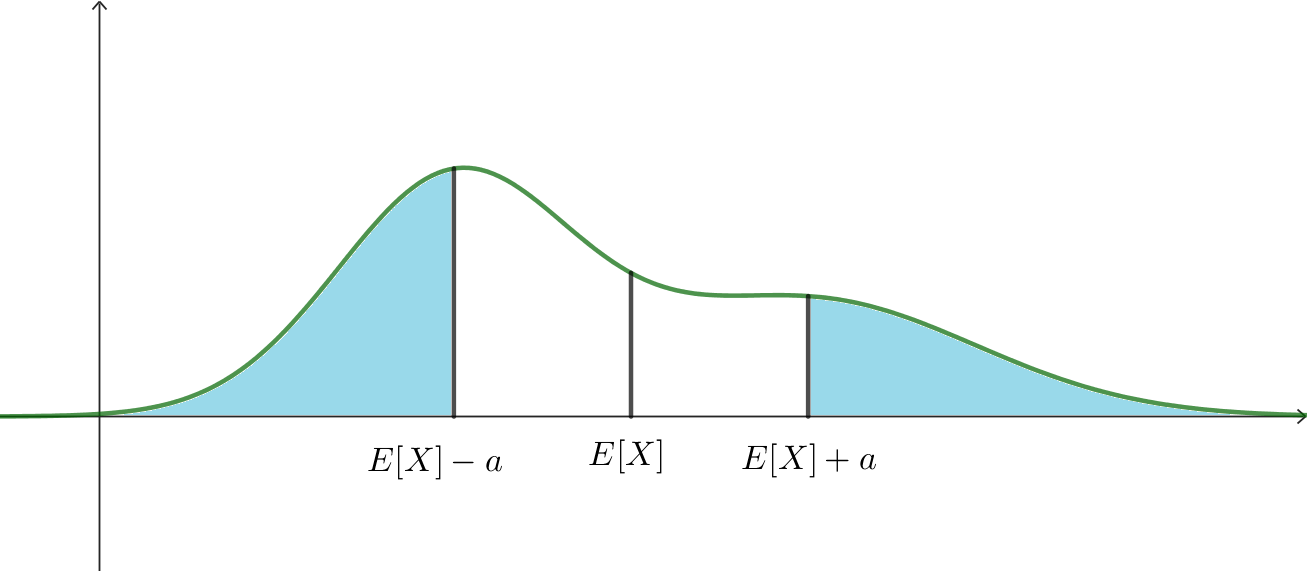
예를 들어 $a=2\sigma_X$인 경우에 있어서의 Chebysev inequality는 $X$가 2-sigma 바깥에 있을 확률이 $\frac14$보다 작다는 것을 의미합니다;

\[P\left(\big|X-E[X]\big|\ge 2\sigma_X\right)\le\frac14\]

만약 정규분포의 상황을 가정하면, 아래 그림에서 하늘색으로 표시된 부분의 면적이 $\frac14$보다 작다는 것입니다.

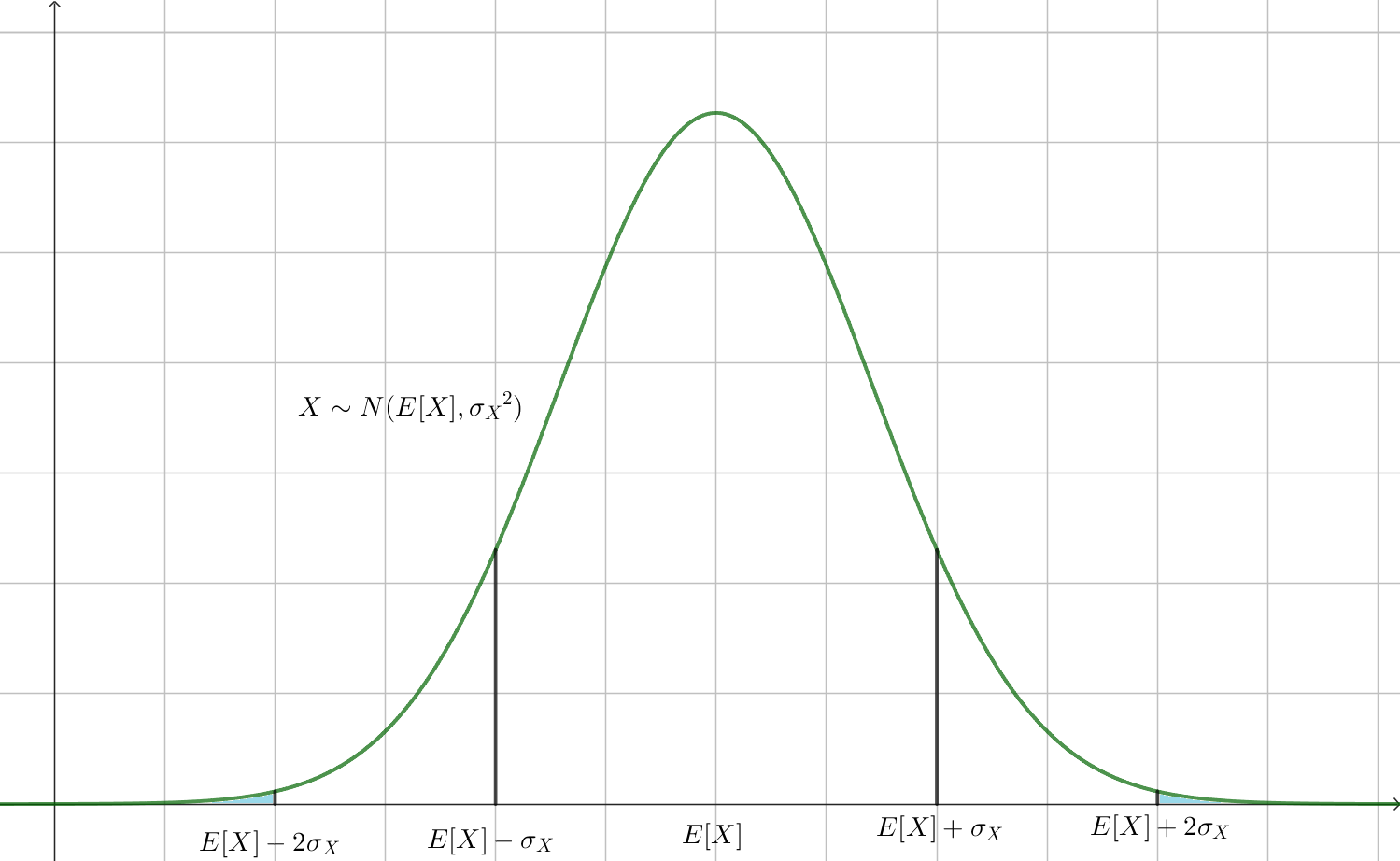
이 부등식이 아주 tight한 것 같지는 않습니다. 만약, $X$가 정규분포를 따른다면, $a=2\sigma_X$에 대한 확률은

\[\begin{align*} P\left(|X-E[X]|\ge2\sigma_X\right) &=P\left(|Z|\ge2\right)\\ &=2\left(1-P\left(0\le Z\le2\right)\right)\\ &=2(0.5-0.47725)\\ &=0.0455 \end{align*}\]

입니다(표준정규분포표의 값을 활용했습니다.) 그러니까, Chebysev inequailty를 통해 얻는 확률의 upper bound는 0.25였는데, 실제 확률의 값은 0.0455입니다. 따라서 이 경우는 Chebysev inequality의 결과를 (당연히) 만족시키기는 합니다. 그런데 그 결과라는 게 실제값보다 꽤 큽니다. 그런 의미에서 Chebysev inequality는 모든 종류의 확률변수에 대하여 일반적인 upper bound를 제시하는 것이라고 이해해야 할 것 같습니다.

연속확률변수에 대한 Chebysev inequality는, ${\sigma_X}^2$을 들여다보면 쉽게 증명됩니다.

\[\begin{align*} {\sigma_X}^2 &=\int_{-\infty}^\infty\left(x-E[X]\right)^2f_X(x)\,dx\\ &=\int_{|x-E[X]|\ge a}\left(x-E[X]\right)^2f_X(x)\,dx +\int_{|x-E[X]|\lt a}\left(x-E[X]\right)^2f_X(x)\,dx\\ &\ge a^2\int_{|x-E[X]|\ge a}f_X(x)\,dx\\ &=a^2P\left(|x-E[X]|\ge a\right) \end{align*}\\\]

강의에서, 이산확률변수에 대한 증명은 조금 tricky할 수 있다고 했는데, 그래도 한 번 해보면

\[\begin{align*} {\sigma_X}^2 &=\sum_{i=1}^n\left(x_i-E[X]\right)^2P_X(x_i)\\ &=\sum_{|x_i-E[X]|\ge a}\left(x_i-E[X]\right)^2P_X(x_i) +\sum_{|x_i-E[X]|\lt a}\left(x_i-E[X]\right)^2P_X(x_i)\\ &\ge a^2\sum_{|x_i-E[X]|\ge a}P_X(x_i)\\ &=a^2P\left(|x-E[X]|\ge a\right) \end{align*}\\\]

입니다. (되는데?) “expectation 값이 random variable이 아닐 수도 있다”는 말씀이 무슨 의미인지 잘 모르겠습니다. 이 사람은 제가 한 것과 똑같은 증명을 적어놓았고, wikipedia에는 conditional expectation의 성질을 사용하여 (그러니까 summation이나 integral을 사용하지 않고) 증명했습니다.

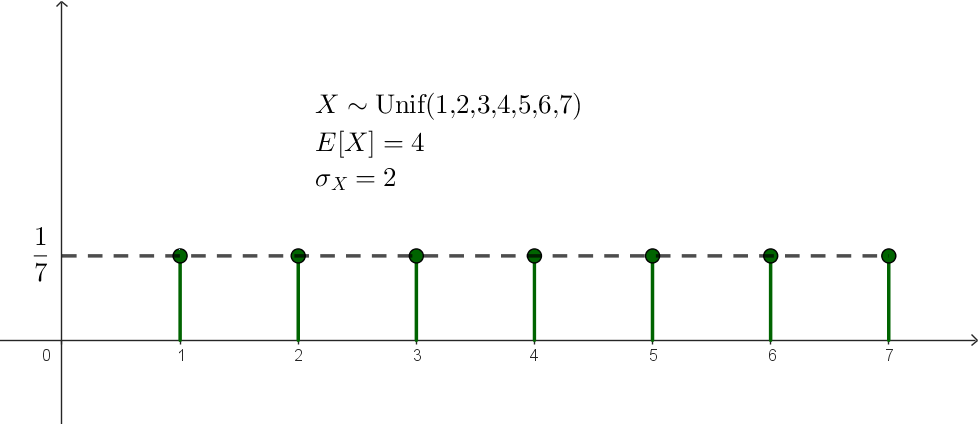
이번에는 discrete uniform한 경우의 예를 살펴봤습니다. $X$가 집합 $\{1,2,3,4,5,6,7\}$의 uniform distribution을 따를 때, $X$의 평균은

\[E[X]=4\]

이고, 표준편차는

\[\sigma_X=\sqrt{\frac17\left(9+4+1+0+1+4+9\right)}=2\]

입니다. Chebysev inequality의 식

\[P\left(\big|X-E[X]\big|\ge a\right)\le\frac{\,{\sigma_X}^2}{a^2}\]

에서 $a=2.5$를 대입하면

\[\frac27\le\frac{2^2}{2.5^2}\]

가 되어, Chebysev inequality가 여전히 성립합니다.

Chapter 4. Special Distributions

'Bernoulli'는 '베르누이'라고 보통 쓰기도 하지만, 원래 발음은 베르눌리 라고 읽는 것이 맞는 것 같습니다. 마찬가지로 Poisson은 푸아상 으로 발음하는 것이 맞는 것 같습니다.

4.2 Bernoulli distribution

앞서, Bernoulli trial(베르눌리 시행)이 근원사건의 개수가 $2$개인 시행을 말한다고 했습니다. 즉, $|S|=2$인 경우

\[S=\{w_1,w_2\}\]

를 말합니다. 많은 경우에 $w_1$을 ‘성공’으로, $w_2$를 ‘실패’로 해석했었습니다.

다음은 위키피디아의 정의입니다.

A Bernoulli trial (or binomial trial) is a random experiment with exactly two possible outcomes, “success” and “failure”, in which the probability of success is the same every time the experiment is conducted.

예를 들어

\[\begin{cases} X(w_1)=-2\\ X(w_2)=3 \end{cases}\]

로 정의하면 이것은 Bernoulli distribution에 해당할 것 같습니다. 하지만, 통상

\[\begin{cases} X(w_1)=1\\ X(w_2)=0 \end{cases}\]

인 경우를 가정합니다.

$P_X(X=1)=p$라고 하면 $P_X(X=0)=1-p$이고, 따라서 Bernoulli distribution은 오로지 하나의 값 $p$에 의해 결정되는 분포입니다. 기록을 위해 PMF를 적어보면

\[P_X(x)= \begin{cases} p &(x=1)\\ 1-p &(x=0) \end{cases} \tag{$\ast$}\]

입니다.

예를 들어, 동전을 하나 던졌을 때 앞면이 나오면 $X=1$로 정하고 뒷면이 나오면 $X=0$으로 정하면, 이 시행은 Bernoulli trial이고 ; $S=\{H,T\}$, $|S|=2$, $X$의 분포는 Bernoulli distribution입니다. 그리고 $X$는

\[\begin{cases} X(H)=1\\ X(T)=0 \end{cases}\]

와 같이 주어집니다.

$(\ast)$는 다음과 같이 한 줄의 식으로 쓸 수도 있습니다. (조금 쓸데없어보이기도 하고, 그냥 현학적인 표현인 것처럼 보이기도 하지만, 많은 경우에 Bernoulli distribution이 이와 같이 표현되니 알아두어도 나쁘지는 않을 것 같습니다.) 덧셈의 형태로

\[P_X(x)=(1-p)(1-x)+px,\qquad x\in\{0,1\}\]

와 같이 쓸 수도 있고, 아니면 곱셈의 형태로

\[P_X(x)=p^x(1-p)^{1-x},\qquad x\in\{0,1\}\]

와 같이 쓸 수도 있습니다.

Beroulli distribution는 가장 간단한 형태의 분포입니다. Bernoulli distribution보다 더 간단한 형태는 $|S|=1$인 경우겠지만, 그 경우는 확률적으로 이야기하는 것 자체가 의미가 없습니다. Bernoulli distribution의 평균과 분산은 아주 쉽게 계산됩니다.

\[\begin{align*} E[X] &=0\times P_X(0)+1\times P_X(1)\\ &=0\times(1-p)+1\times p\\ &=p\\ {\sigma_X}^2 &=(0-E[X])^2\times P_X(0)+(1-E[X])^2\times P_X(1)\\ &=(0-p)^2\times(1-p)+(1-p)^2\times p\\ &=p(1-p)\left(p+(1-p)\right)\\ &=p(1-p) \end{align*}\]

4.3 binomial distribution

어떤 Bernoulli trial을 $n$번 반복적으로 시행할 때 성공의 횟수

를 $X$라고 할 때, $X$는

\[P_X(x)=\binom nxp^x(1-p)^{n-x}\qquad(x=0,1,\cdots,n)\]

를 PMF로 가집니다. 이때, $X$가 이항분포를 따른다고 합니다.

위의 PMF 식의 증명은 당연하므로 생략하겠습니다. 위의 함수 $P_X$는 $x=0$, $\cdots$, $x=n$일 때에 대하여 모두 더했을 때 1이 됩니다;

\[\begin{align*} \sum_{x=0}^nP_X(x) &= \sum_{x=0}^n\binom nxp^x(1-p)^{n-x}\\ &=\left(p+(1-p)\right)^n\\ &=1 \end{align*}\]

이항분포의 평균과 분산이 각각 $np$, $np(1-p)$이라는 것은 $\langle02\rangle$-(1.10.4)에서 이미 증명했습니다. 그 때에는 $(1+x)^n$을 미분하여 얻을 수 있는 성질로부터 증명했었습니다. 강의에서는 표준적인 방법 (combination의 성질)으로 증명하고 있습니다.

\[\begin{align*} E[X] &=\sum_{x=0}^nxP_X(x)\\ &=\sum_{x=0}^nx\binom nxp^x(1-p)^{n-x}\\ &=\sum_{x=1}^nx\binom nxp^x(1-p)^{n-x}\\ &\stackrel\star=\sum_{x=1}^nn\binom{n-1}{x-1}p^x(1-p)^{n-x}\\ &=np\sum_{x=1}^n\binom{n-1}{x-1}p^{x-1}(1-p)^{(n-1)-(x-1)}\\ &=np\sum_{y=0}^{n-1}\binom{n-1}yp^y(1-p)^{(n-1)-y}\\ &=np\left(p+(p-1)\right)^{n-1}\\ &=np\\ E[X^2] &=\sum_{x=0}^nx^2P_X(x)\\ &=\sum_{x=0}^nx^2\binom nxp^x(1-p)^{n-x}\\ &=\sum_{x=0}^n(x^2-x)\binom nxp^x(1-p)^{n-x}+\sum_{x=0}^nx\binom nxp^x(1-p)^{n-x}\\ &=\sum_{x=2}^nx(x-1)\binom nxp^x(1-p)^{n-x}+np\\ &\stackrel{\star\star}=\sum_{x=2}^nn(n-1)\binom{n-2}{x-2}p^x(1-p)^{n-x}+np\\ &=n(n-1)p^2\sum_{x=2}^n\binom{n-2}{x-2}p^{x-2}(1-p)^{(n-2)-(x-2)}+np\\ &=n(n-1)p^2\sum_{y=0}^{n-2}\binom{n-2}yp^y(1-p)^{(n-2)-y}+np\\ &=n(n-1)p^2\left(p+(1-p)\right)^{n-2}+np\\ &=n(n-1)p^2+np\\ &=n^2p^2-np^2+np\\ V[X] &=E[X^2]-E[X^2]\\ &=n^2p^2-np^2+np-(np)^2\\ &=np-np^2\\ &=np(1-p) \end{align*}\]

위의 계산들 중 $\star$와 $\star\star$는 combination의 성질을 사용한 것입니다. $\star$만 증명하면

\[\begin{align*} x\binom nx &=x\times\frac{n!}{x!(n-x)!}\\ &=n\times\frac{(n-1)!}{(x-1)!((n-1)-(x-1))!}\\ &=n\binom{n-1}{x-1} \end{align*}\]

입니다. $\star\star$도 마찬가지의 방법으로 하면 쉽게 증명될 수 있습니다.

강의에서는, 이 증명방법보다 더 간결한 증명방식도 소개합니다. 함수 $f$를

\[f(t)=\left(pt+(1-p)\right)^n=\sum_{x=0}^n\binom nxp^xt^x(1-p)^{n-x}\]

와 같이 정의하고, $f’(1)$와 $f’‘(1)$을 각각 계산해보면

\[\begin{align*} f'(t)&=np\left(pt+(1-p)\right)^{n-1}&&=\sum_{x=0}^nx\binom nxp^xt^{x-1}(1-p)^{n-x}\\ f'(1)&=np\left(p+(1-p)\right)^{n-1}&&=\sum_{x=0}^nx\binom nxp^x(1-p)^{n-x}\\ &=np&&=E[X]\\ f''(t)&=n(n-1)p^2\left(pt+(1-p)\right)^{n-2}&&=\sum_{x=0}^nx(x-1)\binom nxp^xt^{x-2}(1-p)^{n-x}\\ f''(1)&=np\left(p+(1-p)\right)^{n-1}&&=\sum_{x=0}^nx(x-1)\binom nxp^x(1-p)^{n-x}\\ &=n(n-1)p^2&&=E[X^2]-E[X]\\ \end{align*}\]

이 됩니다. 마지막 식을 정리하면

\[E[X^2]=n^2p^2-np^2+np\]

가 되고, 이것으로 ${\sigma_X}^2$을 구하면

\[\begin{align*} {\sigma_X}^2 &=E[X^2]-E[X]^2\\ &=(n^2p^2-np^2+np)-n^2p^2\\ &=-np^2+np\\ &=np(1-p) \end{align*}\]

입니다. 이와 같이 binomal distribution의 평균과 표준편차를 구할 수 있습니다.

4.4 geometric distribution

geometric distribution을 따르는 확률변수 $K$가 PMF와 평균, 분산을

\[\begin{align*} P_K(k)&=(1-p)^{k-1}p\quad(k=1,2,\cdots)\\ E[K]&=\frac1p\\ {\sigma_X}^2&=\frac{1-p}{p^2} \end{align*}\]

와 같이 가진다는 것을 확인한 바 있습니다. 여기에서 $K$의 의미는

the number of Bernoulli trial until the first success

입니다. 다시 말해($\langle06\rangle$의 3.13에서 소개한 표현을 다시 쓰면),

어떤 Bernoulli trial을 반복적으로 시행할 때, $K$번째에 처음으로 성공할 경우

의 $K$값을 말합니다. 그러니까, 어떤 Bernoulli trial을 연속해서 시행할 때, 처음 $k-1$번은 실패하고 $k$번째에 성공할 경우에 확률변수 $K$를 $K=k$로 지정하면 $K$가 geometric distribution을 따른다고 합니다.

memorylessness(forgetfulness)

memoryless property란 여러 번의 Bernoulli trial에서 앞서의 결과가 이후의 결과에 영향을 미치지 않는다는 성질을 뜻합니다. 그리고, geometric distribution은 memoryless property를 가지고 있습니다.

geometric distribution을 따르는 확률변수 $X$에 대하여 $k$번째에 성공할 확률, 그러니까, $1$번째, $2$번째, $\cdots$, $k-1$번째까지는 실패했지만, $k$번째에는 성공할 확률은 $P(X=k)$입니다. geometric distribution이 memoryless property를 가진다는 것은 이 Bernoulli trial을 여러 번 시행했다고 하더라도, 이후 $k$번째에 성공할 확률이 여전히 $P(X=k)$라는 것입니다. 그러니까, $n$번의 시행 이후 $n+1$번째, $n+2$번째, $\cdots$, $n+k-1$번째까지는 실패했지만 $n+k$번째에는 성공할 확률이 $P(X=k)$와 같아야 합니다.

문제를 간단하게 하기 위해, 앞의 $n$번째의 시행이 모두 실패했다고 가정하겠습니다. 이 가정은 $X>n$이라는 식으로 표현될 수 있습니다. 그러면 구해야 하는 확률은, $1$번째, $2$번째, $\cdots$, $n$번째, $\cdots$, $n+k-1$번째까지는 실패했지만, $n+k$번째에는 성공할 확률을 구해야 합니다. 이것은 $X=n+k$라는 식으로 표현될 수 있습니다.

따라서, $n$번째까지의 시행이 모두 실패했다고 가정했을 때, 그 이후 $k$번째에 성공할 확률은 $P(X=n+k|X>n)$으로 표현될 수 있습니다. 이것이 $P(X=k)$와 같은지를 확인해보려고 합니다. 실제로 계산해보면

\[\begin{align*} P\left(X=n+k|X>n\right) &=\frac{P\left((X=n+k)\cap(X>n)\right)}{P(X>n)}\\[10pt] &=\frac{P\left(X=n+k\right)}{P(X>n)}\\[15pt] &=\frac{(1-p)^{n+k-1}p}{\sum_{x\ge n+1}(1-p)^{x-1}p}\\[15pt] &=\frac{(1-p)^{n+k-1}}{\sum_{x\ge n+1}(1-p)^{x-1}}\\[15pt] &=\frac{(1-p)^{n+k-1}}{\frac{(1-p)^n}{1-(1-p)}}\\[15pt] &=(1-p)^{k-1}p\\ &=P\left(X=k\right) \end{align*}\]

입니다. 따라서 geometric distribution에 대해서는 memoryless property가 성립합니다. 즉, 지금 하는 것은 독립시행이므로, 앞서의 결과가 이후의 시행에 영향을 미치지 않는 것이 당연한데, 그 사실을 다시 한 번 확인해본 것입니다.

08 지수분포와 어랑분포

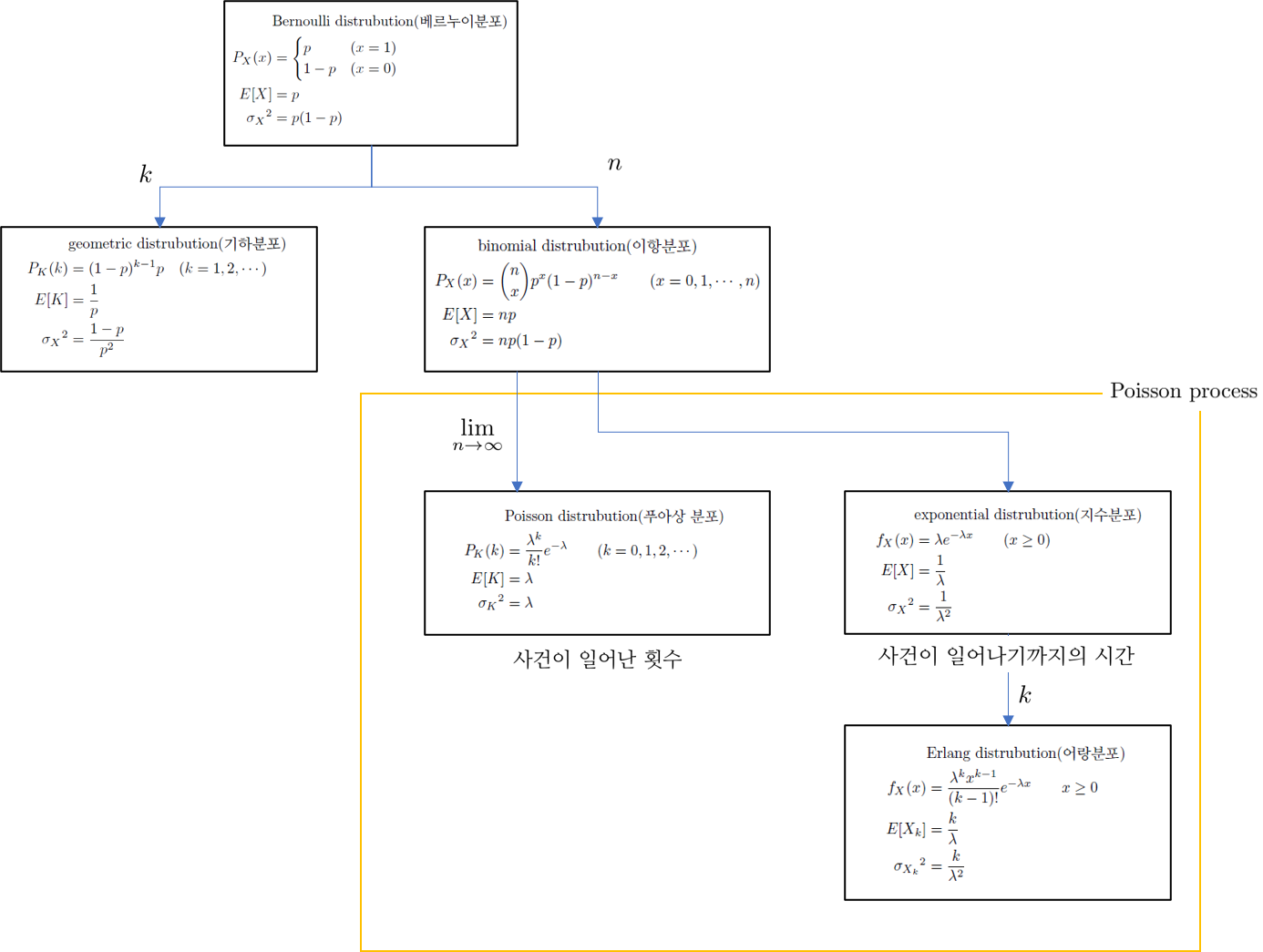
4.7 Poisson distribution

Poisson distribution을 따르는 확률변수 $K$가 PMF와 평균, 분산을

\[\begin{align*} P_K(k)&=\frac{\lambda^k}{k!}e^{-\lambda}\qquad(k=0,1,2,\cdots)\\ E[K]&=\lambda\\ {\sigma_K}^2&=\lambda \end{align*}\]

와 같이 가진다는 것을 확인한 바 있습니다. 여기에서 $K$의 의미는

the number of Bernoulli success in a time interval

였습니다. $\langle05\rangle$ 3.3에서 소개한 표현을 다시 쓰면

단위시간동안 평균적으로 $\lambda$번의 사건이 일어난다고 기대될 때, 단위시간동안 사건이 일어난 횟수

을 말합니다. 그런데, PMF의 식에서 ‘단위시간’이라는 것은 전제되어 있지 않습니다. 그리고 생각해보면, universal한 의미의 ‘단위시간’이라는 건 없습니다. 그래서 $K$의 의미를

$t$시간동안 평균적으로 $\lambda$번의 사건이 일어난다고 기대될 때, $t$시간동안 사건이 일어난 횟수

라고 정해도 상관 없습니다.

어떤 사건이 일어난다는 것은, 그 자체로 Bernoulli trial이라고 볼 수 있습니다. (사건이 일어난다 / 일어나지 않는다)와 같이 두 가능성 중 하나가 발생되는 것이기 때문입니다. 어떤 사건이 일정한 비율로 일어나는 경향을 보일 때, 특정한 시간 간격동안 어떤 사건이 일어난 횟수를 $K$라고 할 수 있는 것입니다.

(wikipedia)에는 다음과 같이 적혀있습니다.

The Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant mean rate and independently of the time since the last event.

For instance, a call center receives an average of 180 calls per hour, 24 hours a day. The calls are independent; receiving one does not change the probability of when the next one will arrive. The number of calls received during any minute has a Poisson probability distribution with mean 3: the most likely numbers are 2 and 3 but 1 and 4 are also likely and there is a small probability of it being as low as zero and a very small probability it could be 10.

Another example is the number of decay events that occur from a radioactive source during a defined observation period.

Poisson PMF의 식의 의미를 여러가지로 알아보다가 아주 재미있는 결과를 발견했습니다. 이 결과를 사용하면, Poisson PMF의 의미를 더 정확하게 알 수 있습니다. 그 내용은 이렇습니다. binomial PMF인

\[P_X(k)=\binom nkp^k(1-p)^{n-k}\]

에서 $n$을 무한대로 보내면, Poisson PMF의 모양이 됩니다.

\[\lim_{n\to\infty}\binom nkp^k(1-p)^{n-k}= \frac{\lambda^k}{k!}e^{-\lambda}\]

단, $\lambda$는 $p=\frac\lambda n$으로 주어집니다. 이에 대한 증명은 어렵지 않은데

\[\begin{align*} \lim_{n\to\infty}\binom nkp^k(1-p)^{n-k} =&\lim_{n\to\infty}\frac{n(n-1)(n-2)\cdots(n-k+1)}{k!}\left(\frac\lambda n\right)^k\left(1-\frac\lambda n\right)^{n-k}\\ =&\lim_{n\to\infty}\frac{n(n-1)(n-2)\cdots(n-k+1)}{n^k}\frac{\lambda^k}{k!}\left(1-\frac\lambda n\right)^{n-k}\\ =&\frac{\lambda^k}{k!} \lim_{n\to\infty}\frac{n-1}n \times\lim_{n\to\infty}\frac{n-2}n \times\cdots \times\lim_{n\to\infty}\frac{n-k+1}n \times\lim_{n\to\infty} \left(1-\frac\lambda n\right)^{n-k}\\ =&\frac{\lambda^k}{k!}\lim_{n\to\infty}\left(1-\frac\lambda n\right)^{n-k}\\ =&\frac{\lambda^k}{k!} \lim_{n\to\infty}\left(1-\frac\lambda n\right)^n \lim_{n\to\infty}\left(1-\frac\lambda n\right)^{-k}\\ =&\frac{\lambda^k}{k!} \lim_{n\to\infty}\left(\left(1-\frac\lambda n\right)^{-\frac n\lambda}\right)^{-\lambda}\times1\\ =&\frac{\lambda^k}{k!} \left(\lim_{n\to\infty}\left(1-\frac\lambda n\right)^{-\frac n\lambda}\right)^{-\lambda}\\ =&\frac{\lambda^k}{k!}e^{-\lambda} \end{align*}\]

이기 때문입니다.

Poisson PMF의 정확한 의미를 알기 위해서 DeGroot, Probability and Statistics, 4ed의 Example 5.4.1, 5.4.2를 읽어봤습니다. 설명이 잘 되어 있어서, 여기에 소개해보면 다음과 같습니다.

어떤 가게에 손님이 한 시간에 4.5명 꼴로 들어옵니다. 그럴 때에, 어느 날의 어느 시각으로부터 한 시간동안 들어온 손님의 수를 $X$라고 하면, $X$의 분포를 어떻게 이해하면 좋을지 생각해볼 수 있습니다.

그 답은 $\lambda=4.5$로 하는 Poisson distribution입니다.

위 문제를 풀기 위해 할 수 있는 자연스러운 방법은, 한 시간을 작은 시간단위로 쪼개는 것입니다. 예를 들어 1초 단위로 쪼개본다고 하겠습니다(1시간 = 3600초). 어느 날의 어느 시각으로부터 한 시간동안(예를 들어, 어느 날 오후 1시부터 오후 2시까지)의 시간을

• 1시 00분 00초 ~ 1시 00분 01초 : $T_1$
• 1시 00분 01초 ~ 1시 00분 02초 : $T_2$

$\qquad\vdots$

• 1시 59분 59초 ~ 2시 00분 00초 : $T_{3600}$

의 3600개 시간간격으로 나눌 수 있는 것입니다. 1시간에 4.5명 꼴로 손님이 들어온다고 했으니까, 1초에 $4.5/3600=0.00125$명 꼴로 손님이 들어옵니다. 그러니까 각각의 $T_i$ 동안 0.00125명 꼴로 손님이 들어옵니다. 그러면, $T_i$ 동안 손님이 들어오는 횟수는 거의 0입니다. 어쩌다가 한 명 들어오는 것이고 두 명 이상 들어올 가능성은 거의 없습니다. (실제로는 친구나 가족과 함께 방문할 수도 있으므로 현재로서는 이 가정이 좋은 가정은 아닐테지만, 어쨌든 수치상으로는 그렇습니다.) 그러니까 각각의 $T_i$에 대하여 손님이 들어오지 않거나(0명), 아니면 들어오거나(1명) 한다고 가정할 수 있습니다. 즉, 한 번의 시행은 그 결과값이 0 아니면 1인 Bernoulli trial이고 이때 $p=0.00125$입니다. 그런데 이런 시행이 한 번 있는 것이 아니라 3600번 있습니다. 각각의 시행들이 독립적이라고 가정하면, $X$는 $B(3600, 0.00125)$인 이항분포를 따릅니다. 따라서 한 시간동안 들어온 손님의 수가 $x$인 확률은

\[P(X=x)=\binom{3600}x(0.00125)^x(0.99875)^{3600-x}\tag{$\ast$}\]

입니다.

그런데 한 시간을 1초 단위로 자른 것은, 그냥 1초가 익숙해서 그렇게 한 것이지 어떤 특별한 의미가 있는 것은 아닙니다. 예를 들어 0.1초로 자를 수도 있습니다. 그 경우에는 총 36000개의 시간간격이 존재할 것이고 $X$는 $B(36000,0.000125)$를 따를 것이며

\[P(X=x)=\binom{36000}x(0.000125)^x(0.999875)^{36000-x}\tag{$\ast\ast$}\]

이 될 것입니다. 그리고 이 때에는 아까의 가정(하나의 시간간격동안 2명 이상 들어오지 않는다는 가정)이 더 그럴듯하게 성립할 것이므로 $(\ast\ast)$의 분포는 $(\ast)$의 분포보다 더 괜찮은 (현상을 잘 반영하는) 분포일 것입니다. 심지어는, 아무리 친구 두 명이서 함께 가게를 방문한다고 하더라도, 두 명의 사람이 가게에 들어오는 시각에는 미세하게 차이가 있을 것이므로 시간간격을 충분히 줄이면 이 가정은 항상 성립한다고 말할 수도 있을 것입니다. 그래서 3600, 36000이었던 값을 양의 무한대로 보내버리고, 아까의 계산결과를 적용하면

\[P(X=x) =\lim_{n\to\infty} \binom nx\left(\frac{4.5}n\right)^x\left(1-\frac{4.5}n\right)^{n-x} =\frac{4.5^x}{x!}e^{-4.5}\]

이 되는데 이것은 $\lambda=4.5$인 Poisson PMF입니다. $\square$

Poisson process
Poisson distribution에 대한 위의 설명은, 1시간동안 손님이 $4.5$명 들어오는 경향이 있다면, 30분동안에는 $2.25$명의 손님이 들어온다는 식의 가정에 근거하고 있습니다. 즉, $t$시간 동안에는 $4.5t$명의 손님이 들어온다고 가정하고 있습니다. 또한, 각각의 손님들이 들어오는 사건이 독립적이라는 가정도 깔려 있습니다. 즉, Poisson PMF의 의미가 설명되기 위해서는 위의 두 가정이 전제되어야 합니다. 위의 두 가정이 성립하는 상황을 Poisson process라고 이름붙입니다. 정확한 정의는 다음과 같습니다. (출처 : DeGroot, Probability and Statistics, 4ed , definition 5.4.2)
어떤 사건에 대한 단위시간당 발생비율이 $\lambda$인 Poisson process는 다음의 두 조건을 만족시키는 (stochastic) process입니다.

• 길이가 $\lambda t$인 시간간격 동안 사건이 일어나는 횟수는 Poisson distribution을 따르고, 그 평균이 $\lambda t$입니다.
• 겹치지 않는 두 개의 시간간격에 대하여 사건이 일어난 횟수는 독립적입니다.

4.8 exponential distribution

exponential distribution을 따르는 확률변수 $X$가 PDF와 평균, 분산을

\[\begin{align*} f_X(x)&=\lambda e^{-\lambda x}\qquad(x\ge0)\\ E[X]&=\frac1\lambda\\ {\sigma_X}^2&=\frac1{\lambda^2} \end{align*}\]

와 같이 가진다는 것을 확인한 바 있습니다.

그리고

단위시간동안 평균적으로 $\lambda$번의 사건이 일어난다고 기대될 때, 사건이 발생하기까지의 시간

을 $X$라고 하면, $X$는 exponential distribution을 따릅니다. 다시 말해, $X$가 위의 식을 PMF로 가집니다. 이것은 이따가 Poisson disribution과의 관계를 통해 증명하겠습니다.

Bernoulli trial의 근원사건들의 의미를 죽음(death)과 생존(survival)이라고 한다면, $X$는 생존시간을 의미한다고도 볼 수 있습니다.

difference equations and differential equations

강의에서는 geometric distribution과 exponential distribution은 각각 선형대수에서의 difference equation/differential equation (차분방정식/미분방정식)과 연관이 있다고 설명합니다. G. Strang, Linear Algebra and Its Applications, 4ed와 같은 선형대수 책에서, 행렬의 대각화에 대한 활용으로 언급되는 것이

• 5.3 Difference Equations and Powers $A^k$
• 5.4 Differential Equations and $e^{\lambda t}$

입니다.

5.3에서는 difference equation에 대해 다룹니다. 가장 간단하게 생각해볼 수 있는 예는 피보나치 수열입니다. 피보나치 수열의 $k$번째 항을 $F_k$라고 쓰면

\[\begin{align*} F_{k+2}&=F_k+F_{k+1}\\ F_{k+1}&=F_{k+1} \end{align*}\]

이 성립합니다. 연속된 두 피보나치 항을 하나의 벡터로 두면 이것은

\[\begin{bmatrix} F_{k+2}\\ F_{k+1} \end{bmatrix} = \begin{bmatrix} 1&1\\ 1&0 \end{bmatrix} \begin{bmatrix} F_{k+1}\\ F_k \end{bmatrix}\]

와 같은 행렬식으로 표현될 수 있습니다. 위와 같은 식을 difference equation(점화식, 차분식, recurrence equation)이라고 합니다. 이 difference equation을 풀어 일반항을 얻는 과정에서 정사각행렬의 거듭제곱이 등장하는데, 이를 간단하게 하기 위해서 (당연히) 행렬의 대각화를 사용합니다. 그 결과로, 피보나치 수열의 일반식에는 eigenvalues들의 거듭제곱이 수반됩니다 ;

\[\begin{align*} u_k&=c_1{\lambda_1}^kx_1+c_2{\lambda_2}^kx_2\\ F_k&=c_1{\lambda_1}^k+c_2{\lambda_2}^k \end{align*}\]

5.4에서는 연립상미분방정식(system of ordinary differential equations)의 풀이에 대해 다룹니다. difference equation에서 $\lambda^n$과 같은 형태가 핵심이었던 것과 대응되게, differential equation에서는 $e^{At}$와 같은 행렬의 exponentiation이 핵심입니다. 더 깊은 의미가 있겠지만, 어쨌든 그런 의미에서 geometric distribution과 difference equation이 대응되고, exponential distribution과 differential equation이 대응된다고 하는 것 같습니다.

memoryless property

이전 강의에서 geometric distribution이 memoryless property를 가지고 있음이 설명되었습니다. exponetial distribution도 마찬가지로 momoryless property를 가진다는 내용이 강의에 이어집니다.

앞서, exponential distribution을 따르는 확률변수 $X$를 ‘생존시간’ 혹은 ‘어떤 사건이 일어나기까지의 시간’으로 해석할 수 있다고 했었습니다. 이때, $s$ 시간 안에 죽을 확률, 혹은 $s$ 시간 안에 사건이 일어날 확률은 $P(X\le s)$로 쓸 수 있을 것입니다. exponential distribution이 memoryless property를 가진다는 것은, $t$ 시점까지 어떤 일이 일어났는지와는 상관없이, 이후의 $s$ 시간 안에 죽을 확률, 혹은 $s$ 시간 안에 사건이 일어날 확률이 $P(X\le s)$와 같다는 것입니다.

이번에도 문제를 간단하게 하기 위해, $t$ 시점까지 생존했다고(사건이 발생하지 않았다고) 가정하겠습니다. 이 가정은 $X\gt t$라는 식으로 쓸 수 있습니다. 그리고 구해야 하는 확률은, $t+s$ 시점 내에 죽을(사건이 발생할) 확률입니다. 이것은 $X\le t+s$로 쓸 수 있습니다.

따라서, $t$ 시점까지 생존했다고 가정했을 때, 그 이후 $t+s$ 시점 내에 죽을 확률 ($t$ 시점까지 사건이 발생하지 않았다고 가정했을 때, 그 이후 $t+s$시점 내에 사건이 발생할 확률)은 $P(X\le t+s|X\gt t)$로 표현될 수 있습니다. 이것이 $P(X\le s)$와 같은지를 보려고 합니다.

계산에 앞서 exponential distribution에 대한 CDF를 먼저 계산해보면

\[\begin{align*} F_X(x) &=\int_0^xf_X(\tilde x)\,d\tilde x\\ &=\int_0^x\lambda e^{-\lambda\tilde x}\,d\tilde x\\ &=1-e^{-\lambda x} \end{align*}\]

입니다. 계산해보면

\[\begin{align*} P\left(X\le t+s|X>t\right) &=\frac{P\left((X\le t+s)\cap(X>t)\right)}{P(X>t)}\\ &=\frac{P\left(t<X\le t+s\right)}{1-P(X\le t)}\\ &=\frac{F_X(t+s)-F_X(t)}{1-F_X(t)}\\ &=\frac{e^{-\lambda t}-e^{-\lambda(t+s)}}{e^{-\lambda t}}\\ &=1-e^{-\lambda s}\\ &=F_X(s)\\ &=P(X\le s) \end{align*}\]

입니다. 따라서 exponential distribution에 대해서 memoryless property가 성립합니다.

relation between ED and PD

exponential distribution과 Poisson distribution 사이의 관계를 보려고 합니다. 이를 통해, 만약 $X$가

단위시간동안 평균적으로 $\lambda$번의 사건이 일어난다고 기대될 때, 사건이 발생하기까지의 시간

이면, $X$는 exponential PDF인

\[f_X(x)=\lambda e^{-\lambda x}\qquad(x\ge0)\]

를 가진다는 것을 보려고 합니다.

단위시간동안 평균적으로 $\lambda$번의 사건이 일어난다고 가정하고 $X$를 사건이 발생하기까지의 기간이라고 하겠습니다. 그러면, 길이가 $t$인 시간간격 동안에는 평균적으로 $\lambda t$번의 사건이 일어난다고 기대할 수 있습니다. 따라서, 길이가 $t$인 시간간격동안 사건이 발생한 횟수를 $K$라고 하면 $K$는 평균이 $\lambda t$인 Poisson distribution을 따릅니다. 따라서 $K$의 PMF는

\[P_K(k)=\frac{\lambda^kt^k}{k!}e^{-\lambda t}\qquad(k=0,1,2,\cdots)\]

가 됩니다.

그러면, 길이가 $t$인 시간간격동안 한번도 사건이 발생하지 않을 확률 $P(\text{no event})$은

\[P(\text{no event})=P(K=0)=P_K(0)=e^{-\lambda t}\]

이고 길이가 $t$인 시간간격동안 적어도 한 번 사건이 발생할 확률 $P(\text{at least one event})$는

\[P(\text{at least one event})=1-P(\text{no event})=1-e^{-\lambda t}\]

입니다. 그런데 $X$를 ‘사건이 발생하기까지의 기간’으로 해석하기로 했으므로

\[P(\text{at least one event})=P(X\le t)=F_X(t)\]

입니다. 다시 말해,

\[F_X(t)=1-e^{-\lambda t}\]

입니다. 이것을 친숙한 변수 $x$로 다시 쓰면

\[F_X(x)=1-e^{-\lambda x}\]

이 되고, 이걸 미분하면

\[f_X(x)=\lambda e^{-\lambda x}\]

가 얻어집니다. $\square$

다시 정리하면, 매시각마다 일정한 비율로 일어나는 어떤 사건이 있을 때,

• 사건이 일어나는 데 걸리는 시간은 exponential distribution을 따르고
• 일정한 시간간격 동안 사건이 일어난 횟수는 Poisson distribution을 따른다

고 할 수 있습니다. 또한,

• 사건들 사이의 시간간격은 exponential distribution을 따른다

고 말할 수도 있습니다.

4.9 Erlang distribution

Erlang-$k$ distribution is a generalization of expoential distribution.

어떤 사건이 발생하는 간격은 exponetial distribution을 따른다고 했었습니다. 즉, 시각 $T_1$에 처음 사건이 발생하고 그 다음 사건이 시각 $T_2$에 발생했다면 $T_2-T_1$은 exponential distribution을 따릅니다. 다시 말해, exponential distribution은 한 개의 사건발생간격과 관련있습니다.

Erlang-$2$ distribution은 두 개의 사건발생간격을 고려합니다. 시각 $T_1$에 처음 사건이 발생하고 그 다음 사건이 시각 $T_2$에 발생하며, 또 그 다음 사건이 시각 $T_3$에 발생하면, $T_3-T_1$이 따르는 분포가 $k=2$인 Erlang distribution입니다.

(물론, $T_2-T_1$ 말고도 $T_3-T_2$, $T_4-T_3$도 exponential distribution을 따릅니다. 마찬가지로 $T_3-T_1$ 말고도 $T_4-T_2$, $T_5-T_3$도 $k=2$인 Erlang distribution을 따릅니다.)

그 연장선상에서 보면 $T_4-T_1$은 Erlang-$3$ distribution을, $T_5-T_1$은 Erlang-$4$ distribution을 따른다고 말할 수 있습니다.

Erlang-$k$ distribution($k$-order Erlang distribution)의 PMF는

\[f_X(x)=\frac{\lambda^kx^{k-1}}{(k-1)!}e^{-\lambda x}\qquad x\ge0 \tag{$\ast$}\]

입니다. 이 식은 $\langle16\rangle$에서 배우는 convolution의 개념을 통해 증명할 수 있습니다. $\langle15\rangle$

gamma function

Erlang distribution의 계산을 돕기 위해 gamma function을 다음과 같이 정의합니다.

\[\Gamma(k)=\int_0^\infty x^{k-1}e^{-x}\,dx\tag{$\ast\ast$}\]

특별히 $k$가 자연수일 때 $\Gamma(k)$는 순열(팩토리얼)의 형태가 됩니다;

\[\Gamma(k)=(k-1)!\qquad(k=1,2,\cdots)\tag{$\ast\ast\ast$}\]

이것은 $k$에 대한 귀납법으로 쉽게 증명될 수 있습니다. $k=1$이면

\[\begin{align*} \Gamma(1) &=\int_0^\infty e^{-x}\,dx\\ &=\left[-e^{-x}\right]_0^\infty\\ &=1-0\\ &=0! \end{align*}\]

입니다. $k-1$인 경우의 $(\ast\ast\ast)$이 성립한다고 가정하면, 즉, $\Gamma(k-1)=(k-2)!$을 가정하면 부분적분에 의해

\[\begin{align*} \Gamma(k) &=\int_0^\infty x^{k-1}e^{-x}\,dx\\ &=\left[-x^{k-1}e^{-x}\right]_0^\infty+\int_0^\infty (k-1)x^{k-2}e^{-x}\,dx\\ &=(0-0)+(k-1)\Gamma(k-1)\\ &=(k-1)(k-2)!\\ &=(k-1)! \end{align*}\]

이 됩니다. $\square$

gamma function의 정의 ($\ast\ast$)에서 $k$는 양의 정수(자연수)로 둘 수도 있고 양의 실수로 둘 수도 있습니다. 심지어는 실수부분이 양수인 복소수로 둘 수 있다고 합니다. (출처 : wikipedia) 그런 의미에서, gamma function은 팩토리얼의 개념을 일반화한 것이라고 볼 수 있습니다. 예를 들어,

$\frac12!$을 어떻게 정의할까?

하는 질문에 $\frac12!=\Gamma(\frac32)$ 로 정의해볼 수 있는 것입니다.

이제, Erlang distribution에 관한 $(\ast)$ 식이 정말로 PDF의 역할을 하는 지 살펴보기 위해 계산해보면

\[\begin{align*} \int_0^\infty f_{X_k}(x)\,dx &=\int_0^\infty\frac{\lambda^kx^{k-1}}{(k-1)!}e^{-\lambda x}\,dx\\ &=\frac{\lambda^k}{(k-1)!}\int_0^\infty x^{k-1}e^{-\lambda x}\,dx\\ &=\frac{\lambda^k}{(k-1)!}\int_0^\infty (\lambda x)^{k-1}\cdot\frac1{\lambda^{k-1}}e^{-\lambda x}\frac1{\lambda}\,d(\lambda x)\\ &=\frac1{(k-1)!}\int_0^\infty u^{k-1}e^{-u}\,du\\ &=\frac1{(k-1)!}\Gamma(k)\\ &=1 \end{align*}\]

입니다. 평균을 계산해보면

\[\begin{align*} E[X] &=\int_0^\infty x\cdot\frac{\lambda^kx^{k-1}}{(k-1)!}e^{-\lambda x}\,dx\\ &=\frac{\lambda^k}{(k-1)!}\underline{\int_0^\infty x^ke^{-\lambda x}\,dx}\\ &=\frac{\lambda^k}{(k-1)!}\left( \left[-\frac{x^k}\lambda e^{-\lambda x}\right]_0^\infty +\frac k{\lambda}\int_0^\infty x^{k-1}e^{-\lambda x}\,dx\right)\\ &=\frac{\lambda^k}{(k-1)!}\left(0+\frac k{\lambda^{k+1}} \int_0^\infty(\lambda x)^{k-1}e^{-\lambda x}\,d(\lambda x)\right)\\ &=\frac{\lambda^k}{(k-1)!}\times\frac k{\lambda^{k+1}} \int_0^\infty u^{k-1}e^{-u}\,du\\ &=\frac{\lambda^k}{(k-1)!}\times \underline{\frac k{\lambda^{k+1}}\times\Gamma(k)}\\ &=\frac k{\lambda} \end{align*}\]

이고 분산을 계산하기 위해 $E[X^2]$를 계산해보면

\[\begin{align*} E[X^2] &=\int_0^\infty x^2\cdot\frac{\lambda^kx^{k-1}}{(k-1)!}e^{-\lambda x}\,dx\\ &=\frac{\lambda^k}{(k-1)!}\int_0^\infty x^{k+1}e^{-\lambda x}\,dx\\ &=\frac{\lambda^k}{(k-1)!}\left( \left[-\frac{x^{k+1}}{\lambda}e^{-\lambda x}\right]_0^\infty +\frac{k+1}\lambda\int_0^\infty x^ke^{-\lambda x}\,dx\right)\\ &=\frac{\lambda^k}{(k-1)!}\times\frac{k+1}\lambda\times\frac k{\lambda^{k+1}}\times\Gamma(k)\\ &=\frac{k(k+1)}{\lambda^2} \end{align*}\]

입니다. 계산과정의 세번째 줄에서 네번째 줄로 넘어가는 것은 $E[X]$의 계산에서 밑줄친 두 값이 같다는 것을 활용한 것입니다. 분산을 계산하면

\[{\sigma_{X_k}}^2=E[X^2]-E[X]^2=\frac k{\lambda^2}\]

이 됩니다.

이 결과들을 exponential distribution의 평균과 분산과의 관계와 연결지어 해석해보면 다음과 같습니다. 어떤 사건이 시각 $T_0$ $T_1$, $T_2$, $T_3$, $\cdots$, $T_k$에 일어난다고 가정할 때, $T_1-T_0$, $T_2-T_1$, $\cdots$, $T_k-T_{k-1}$은 모두 exponential distribution을 따른다고 했습니다. 반면, $T_2-T_0$, $T_3-T_1$, $\cdots$, $T_k-T_{k-2}$는 Erlang-$2$ distribution을 따릅니다. 마찬가지로, $T_3-T_0$, $T_4-T_1$, $\cdots$, $T_k-T_{k-3}$는 Erlang-$3$ distribution을 따릅니다. 그리고 $T_k-T_0$는 Erlang-$k$ distribution을 따른다고 했습니다.

그러면, exponential distribution을 따르는 두 확률분포를 더하면 그것은 Erlang-$2$ distribution을 따른다고 볼 수 있습니다;

\[(T_1-T_0)+(T_2-T_1)=T_2-T_0\]

그리고, exponential distribution을 따르는 $k$개의 확률분포를 더하면 그것은 Erlang-$k$ distribution을 따른다고 볼 수 있습니다;

\[(T_1-T_0)+(T_2-T_1)+\cdots+(T_k-T_{k-1})=T_k-T_0\]

만약, exponential distribution을 따르는 각각의 확률변수들을

\[T_1-T_0=X^{(1)},\quad T_2-T_1=X^{(2)},\quad \cdots,\quad T_k-T_{k-1}=X^{(k)}\]

으로 표기하고 $X_k=T_k-T_0$이라고 하면,

\[X^{(1)}+X^{(2)}+\cdots+X^{(k)}=X_k\]

인 것입니다. 따라서

\[\begin{align*} E[X_k] &=E\left[X^{(1)}+X^{(2)}+\cdots+X^{(k)}\right]\\ &\stackrel{\star}=E[X^{(1)}]+E[X^{(2)}]+\cdots+E[X^{(k)}]\\ &=\frac1\lambda+\frac1\lambda+\cdots+\frac1\lambda\\ &=\frac k\lambda. \end{align*}\]

라고 생각할 수 있습니다. 이것은 아까 계산한 Erlang-$k$ distribution의 평균과 정확히 일치합니다. 여기에서 $(\star)$의 과정은 직관적으로는 당연하지만, 엄밀하게는 아직 논할 수 없습니다. 그리고 ‘각 사건의 발생이 독립적이다’와 같은 가정이 있어야 저 과정이 정당화될 수 있을 것입니다.

강의에서는 나중에 convolution의 개념을 배우고 나서 저 $(\star)$ 과정을 제대로 설명할 수 있다고 말합니다. 그런데 정말로 그런 것이, 만약 $X^{(i)}$들이 0과 자연수의 값을 가진다고 가정하고(discrete) $X_2=T_2-T_0=X^{(1)}+X^{(2)}$의 PMF를 $X^{(1)}$의 PMF와 $X^{(2)}$의 PMF로 구하려고 한다면

\[\begin{align*} P_{X_2}(x) &=P(X_2=x)\\ &=P(X^{(1)}+X^{(2)}=x)\\ &=P\left((X^{(1)}=0)\cap(X^{(2)}=x)\right) +P\left((X^{(1)}=1)\cap(X^{(2)}=x-1)\right) +\cdots +P\left((X^{(1)}=x)\cap(X^{(2)}=0)\right)\\ &=\sum_{i=1}^xP\left((X^{(1)}=i)\cap(X^{(2)}=x-i)\right)\\ &=\sum_{i=1}^xP(X^{(1)}=i)\times P(X^{(2)}=x-i)\\ &=\sum_{i=1}^xP_{X^{(1)}}(i)\times P_{X^{(2)}}(x-i)\\ \end{align*}\]

와 같은 꼴이 되어, $P_{X_2}$가 $P_{X^{(1)}}$와 $P_{X^{(1)}}$의 convolution 형태로 나타나기 때문인 것 같습니다. (exponential distribution과 Erlang distribution의 원래 정의에서처럼 PDF로 계산하는 경우에는 summation이 아닌 적분과 관련된 식으로 convolution 식이 나옵니다.)

분산에 대해서도 비슷한 해석을 할 수 있다고 하는데, 사실 강의에서의 설명은 잘 이해하지는 못했습니다. 하지만, 다음과 같이 해석하면 되지 않을까 싶습니다. $X^{(1)}$, $X^{(2)}$, $\cdots$, $X^{(k)}$가 모두 평균 $\mu$를 가지고 분산 $\sigma^2$를 가지는 동일한 분포를 따를 때, 이것들의 산술평균인 $\overline X = \frac1k(X^{(1)}+\cdots+X^{(k)})$는 평균이 $\mu$이고 분산이 $\frac{\sigma^2}k$임이 알려져있습니다(표본평균의 평균과 분산). 그러니까,

\[\begin{align*} \sigma_{X_k} &=V[X_k]\\ &=V[X^{(1)}+X^{(2)}+\cdots X^{(k)}]\\ &=V[k\overline X]\\ &=k^2V[\overline X]\\ &=k^2\times\frac{\sigma^2}k\\ &=k\sigma^2\\ &=kV[X^{(1)}]\\ &=\frac{k}{\lambda^2} \end{align*}\]

이 되어 앞서 계산의 결과와 일치합니다.

마지막으로, $X_k$의 CDF를 계산해봅니다. 이 계산은 gamma function을 직접적으로 사용할 수 없습니다. wikipedia 등에 따르면 위에서 정의한 gamma function에서 더 나아간 incomplete gamma function 과 같은 함수를 사용하면 $X_k$의 CDF를 계산하는 것이 더 쉬워지는 것으로 보이는데, 여기에서는 그냥 부분적분과 귀납법을 사용해 계산하겠습니다. 실제 강의에서도 부분적분을 연속적으로 사용하여 계산할 수 있다고 언급되고 있습니다.

\[\begin{align*} F_{X_k}(x) &=\int_0^xf_{X_k}(t)\,dt\\ &=\int_0^x\frac{\lambda^kt^{k-1}}{(k-1)!}e^{-\lambda t}\,dt\\ &=\frac{\lambda^k}{(k-1)!}\int_0^xt^{k-1}e^{-\lambda t}\,dt\\ &=\frac1{(k-1)!}\int_0^{\lambda x}(\lambda t)^{k-1}e^{-\lambda t}\,d(\lambda t)\\ &=\frac1{(k-1)!}\int_0^{\lambda x}u^{k-1}e^{-u}\,du\\ &\stackrel{\star\star}=1-\sum_{n=0}^{k-1}\frac{(\lambda x)^n}{n!}e^{-\lambda x} \end{align*}\]

$\star\star$를 수학적 귀납법으로 증명하겠습니다. $k=1$인 경우는

\[\begin{align*} \text{LHS} &=\frac1{0!}\int_0^{\lambda x}u^0e^{-u}\,du\\ &=\left[-e^{-u}\right]_0^{\lambda x}\\ &=1-e^{-\lambda x}\\ &=1-\sum_{n=0}^0\frac{(\lambda x)^n}{n!}e^{-\lambda x}\\ &=\text{RHS} \end{align*}\]

가 되어 성립합니다. $k$의 경우를 성립한다고 가정하고 $k+1$인 경우를 고려하면

\[\begin{align*} \text{LHS} &=\frac1{k!}\int_0^{\lambda x}u^ke^{-u}\,du\\ &=\frac1{k!}\left(\left[-u^ke^{-u}\right]_0^{\lambda x} +k\int_0^{\lambda x}u^{k-1}e^{-u}\,du\right)\\ &=-\frac1{k!}(\lambda x)^ke^{-\lambda x} +\frac1{(k-1)!}\int_0^{\lambda x}u^{k-1}e^{-u}\,du\\ &=-\frac{(\lambda x)^k}{k!}e^{-\lambda x} +1-\sum_{n=0}^{k-1}\frac{(\lambda x)^n}{n!}e^{-\lambda x}\\ &=1-\sum_{n=0}^k\frac{(\lambda x)^n}{n!}e^{-\lambda x}\\ &=\text{RHS} \end{align*}\]

입니다. $\square$

4.10 uniform distribution

uniform distribution에 대해서도 이미 다룬 바가 있지만, 이번에는 PMF와 PDF, 평균과 분산에 대해 다시 봅니다.

$X$가 uniform한 이산확률분포이고 $X$가 가질 수 있는 값이 $x_1$, $x_2$, $\cdots$, $x_n$이면, 즉

\[X\sim\text{Unif}(x_1,x_2,\cdots,x_n)\]

이면, $P(X=x_1)=P(X=x_2)=\cdots=P(X=x_n)$으로부터

\[P_X(x_i)=\frac1n\qquad(i=1,2,\cdots,n)\]

로 $X$의 PMF가 결정됩니다. 만약 $X$가 uniform한 연속확률분포이고 $X$가 가질 수 있는 값이 $a\le X\le b$이면, 즉

\[X\sim\text{Unif}\left([a,b]\right)\]

이면,

\[f_X(x)=c(a\le x\le b)\]

이고

\[\int_a^bf_X(x)\,dx=1\]

로부터

\[f_X(x)=\frac1{b-a}(a\le x\le b)\]

입니다.

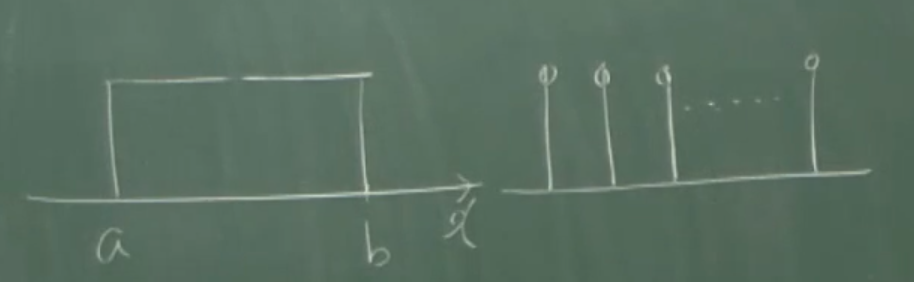
이산확률분포의 경우 $E[X]=\frac1n(x_1+\cdots+x_n)$, ${\sigma_X}^2=\frac1n\left(\sum_i(x_i-\mu_X)^2\right)$이어서 새로울 게 없습니다. 연속확률 변수의 경우의 평균과 분산은 $E[X]=\frac{a+b}2$, ${\sigma_X}^2=\frac{(a-b)^2}{12}$로 주어지는데, 직접 계산해보면

\[\begin{align*} E[X] &=\int_a^bxf_X(x)\,dx\\ &=\frac 1{b-a}\int_a^bx\,dx\\ &=\frac{a+b}2\\ {\sigma_X}^2 &=\int_a^bx^2f_X(x)\,dx-E[X]^2\\ &=\frac 1{b-a}\int_a^bx^2\,dx-\left(\frac{a+b}2\right)^2\\ &=\frac{a^2+ab+b^2}3-\frac{a^2+2ab+b^2}4\\ &=\frac{a^2-2ab+b^2}{12}\\ &=\frac{(a-b)^2}{12} \end{align*}\]

입니다. 강의의 마지막에는 앞서 언급된 적이 있었던 digitization에서의 quantization에 대한 설명이 다시 나옵니다. quantization에서의 level 사이의 간격을 $\Delta$라고 할 때, quantization error $e$는

\[-\frac\Delta2\lt e\le\frac\Delta2\]

와 같이 주어질텐데, 이때 $e$가 $[-\frac\Delta2,\frac\Delta2]$에서의 uniform distribution을 따른다고 가정한다는 것입니다. 그러면 $e$의 분산은

\[V[e]=\frac{\Delta^2}{12}\]

으로 나타나게 될 것입니다. 이때, error의 분산은 전력(power, 평균 에너지의 크기)로 해석할 수 있다고 합니다. 신호의 실제값들의 표준편차를 $\sigma_S$라고 하면,

\[\log_{10}\left(\frac{\,{\sigma_S}^2}{\left(\frac\Delta{12}\right)^2}\right)\]

은 SNR(신호 대 잡음비)의 값으로 정의할 수 있는데, 이 값은 db(데시벨)이라는 단위를 가지고 있다고 합니다.

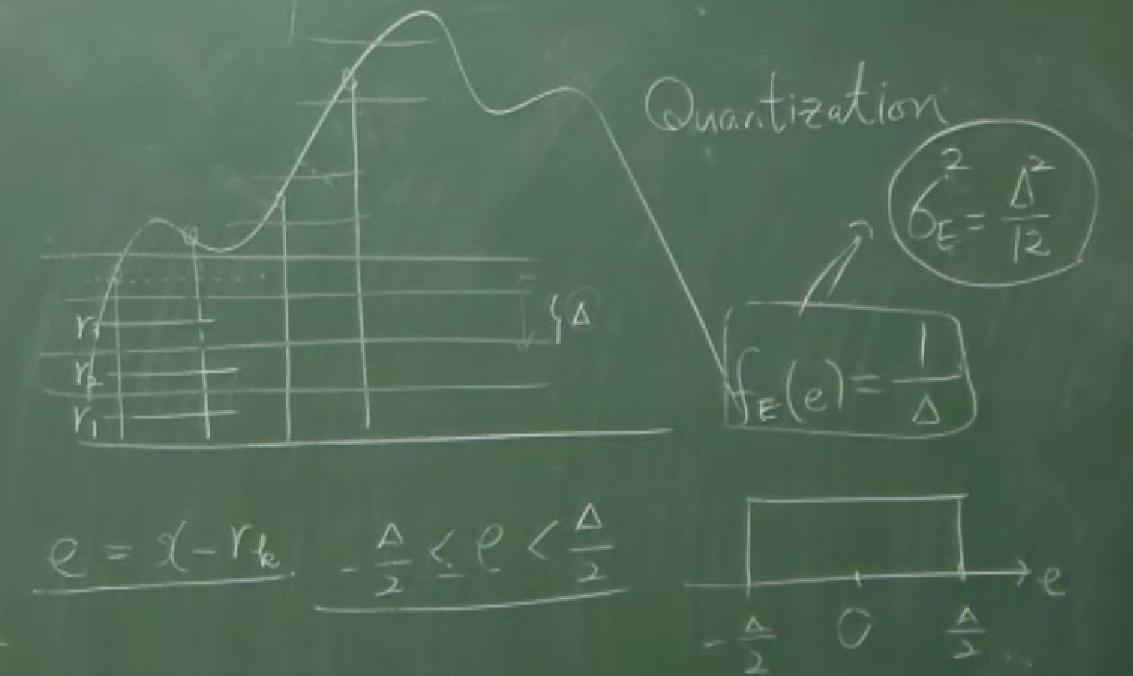
09 정규분포

연속확률변수 $X$가 확률밀도함수

\[\tag{$\ast$} f_X(x)=\frac1{\sqrt{2\pi}\sigma_X}e^{-\frac{(x-{\mu_X})^2}{2{\sigma_X}^2}} \qquad(-\infty\lt x\lt\infty)\]

를 가지면 $X$가 정규분포를 따른다고 하고 $X\sim N(\mu_X,{\sigma_X}^2)$라고 표시합니다. 이 PDF에 대하여 다음 세 사실이 성립합니다.

\[\begin{aligned} \int_{-\infty}^\infty f_X(x)\,dx&=1\\ E[X]&=\mu_X\\ V[X]&={\sigma_X}^2 \end{aligned} \tag{$\ast\ast$}\]

이것을 직접 증명하는 것은 복잡하기 때문에, 먼저 $\mu=0$이고 $\sigma=1$인 경우를 보려고 합니다(standard normal distribution). 다시 말해,

\[f_U(u)=\frac1{\sqrt{2\pi}}e^{-\frac12u^2} \qquad(-\infty\lt x\lt\infty)\]

로 주어진 연속확률변수 $U$에 대하여

\[\begin{aligned} \int_{-\infty}^\infty f_U(u)\,du&=1\\ E[U]&=0\\ V[U]&=1 \end{aligned} \tag{$\ast\ast\ast$}\]

를 증명하려고 합니다.

먼저 $U$의 확률밀도함수를 실수 전체에 대해 적분했을 때 1이 된다는 사실을 먼저 증명하기 위해

\[A=\int_{-\infty}^\infty f_U(u)\,du\]

로 두면, 극좌표계 변환에 의해

\[\begin{align*} A^2 &=\int_{-\infty}^\infty\frac1{\sqrt{2\pi}}e^{-\frac12u^2}\,du\times \int_{-\infty}^\infty\frac1{\sqrt{2\pi}}e^{-\frac12v^2}\,dv\\ &=\frac1{2\pi}\iint_{\mathbb R^2}e^{-\frac12(u^2+v^2)}\,du\,dv\\ &=\frac1{2\pi}\int_0^{2\pi}\int_0^\infty e^{-\frac12r^2}r\,dr\,d\theta\\ &=\frac1{2\pi}\int_0^{2\pi}d\theta\times \int_0^\infty e^{-\frac12r^2}r\,dr\\ &=\frac1{2\pi}\times 2\pi\times\int_0^\infty e^{-\frac12r^2}\,d\left(\frac12r^2\right)\\ &=\int_0^\infty e^{-R}\,dR\\ &=\left[-e^R\right]_0^\infty\\ &=1 \end{align*}\]

입니다. 따라서 $A=1$입니다.

$U$의 평균을 계산하기 위해 똑같이 해보면

\[\begin{align*} E[U]^2 &=\int_{-\infty}^\infty\frac u{\sqrt{2\pi}}e^{-\frac12u^2}\,du\times \int_{-\infty}^\infty\frac v{\sqrt{2\pi}}e^{-\frac12v^2}\,dv\\ &=\frac1{2\pi}\iint uve^{-\frac12(u^2+v^2)}\,du\,dv\\ &=\frac1{2\pi}\int_0^{2\pi}\int_0^\infty r^2\cos\theta\sin\theta e^{-\frac12r^2}r\,dr\,d\theta\\ &=\frac1{2\pi}\int_0^{2\pi}\cos\theta\sin\theta\,d\theta\times \int_0^\infty r^3e^{-\frac12r^2}\,dr\\ &=\frac1{2\pi}\int_0^{2\pi}\frac12\sin(2\theta)\,d\theta \times\int_0^\infty \left(\frac12r^2\right)e^{-\frac12r^2}\,d\left(\frac12r^2\right)\times2\\ &=\frac1{2\pi}\times\left[-\frac14\cos(2\theta)\right]_0^{2\pi}\times \int_0^\infty Re^{-R}\,dR\times2\\ &=\frac1{2\pi}\times0\times1\times2\\ &=0 \end{align*}\]

입니다. 따라서 $E[U]=0$입니다.

마지막으로 $U$의 분산을 계산해보면

\[\begin{align*} V[U] &=\int_{-\infty}^\infty\frac{(u-0)^2}{\sqrt{2\pi}}e^{-\frac12u^2}\,du\\ &=\int_{-\infty}^\infty\frac{u^2}{\sqrt{2\pi}}e^{-\frac12u^2}\,du \end{align*}\]

이고

\[\begin{align*} V[U]^2 &=\int_{-\infty}^\infty\frac{u^2}{\sqrt{2\pi}}e^{-\frac12u^2}\,du\times \int_{-\infty}^\infty\frac{v^2}{\sqrt{2\pi}}e^{-\frac12v^2}\,dv\\ &=\frac1{2\pi}\iint u^2v^2e^{-\frac12(u^2+v^2)}\,du\,dv\\ &=\frac1{2\pi}\int_0^{2\pi}\int_0^\infty r^4\cos^2\theta\sin^2\theta e^{-\frac12r^2}r\,dr\,d\theta\\ &=\frac1{2\pi}\int_0^{2\pi}\cos^2\theta\sin^2\theta\,d\theta\times \int_0^\infty r^5e^{-\frac12r^2}\,dr\\ &=\frac1{2\pi}\int_0^{2\pi}\frac14\sin^2(2\theta)\,d\theta \times\int_0^\infty \left(\frac12r^2\right)^2e^{-\frac12r^2}\,d\left(\frac12r^2\right)\times4\\ &=\frac1{2\pi}\int_0^{2\pi}\frac18(1-\cos(4\theta))\,d\theta\times \int_0^\infty R^2e^{-R}\,dR\times4\\ &=\frac1{2\pi}\times\frac\pi4\times2\times4\\ &=1 \end{align*}\]

따라서 $(\ast\ast\ast)$가 증명되었습니다. 이제 $(\ast\ast)$를 증명해보려고 합니다. 만약 확률변수 $X$가 $(\ast)$를 PDF로 가진다면 변수변환 $x=\sigma_Xu+\mu_X$에 의하여

\[\begin{align*} \int_{-\infty}^\infty f_X(x)\,dx &=\int_{-\infty}^\infty\frac1{\sqrt{2\pi}\sigma_X}e^{-\frac{(x-{\mu_X})^2}{2{\sigma_X}^2}}\,dx\\ &=\int_{-\infty}^\infty\frac1{\sqrt{2\pi}}e^{-\frac12u^2}\,du\\ &=1 \end{align*}\]

입니다. 따라서 $(\ast\ast\ast)$의 첫번째 식이 증명되었습니다. 또한, 새로운 확률변수

\[U=\frac{X-\mu_X}{\sigma_X}\]

는 standard normal입니다. ($U\sim N(0,1)$ 입니다.) 왜냐하면,

\[\begin{align*} F_U(u) &=P(U\le u)\\ &=P(\frac{x-\mu_X}{\sigma_X}\le u)\\ &=P(X\le\sigma_Xu+\mu_X)\\ &=F_X\left(\sigma_Xu+\mu_X\right)\\ f_U(u) &=\frac d{du}F_U(u)\\ &=\frac d{du}F_X\left(\sigma_Xu+\mu_X\right)\\ &=\sigma_Xf_X\left(\sigma_Xu+\mu_X\right)\\ &=\sigma_X\times\frac1{\sqrt{2\pi}\sigma_X}e^{-\frac12\left(\frac{x-\mu_X}{\sigma_X}\right)^2}\\ &=\frac1{\sqrt{2\pi}}e^{-\frac12\left(\frac{x-\mu_X}{\sigma_X}\right)^2} \end{align*}\]

이기 때문입니다. 따라서

\[\begin{align*} E[X] &=E\left[\mu_X+\sigma_XU\right]\\ &=\mu_X+\sigma_XE[U]\\ &=\mu_X\\ {\sigma_X}^2 &=V\left[\mu_X+\sigma_XU\right]\\ &={\sigma_X}^2V[U]\\ &={\sigma_X}^2 \end{align*}\]

입니다. 즉 $(\ast\ast)$의 나머지 두 식이 증명되었습니다. $\square$

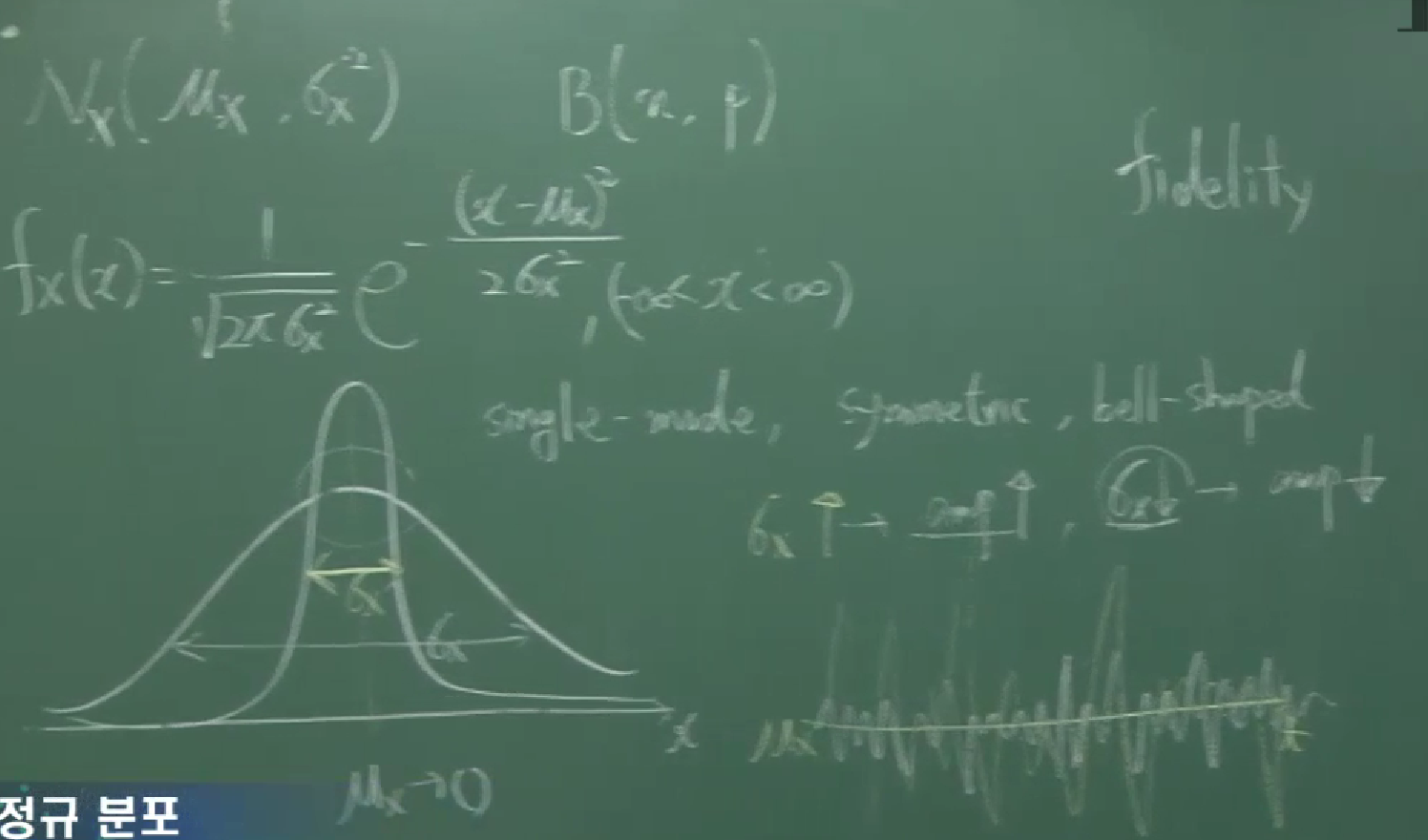
강의에서는 여러 종류의 연속확률변수들이 근사적으로 정규분포를 따른다는 것이 언급되면서, 특히 어떤 신호의 signal이 정규분포를 따르는 경향이 있다는 사실도 소개됩니다. single mode, symmetric, bellshaped등의 성질들에 대해서도 언급됩니다.

여기에서 mode란 PDF의 극대점을 의미한다고 설명되고 있습니다. discrete case에서는 mode가 최빈값, 즉 PMF의 최대점을 의미합니다.

강의에서 위의 계산도 하는 것 같은데, $du\,dv=r\,dr\,d\theta$를 설명하기 위해 Jacobian matrix도 소개되고 있습니다. 다만 위에서 계산한 세 값 중 맨 위의 값만 계산하고 있습니다.

이외에도 표준정규분포, 표준정규분포표에 대해서도 소개되고 있습니다. 이때 $\Phi$를 표준정규분포의 CDF로 정합니다. 즉, $Z\sim N(0,1)$일 때,

\[\Phi(x)=F_Z(x)=P(Z\le x)=\int_{-\infty}^x\frac1{\sqrt{2\pi}}e^{-\frac{z^2}2}\,dz\]

로 정의합니다.

approximation of binomial distributions

$X\sim B(n,p)$이고 $n$이 충분히 크면 $X\sim N(np,np(1-p))$으로 생각합니다.

error function

\[\text{erf}(x)=\frac2{\sqrt\pi}\int_0^xe^{-y^2}\,dy.\]

$X\sim N(0,\frac12)$이면, 이 함수는 $\text{er}f(x)=P(-x\lt X\le x)$인 함수입니다.

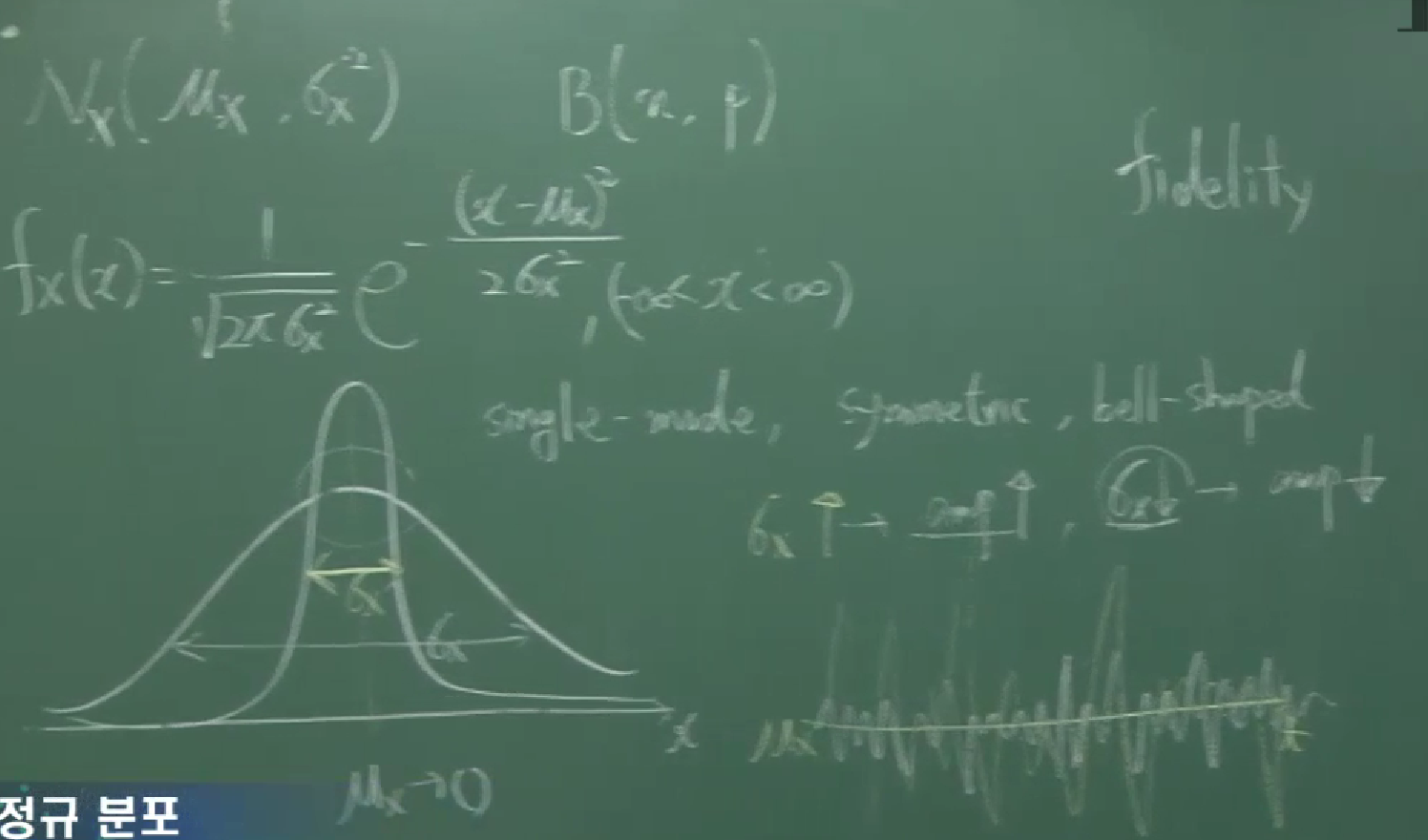
complementary error function

\[\text{erfc}(x)=\frac2{\sqrt\pi}\int_x^\infty e^{-y^2}\,dy.\]

$\text{erfc}$ 함수는 $\text{erf}$ 함수와 complementary한 관계가 있습니다. 다시 말해서

\[\text{erf}(x)+\text{erfc}(x)=1\]

입니다.

또한,

\[\begin{align*} \text{erf}(x) &=2P(0\le X\le x)\\ &=2P\left(0\le Z\le\sqrt2x\right)\\ &=2\left(\Phi(\sqrt2x)-\frac12\right)\\ &=2\Phi(\sqrt2x)-1 \end{align*}\]

이고, 반대로

\[\Phi(x)=\frac12+\frac12\text{erf}\left(\frac{x}{\sqrt2}\right)\]

입니다.

Gaussian mixture model

$X_1\sim N(\mu_1,{\sigma_1}^2)$, $X_2\sim N(\mu_2,{\sigma_2}^2)$일 때,새로운 확률변수 $\alpha X_1+\beta X_2$는 하나의 mode를 가지지 않고 두 개의 mode를 가질 수 있습니다(bimodal). 일반적으로, 서로 다른 정규분포를 따르는 $n$개의 확률변수 $X_i$에 대하여 $X_i$들의 일차결합은 여러 개의 mode를 가질 수 있습니다(multimodal). 이 확률변수를 가지고 만들 수 있는 모델을 Gaussian mixture model이라고 하는 것 같습니다. sklearn에서는 다음과 같은 설명을 하고 있습니다.

A Gaussian mixture model is a probabilistic model that assumes all the data points are generated from a mixture of a finite number of Gaussian distributions with unknown parameters.

4.5 Pascal distribution (Negative binomial distribution)

강의의 마지막에는 Pascal distribution에 대한 설명이 간략하게 있습니다. 이에 관해서는 칠판에 적힌 캡쳐로 간단하게 갈음하겠습니다.

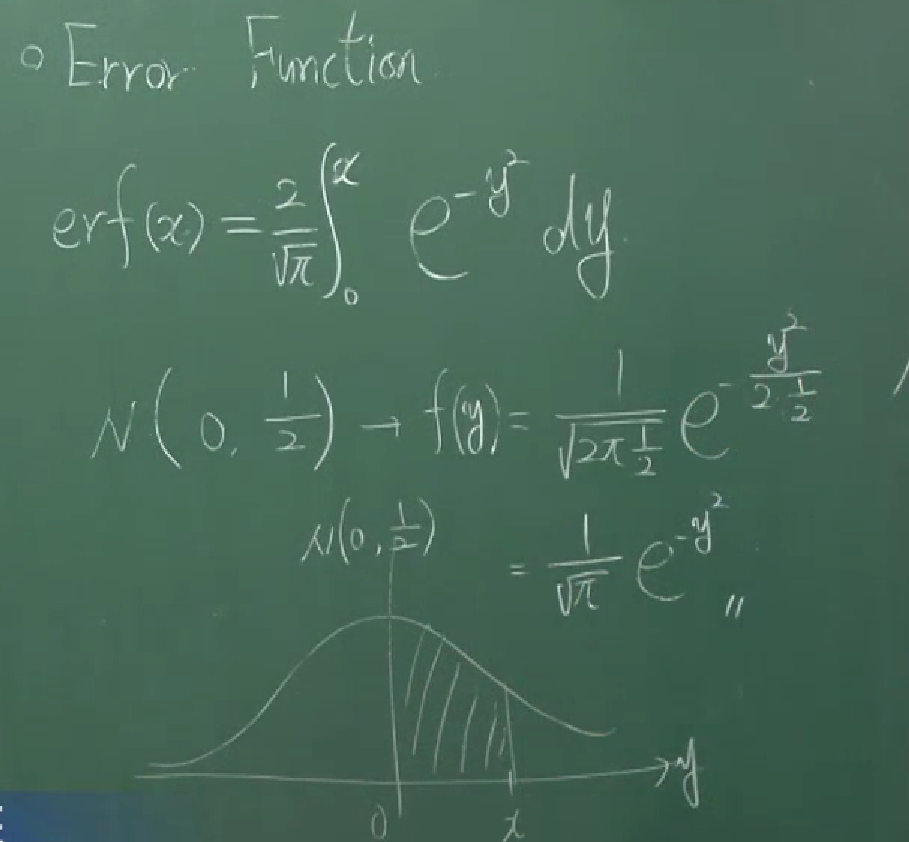
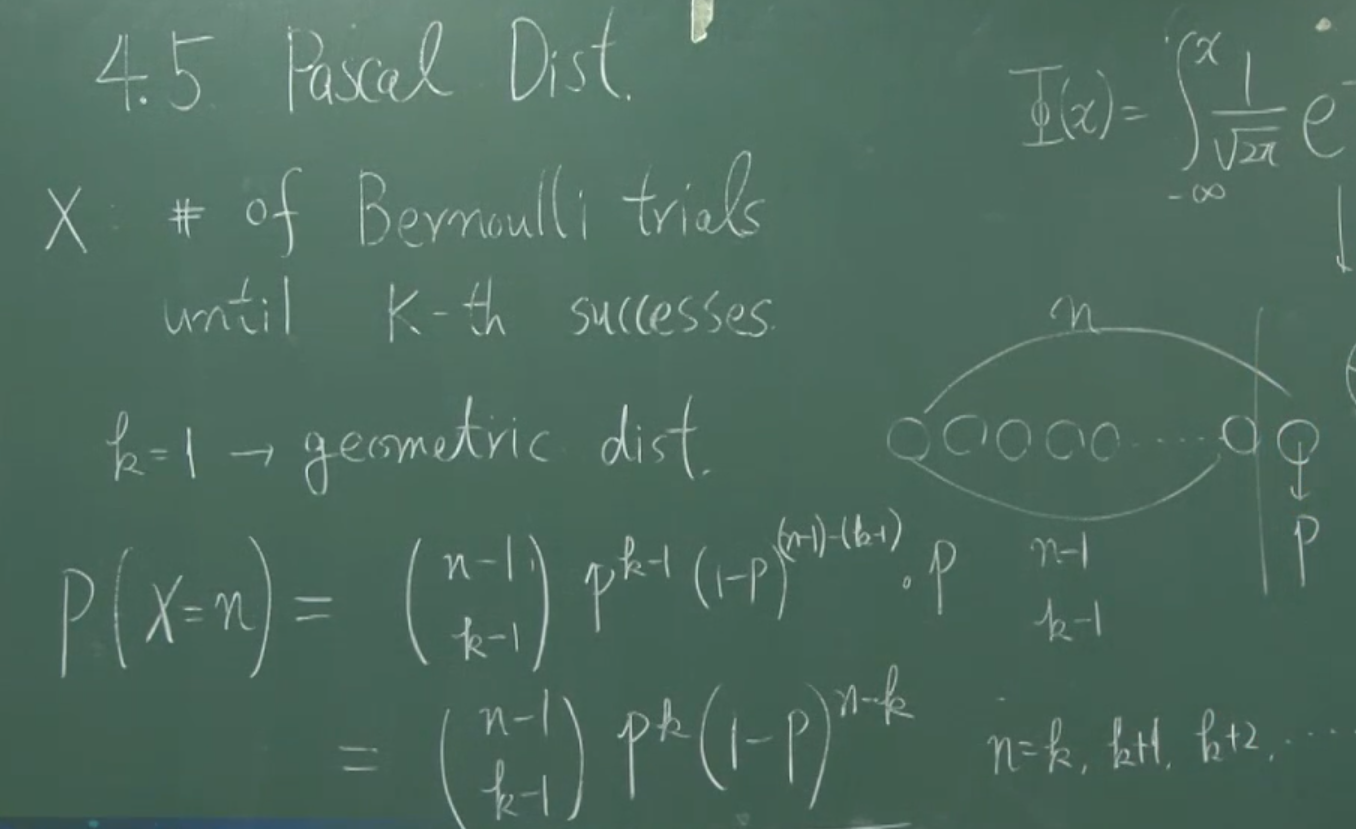
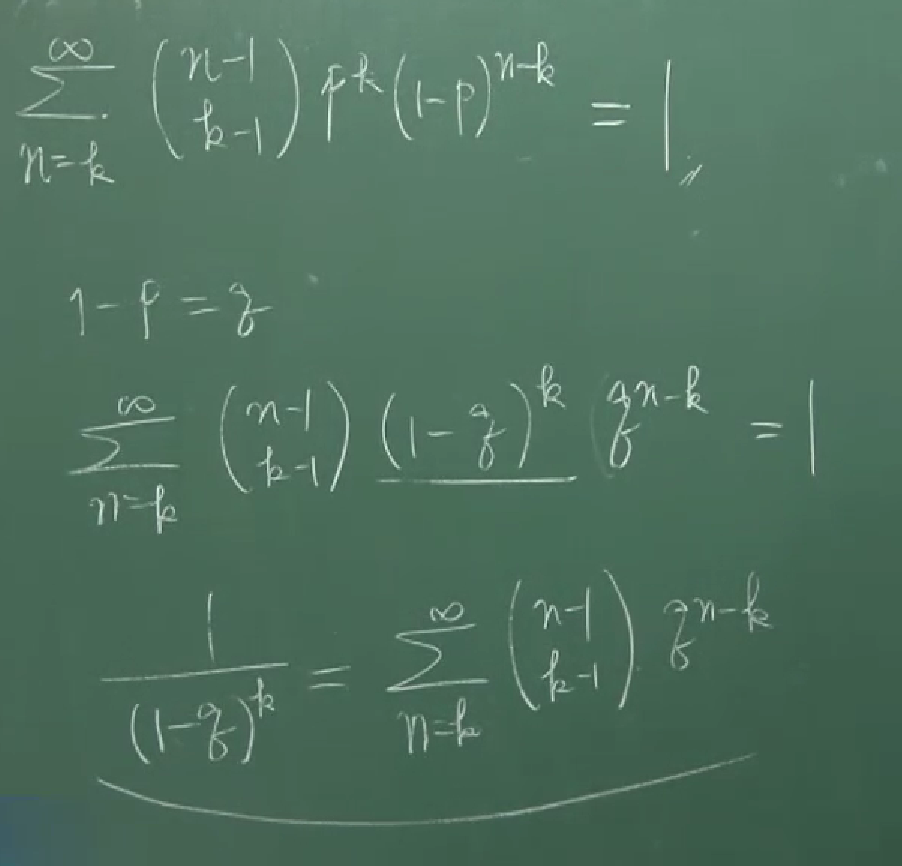
강의의 내용은 여기까지입니다. 하지만, 정규분포가 워낙 중요한 분포이고 나중에 사용할 수 있는 중요한 성질들이 언급되어있지 않기 때문에, 조금 더 적어보려고 합니다. 여기에 적어볼 사실은 다음과 같습니다.

(a) $X\sim N(\mu,\sigma^2)\qquad\iff\qquad M_X(t)=\exp\left(\mu t+\frac12\sigma^2t^2\right)$
(b) 두 확률변수 $X\sim N(\mu_X,{\sigma_X}^2)$, $Y\sim N(\mu_Y,{\sigma_Y}^2)$ 가 독립이면 $$aX+bY+c\sim N\left(a\mu_X+b\mu_Y+c,a^2{\sigma_X}^2+b^2{\sigma_Y}^2\right).$$ 이 성립합니다.

(a)에서 등장하는 $M_X$라는 함수는 moment generating function이라고 불립니다. 즉 (a)의 내용은, 정규분포가 moment generating function을 통해 설명(characterize)될 수 있다는 것입니다. (b)는 정규분포를 따르며 독립인 확률변수들의 일차결합이 여전히 정규분포를 따른다는 중요한 사실을 이야기하고 있습니다. 이것들에 대한 증명을 시작하기 전에, 먼저 moment generating function에 대해 간략하게 설명해보겠습니다.

moment genrating functions
$X$가 확률변수일 때, $$M_X(t)=E\left[e^{tX}\right]$$ 를 $X$의 moment generating function이라고 합니다. 이것을 활용하면, $X$의 $n$th moment를 쉽게 계산할 수 있습니다; $${M_X}^{(n)}(0)=E[X^n]$$

이에 대한 증명은 다음과 같습니다. 아래 계산에서 등장하는 급수들은 모두 적당히 잘 수렴한다고 가정합니다. $e^{tX}$에 Maclaurin series를 적용하면

\[\begin{align*} M_X(t) &=E\left[e^{tX}\right]\\ &=E\left[1+tX+\frac{t^2X^2}{2!}+\frac{t^3X^3}{3!}+\cdots\right]\\ &=1+tE[X]+\frac{t^2}{2!}E[X^2]+\frac{t^3}{3!}E[X^3]+\cdots \end{align*}\]

입니다. 따라서

\[\begin{align*} M_X'(t)&=E[X]+tE[X^2]+\frac{t^2}{2!}E[X^3]+\frac{t^3}{3!}E[X^4]+\cdots\\ M_X''(t)&=E[X^2]+tE[X^3]+\frac{t^2}{2!}E[X^4]+\frac{t^3}{3!}E[X^5]+\cdots\\ &\vdots\\ M_X^{(n)}(t)&=E[X^n]+tE[X^{n+1}]+\frac{t^2}{2!}E[X^{n+2}]+\frac{t^3}{3!}E[X^{n+3}]+\cdots. \end{align*}\]

이고

\[M_X^{(n)}(0)=E[X^n].\]

입니다. $\square$

Uniqueness of moment generating function
확률변수 $X$에 대하여 그에 대응하는 moment generating function $M_X$는 유일(unique)하다고 알려져있습니다. 다시 말해, 새로운 확률변수 $X'$이 $M_X=M_{X'}$을 만족시키면, $X$와 $X'$의 분포는 같습니다. 이에 대한 증명은 생략하겠지만, 이 사실은 매우 유용하게 쓰일 수 있습니다.

이제 (a)를 증명해보겠습니다. 먼저 $\Rightarrow$ 방향입니다.

$X\sim N(\mu,\sigma^2)$를 가정하면

\[\begin{align*} M_X(t) &=E[e^{tX}]\\ &=\int_{\mathbb R}e^{tx}\times\frac1{\sqrt{2\pi}\sigma}\exp\left(-\left(\frac{x-\mu}{\sqrt2\sigma}\right)^2\right)\,dx\\ &=\frac1{\sqrt{2\pi}\sigma}\int_{\mathbb R}\exp\left(tx-\left(\frac{x-\mu}{\sqrt2\sigma}\right)^2\right)\,dx. \end{align*}\]

입니다.

변수변환 $u=\frac{x-\mu}{\sqrt2\sigma}$ 을 하면 $dx=\sqrt2\sigma\,du$ 이므로

\[\begin{align*} M_X(t) &=\frac1{\sqrt{2\pi}\sigma}\int_{\mathbb R}\exp\left(t(\mu+\sqrt2\sigma u)-u^2\right)\times\sqrt2\sigma\,du.\\ &=\frac{e^{\mu t}}{\sqrt\pi}\int_{\mathbb R}\exp\left(\sqrt2\sigma tu-u^2\right)\,du.\\ &=\frac{e^{\mu t}}{\sqrt\pi}\int_{\mathbb R}\exp\left(-\left(u-\frac{\sigma t}{\sqrt2}\right)^2+\frac{\sigma^2t^2}2\right)\,du.\\ \end{align*}\]

입니다. 다시, 변수변환 $v=u-\frac{\sigma t}{\sqrt2}$를 적용하면

\[\begin{align*} M_X(t) &=\frac{e^{\mu t+\frac12\sigma^2t^2}}{\sqrt\pi}\int_{\mathbb R}\exp\left(-v^2\right)\,du\\ &\stackrel{\star}=\frac{e^{\mu t+\frac12\sigma^2t^2}}{\sqrt\pi}\times\sqrt\pi\\ &=e^{\mu t+\frac12\sigma^2t^2}. \end{align*}\]

이 됩니다. 이때, $\star$는 $\langle09\rangle$의 서두에 등장했던 이중적분과 좌표변환을 통해 얻을 수 있습니다.

(a)의 반대방향($\Leftarrow$)은 $M_X$가 유일하다는 것으로부터 당연합니다. 즉, 만약 확률변수 $Y$가 $M_Y(t)=\exp\left(\mu t+\frac12\sigma^2t^2\right)$를 만족시키는 확률변수여서 (a)의 오른쪽 조건이 성립한다면, $M_X=M_Y$가 성립합니다. 그런데 moment generating function의 유일성으로부터 $Y$와 $X$의 분포는 같습니다. 그러므로 $Y\sim N(\mu,\sigma^2)$이고, (a)의 왼쪽조건이 성립합니다. 따라서 (a)의 $\Leftarrow$ 방향도 증명되었습니다.

이번엔 (b)에 대한 증명입니다. (a)의 $\Rightarrow$방향과 moment generating function의 정의, 그리고 독립인 확률변수들의 성질로부터

\[\begin{align*} M_{aX+bY+c}(t) &=E\left[e^{(aX+bY+c)t}\right]\\ &=E\left[e^{aXt}e^{aYt}e^{ct}\right]\\ &\stackrel{\star\star}=E\left[e^{X(at)}\right]E\left[e^{Y(bt)}\right]E\left[e^{ct}\right]\\ &=M_X(at)\times M_Y(bt)\times e^{ct}\\ &=\exp\left(\mu_X(at)+\frac12{\sigma_X}^2(at)^2\right)\times\exp\left(\mu_Y(bt)+\frac12{\sigma_Y}^2(bt)^2\right)\times\exp(ct)\\ &=\exp\left((a\mu_X+b\mu_Y+c)t+\frac12\left(a^2{\sigma_X}^2+b^2{\sigma_Y}^2\right)t^2\right) \end{align*}\]

입니다. 이때 $\star\star$는 $X$와 $Y$가 독립이라는 사실 때문에 그렇습니다. 즉, 두 함수 $f$, $g$에 대하여

\[E[f(X)g(Y)]=E[f(X)]E[g(Y)]\]

가 성립하는데, 이것은 $\langle12\rangle$에서 증명됩니다. 다시 증명으로 돌아와보면, (a)의 $\Leftarrow$ 방향으로부터 $aX+bY+c$가 평균이 $a\mu_X+b\mu_Y+c$ 이고 분산이 $a^2{\mu_X}^2+b^2{\mu_Y}^2$인 정규분포를 따른다는 것을 알 수 있습니다. 이것으로 (b)에 대한 증명이 끝났습니다$\square$

10 다중변수 및 연합분포

이번 강의에서는 단일변수에 대한 분포가 아닌 다중변수에 대한 분포를 다룹니다. 단일변수에 대한 정의를 다시 떠올려보면, 원래 확률공간(probability space)이란, $(S,\Sigma,P)$이었습니다. $S$는 sample space로 그냥 하나의 집합이었고 $\Sigma$는 $\sigma$-algebra로서 $S$의 부분집합(사건)들의 집합 중에서 특정한 성질을 만족시키는 것들이었으며 $P:\Sigma\to[0,1]$는 probability measure로서 전사건에 대한 값이 1인 finite measure입니다. 그러니까, $P(A)$라고 할 때, $A$는 $S$의 부분집합, 즉 ‘사건’입니다. 그런데, 집합에 대한 함수를 다루기보다는 숫자에 대한 함수를 다루기 위해 확률변수라는 걸 도입하게 됩니다. 확률변수란, $X:S\to\mathbb R$인 함수 $x=X(w)$로 정의됩니다. 이를 통해

\[P(X=x)=P_X(x)\]

와 같은 표현을 ($P_X$는 확률질량함수, PMF)

\[P(X=x)=P\left(\{w\in S:X(w)=x\}\right)=P\left(X^{-1}(\{x\})\right)\]

로 정의하고

\[P(a\le X\le b)=\int_a^bf_X(x)\,dx\]

와 같은 표현을 ($f_X$는 확률밀도함수, PDF)

\[P(a\le X\le b)=P\left(\{w\in S:a\le X(w)\le b\}\right)=P\left(X^{-1}([a,b])\right)\]

로 정의하면 두 식 $P(X=x)$, $P(a\le X\le b)$은 잘 정의됩니다. 실제 강의에서는 $\sigma$-algebra라든지 probability measure에 대한 설명은 없이 진행됐습니다.

이번 강의에서는 두 확률변수 $X$, $Y$에 대하여

\[P(X=x, Y=y)\]

라든지

\[P(X\le x, Y\le y)\]

를 어떻게 정의할지 하는 문제를 다룹니다.

두 확률변수 $X:S_1\to\mathbb R$, $Y:S_2\to\mathbb R$를 고려한다고 해서 이 둘의 cartesian product를 확률변수로 놓을 수는 없습니다. $X\times Y:S_1\times S_2\to\mathbb R^2$을 $(X\times Y)(w_1,w_2)=(X(w_1),Y(w_2))$로 정의한다고 하면 이것은 공역이 $\mathbb R^2$이므로 확률변수라고 할 수 없기 때문입니다. 하지만, 순서쌍 $(X(w_1),Y(w_2))$에 대한 분포는 생각해볼 수 있습니다.

위에 언급한 값들을

\[\begin{align*} P(X=x,Y=y) &=P\left(\left\{(w_1,w_2)\in S_1\times S_2:X(w_1)=x,Y(w_2)=y\right\}\right)\\ &=P\left(X^{-1}(\{x\})\times Y^{-1}(\{y\})\right)\\ P(X\le x,Y\le y) &=P\left(\left\{(w_1,w_2)\in S_1\times S_2:X(w_1)\le x,Y(w_2)\le y\right\}\right)\\ &=P\left(X^{-1}(-\infty,x]\times Y^{-1}(-\infty,y]\right)\\ \end{align*}\]

로 정의하면 이것들은 잘 정의됩니다. 그러니까, $X^{-1}(\{x\})\times Y^{-1}(\{y\})\subset S_1\times S_2$이고, $X^{-1}(-\infty,x]\times Y^{-1}(-\infty,y]\subset S_1\times S_2$ 입니다. 사실은 각각의 집합들이 $S_1\times S_2$의 $\sigma$-algebra의 원소인지 하는 것도 봐야 더 정확하겠지만, 아래과 같은 언급에 따르면 $S_1\times S_2$에 대한 $\sigma$-algebra를 $\Sigma_1\times\Sigma_2$로 generate해서 만들어내면 문제가 되지 않는 것 같습니다;

The sigma-algebra on $E$ is generated by all products of the form $A_1\times\cdots\times A_n$, where $A_i$ is measurable in $E_i$ for each $i$.

이제 강의의 내용들을 따라서 써보겠습니다.

Chapter 5. Multiple Random Variables

5.2 joint CDF of bivarirate random variables

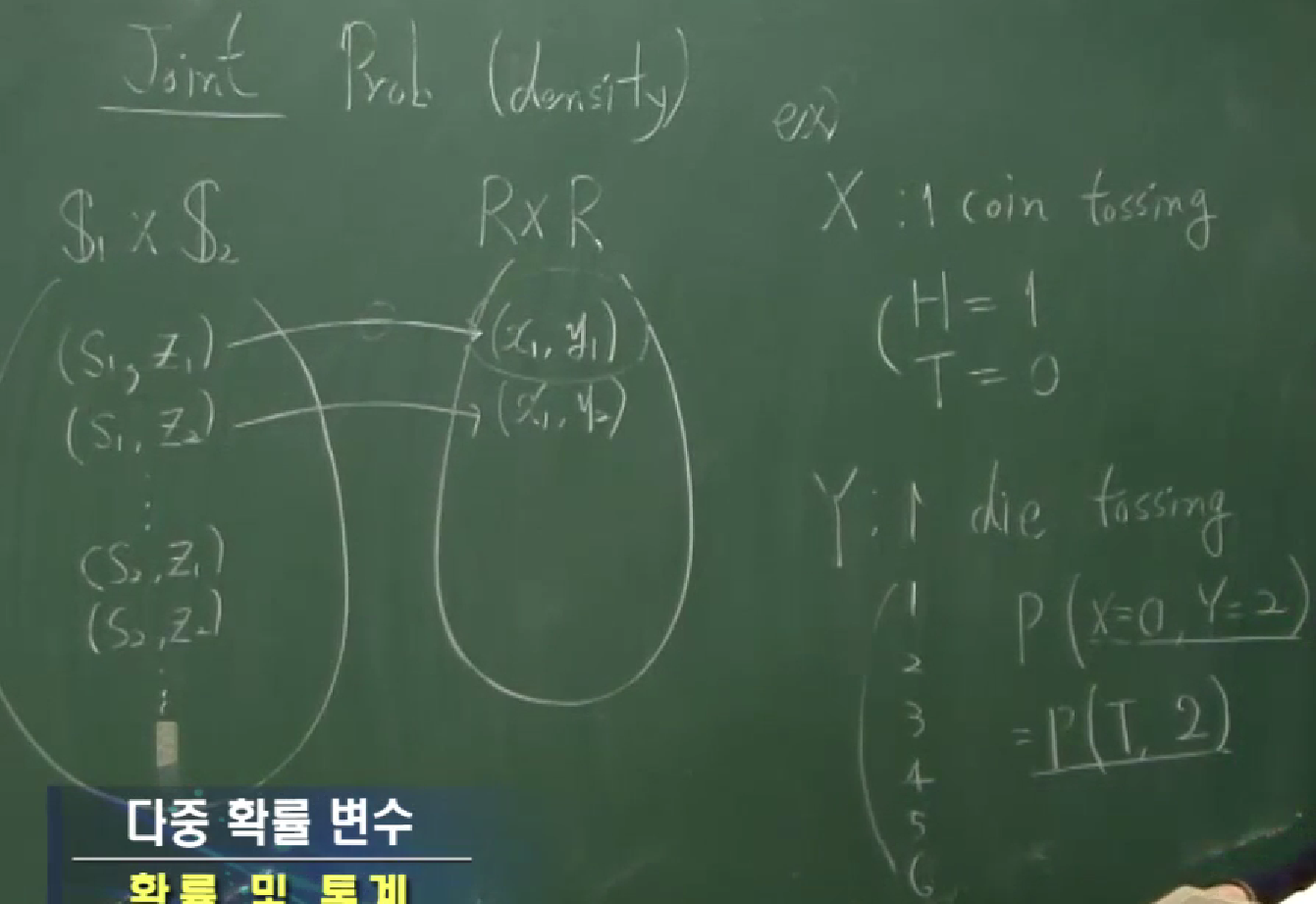
예를 들어. 동전과 주사위를 각각 하나씩 던져서 나오는 결과를 본다고 하면,

\[\begin{align*} X(H)&=1\\ X(T)&=0 \end{align*}\]

로 정의되는 확률변수 $X:\{H,T\}\to\mathbb R$와

\[\begin{align*} Y(1)&=1\\ Y(2)&=2\\ Y(3)&=3\\ Y(4)&=4\\ Y(5)&=5\\ Y(6)&=6 \end{align*}\]

로 정의되는 확률변수 $Y:\{1,2,3,4,5,6\}\to\mathbb R$를 생각하게 됩니다. 이때, $X$, $Y$의 joint PMF는

\[P(X=x,Y=y)=P\left(\{(w_1,w_2)\in S_1\times S_2:X(w_1)=x,Y(w_2)=y\}\right)\]

로 정의할 수 있습니다. (단, $S_1=\{H,T\}$, $S_2=\{1,2,3,4,5,6\}$) 예를 들어,

\[\begin{align*} P(X=0,Y=2) &=P\left(\{(w_1,w_2)\in S_1\times S_2:X(w_1)=0,Y(w_2)=2\}\right)\\ &=P\left(\{(T,2)\}\right)\\ &=\frac{n(\{(T,2)\})}{n(S_1\times S_2)}\\ &=\frac1{12} \end{align*}\]

입니다.

방금 계산한 것은 joint distribution에서의 PMF에 해당하는 것입니다. 그런데 $X$와 $Y$ 중 하나라도 연속확률변수이면 PMF를 정의하는 건 어려운 문제가 됩니다. 반면, CDF는 연속확률변수나 이산확률변수 모두에 대해 잘 정의됩니다. 그러니, joint PMF와 joint PDF를 정의하기 전에 joint CDF의 정의를 먼저 보겠습니다. joint CDF는

\[F_{XY}(x,y)=P(X\le x, Y\le y)\]

와 같이 정의됩니다. 그리고 다음 성질들을 만족시킵니다.

\[\begin{align*} (1)~ &0\le F_{XY}(x,y)\le 1\\ (2)~ &F_{XY}(x_1,y_1)\le F_{XY}(x_1,y_2)\qquad(x_1\lt x_2,\:\:y_1\lt y_2)\\ &F_{XY}(x_1,y_1)\le F_{XY}(x_2,y_1)\\ (3)~ &\lim_{\substack{x\to\infty \\y\to\infty}}F_{XY}(x,y)=1\\ (4)~ &\lim_{x\to-\infty}F_{XY}(x,y)=0\\ &\lim_{y\to-\infty}F_{XY}(x,y)=0\\ (5)~ &P(x_1\lt X\le x_2,Y\le y)=F_{XY}(x_2,y)-F_{XY}(x_1,y)\\ (6)~ &P(x_1\lt X\le x_2,y_1\lt Y\le y_2) =F_{XY}(x_2,y_2)-F_{XY}(x_1,y_2)-F_{XY}(x_2,y_1)+F_{XY}(x_1,y_1)\\ \end{align*}\]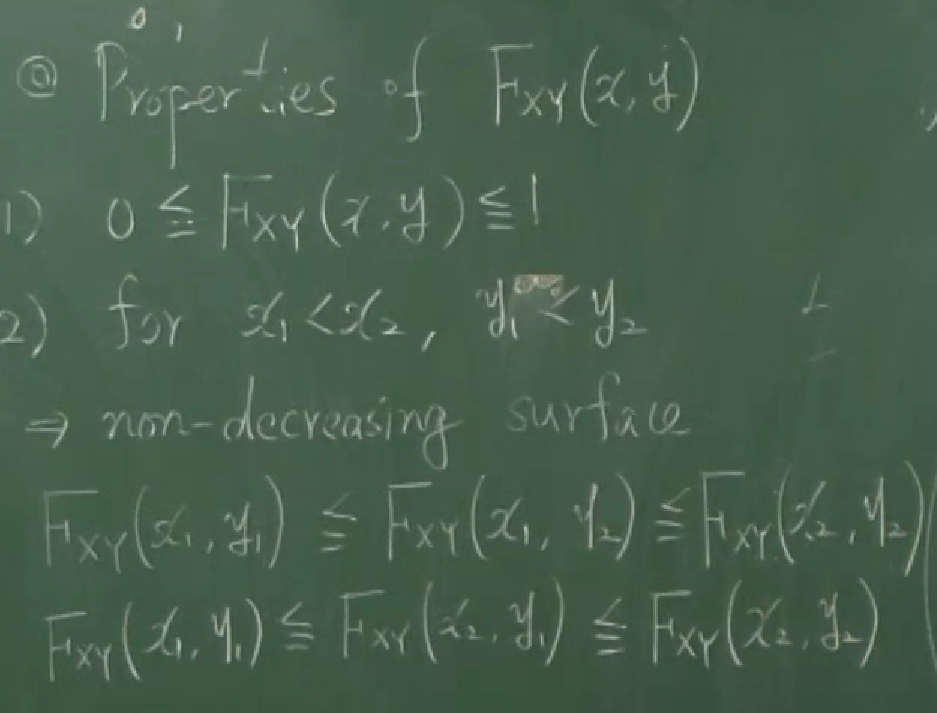

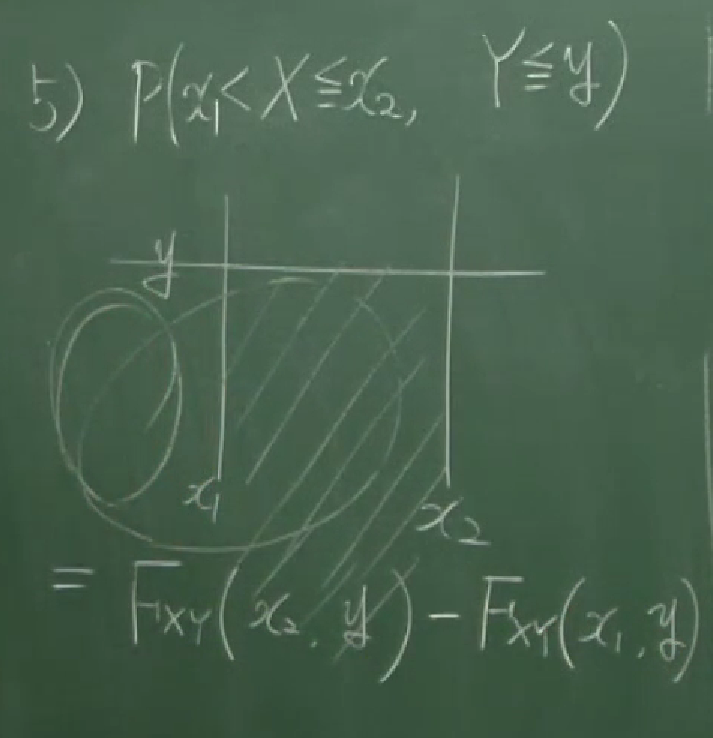
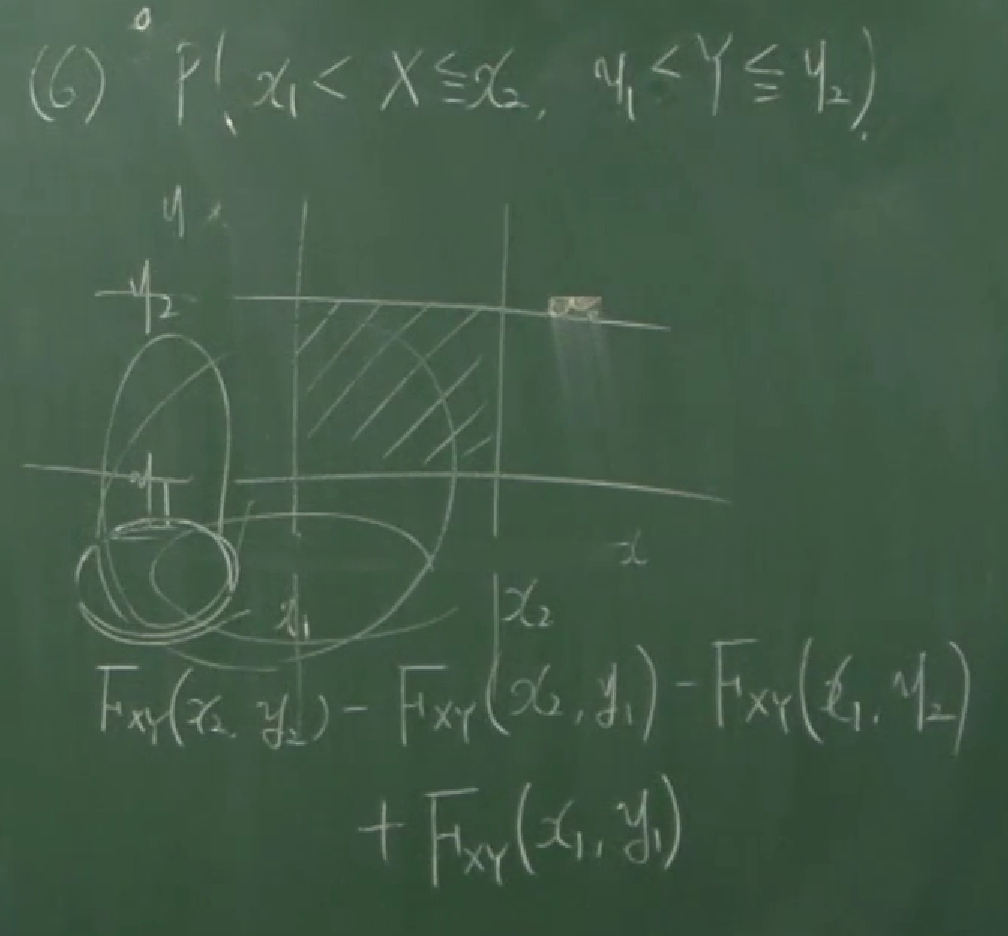
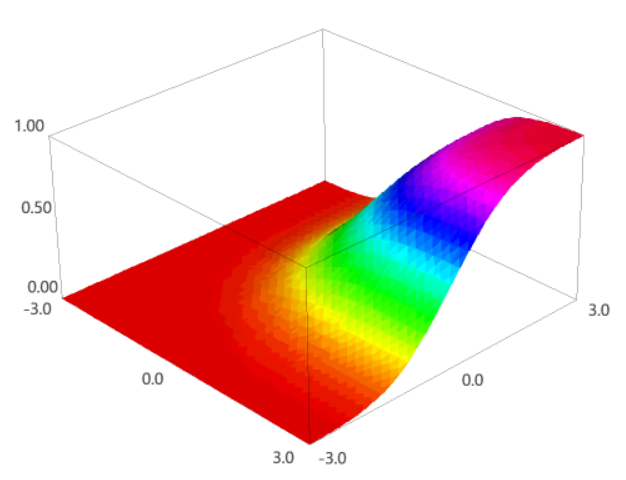
ex. 5.1

\[\begin{align*} P(X\gt x,Y\gt y) &=1-P(X\le x\text{ or }Y\le y)\\ &=1-\left(P(X\le x)+P(Y\le y)-P(X\le x, Y\le y)\right)\\ &=1-P(X\le x)-P(Y\le y)+P(X\le x, Y\le y)\\ &=1-F_X(x)-F_Y(y)+F_{XY}(x,y)\\ \end{align*}\]

위 계산에서 한 변수에 대해서의 CDF인 $F_X(x)$가 등장했습니다. 이와 같이, 두 변수에 대한 확률분포에서 특별히 한 변수에 대한 분포를 생각할때, 그 분포를 marginal distribution이라고 합니다. 이때, marginal CDF와 joint CDF 사이에는 다음과 같은 관계가 성립합니다.

\[\begin{align*} F_X(a)&=\lim_{y\to\infty}F_{XY}(a,y)\\ F_Y(b)&=\lim_{x\to\infty}F_{XY}(x,b) \end{align*}\]

5.3 discrete joint distributions

이산확률변수 $X$, $Y$에 대하여 $X$와 $Y$의 joint distribution에 대한 PMF는

\[P_{XY}(x,y)=P(X=x,Y=y)\]

로 정의됩니다. joint PMF는 다음 성질들을 만족시킵니다.

\[\begin{align*} (1)~ &0\le P_{XY}(x,y)\le1\\ (2)~ &\sum_x\sum_y P_{XY}(x,y)=1\\ (3)~ &F_{XY}(x,y)=P(X\le x,Y\le y)=\sum_{\tilde x\le x}\sum_{\tilde y\le y}P_{XY}(\tilde x,\tilde y)\\ (4)~ &P_X(x)=\sum_y P_{XY}(x,y)\qquad(\text{marginalization})\\ &P_Y(y)=\sum_x P_{XY}(x,y)\\ (5)~ &P_{XY}(x,y)=P_X(x)P_Y(y)\qquad(X,Y:\text{independent}) \end{align*}\]

위의 성질 (1)-(4)는 모두 당연해 보이므로 따로 증명하지 않겠습니다. 그리고 (5)는 두 확률변수가 독립인 것의 정의입니다.

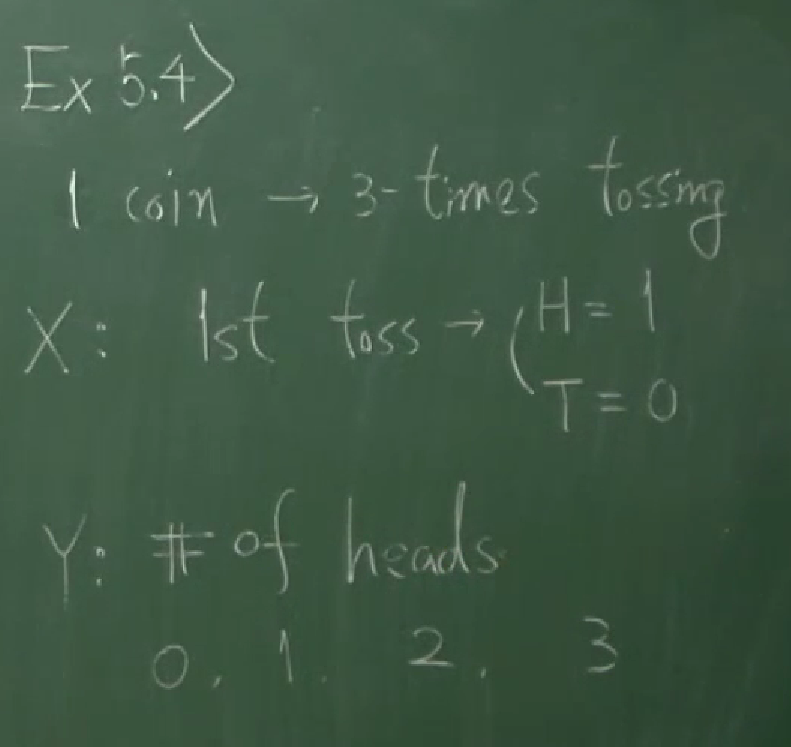
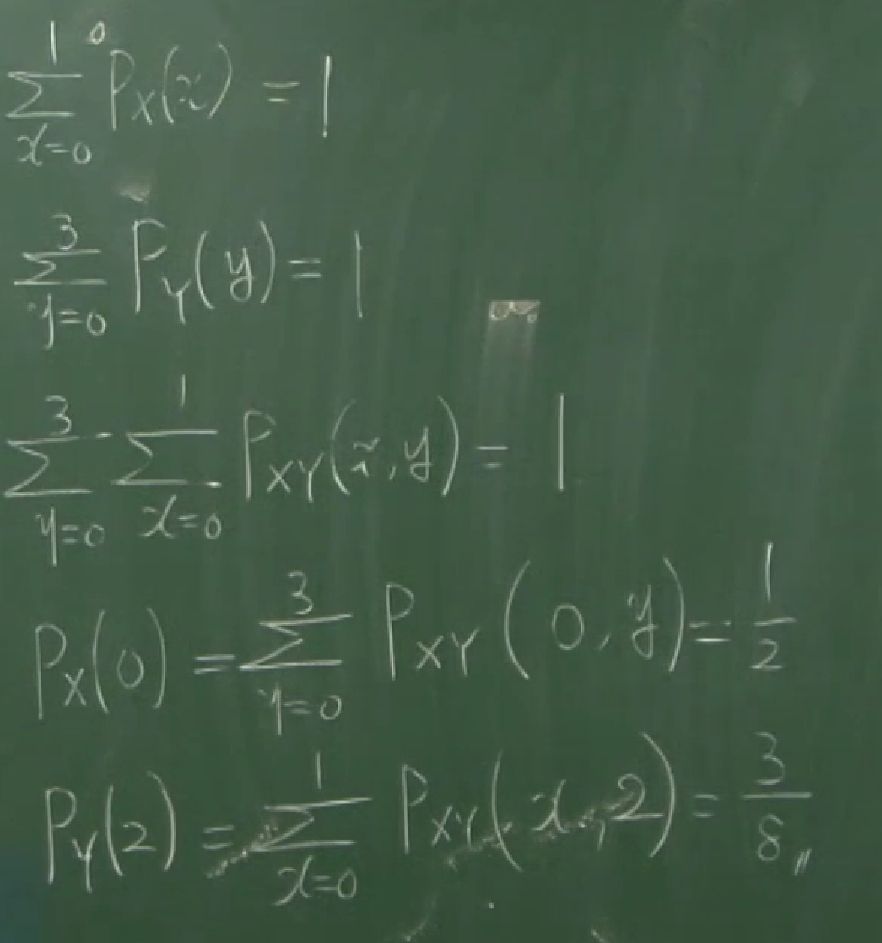
5.4 continuous joint distributions

연속확률변수 $X$의 PDF는 CDF의 도함수로서 정의했었습니다. $X$의 conditional PDF도 conditional CDF의 도함수로서 정의했습니다. 마찬가지로, 두 연속확률변수 $X$, $Y$에 대하여 $X$와 $Y$의 joint PDF를 정의하기 위해서는 일단 joint CDF를 먼저 정의해야 합니다. joint CDF는

\[F_{XY}(x,y)=P(X\le x,Y\le y)\]

와 같이 정의됩니다. 연속확률변수 $X$에 대하여 $P(X=x)$의 값을 정하는 것의 의미가 없었습니다. 변수가 두 개일 때에도 $P(X=x,Y=y)$는 0으로 정할 수밖에 없고, 그건 큰 의미가 있지 않습니다. 그래서 joint PDF $f_{XY}(x,y)$를

\[\begin{align*} f_{XY}(x,y) &=\lim_{\substack{\Delta x\to0+\\\Delta y\to0+}}\frac{P\left(x<X\le x+\Delta x,y<X\le y+\Delta y\right)}{\Delta x\Delta y}\\ &=\lim_{\substack{\Delta x\to0+\\\Delta y\to0+}} \frac{F_{XY}(x+\Delta x,y+\Delta y)-F_{XY}(x+\Delta x,y)-F_{XY}(x,y+\Delta y)+F_{XY}(x,y)}{\Delta x\Delta y}\\ &=\lim_{\Delta x\to0+}\frac1{\Delta x}\lim_{\Delta y\to0+} \frac{F_{XY}(x+\Delta x,y+\Delta y)-F_{XY}(x+\Delta x,y)-F_{XY}(x,y+\Delta y)+F_{XY}(x,y)}{\Delta y}\\ &=\lim_{\Delta x\to0+}\frac1{\Delta x}\left( \lim_{\Delta y\to0+}\frac{F_{XY}(x+\Delta x,y+\Delta y)-F_{XY}(x+\Delta x,y)}{\Delta y}- \lim_{\Delta y\to0+}\frac{F_{XY}(x,y+\Delta y)-F_{XY}(x,y)}{\Delta y} \right)\\ &=\lim_{\Delta x\to0+}\frac1{\Delta x}\left( \frac{F_{XY}}{\partial y}(x+\Delta x,y) -\frac{F_{XY}}{\partial y}(x,y)\right)\\ &=\frac{\partial}{\partial x}\frac{\partial}{\partial y}F_{XY}(x,y)\\ &=\frac{\partial^2}{\partial x\partial y}F_{XY}(x,y) \end{align*}\]

로 정의합니다. 이 함수는 $F_{XY}$가 충분히 좋은 함수이면 (e.g. 연속함수) 잘 정의됩니다.

joint PDF는 다음 성질들을 만족시킵니다.

\[\begin{align*} (1)~ &f_{XY}(x,y)\ge0\\ (2)~ &\iint_{\mathbb R^2}f_{XY}(x,y)\,dx\,dy=1 =\lim_{\substack{x\to\infty\\y\to\infty}}F_{XY}(x,y)\\ (3)~ &\int_{y_1}^{y_2}\int_{x_1}^{x_2}f_{XY}(x,y)\,dx\,dy=P\left(x_1\lt X\le x_2,~~y_1\lt Y\le y_2\right)\\ &=F_{XY}(x_2,y_2)-F_{XY}(x_1,y_2)-F_{XY}(x_2,y_1)+F_{XY}(x_1,y_1)\\ (4)~ &f_X(x)=\int_{-\infty}^\infty f_{XY}(x,y)\,dy\qquad(\text{marginalization})\\ &f_Y(y)=\int_{-\infty}^\infty f_{XY}(x,y)\,dx\\ (5)~ &f_{XY}(x,y)=f_X(x)f_Y(y)\qquad(X,Y:\text{independent}) \end{align*}\]

이때, $\iint_{\mathbb R^2}=\int_{-\infty}^\infty\int_{-\infty}^\infty$ 입니다. 이번에도 (1)-(4)는 당연합니다. 그리고 (5)는 두 확률변수가 독립인 것의 정의입니다.

11 연합확률밀도함수와 조건부확률밀도함수

ex. 5.6

두 확률변수에 대하여 joint PDF가

\[f_{XY}(x,y)=2e^{-x-y}\qquad(0\le x\le y,\quad 0\le y)\]

로 주어지는 경우에 대하여 앞서 강의에서의 성질들이 성립하는지 살펴보겠습니다. 이 함수가 정의된 영역을 $D$로 두면

\[D=\{(x,y)\in\mathbb R^2:0\le x\le y, 0\le y\}\]

이고 이것은

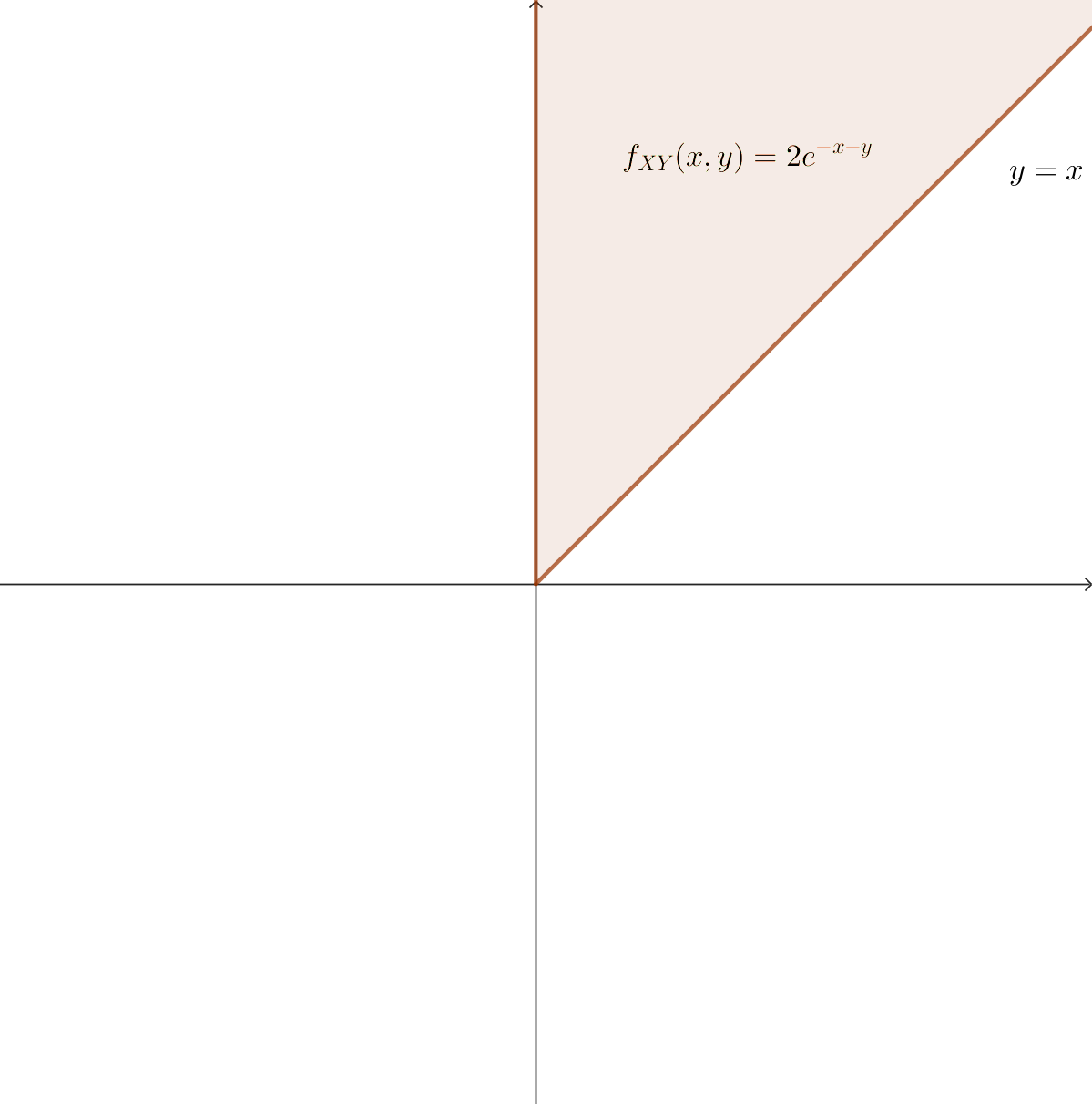
와 같은 영역을 의미합니다. 먼저 (2)번 성질($\iint_{\mathbb R^2} f_{XY}(x,y)\,dx\,dy=1$)을 보겠습니다. 이중적분의 순서에 따라 다음의 두 가지 방법으로 계산될 수 있습니다.

\[\begin{align*} \iint_{\mathbb R^2}f_{XY}(x,y)\,dx\,dy &=\iint_D f_{XY}(x,y)\,dx\,dy\\ &\stackrel{(a)}=\int_0^\infty\int_0^yf_{XY}(x,y)\,dx\,dy\\ &=\int_0^\infty\int_0^y2e^{-x-y}\,dx\,dy\\ &=\int_0^\infty\left[-2e^{-x-y}\right]_{x=0}^{x=y}\,dy\\ &=\int_0^\infty2e^{-y}-2e^{-2y}\,dy\\ &=\left[e^{-2y}-2e^{-y}\right]_0^\infty\\ &=0-(1-2)\\ &=1\\ \iint_{\mathbb R^2}f_{XY}(x,y)\,dx\,dy &=\iint_D f_{XY}(x,y)\,dx\,dy\\ &\stackrel{(b)}=\int_0^\infty\int_x^\infty f_{XY}(x,y)\,dy\,dx\\ &=\int_0^\infty\int_x^\infty2e^{-x-y}\,dy\,dx\\ &=\int_0^\infty\left[-2e^{-x-y}\right]_{y=x}^{y=\infty}\,dx\\ &=\int_0^\infty2e^{-2x}\,dx\\ &=\left[-e^{-2x}\right]_0^\infty\\ &=1 \end{align*}\]

이때,

\[\begin{align*} f_X(x) &=\int_x^\infty f_{XY}(x,y)\,dy\\ f_Y(x) &=\int_0^y f_{XY}(x,y)\,dx\\ \end{align*}\]

이므로, marginal PDF인 $f_X(x)$와 $f_Y(y)$는 (b)와 (a)의 계산 과정에서 구해진 셈입니다(4). 다시 말해,

\[\begin{align*} f_X(x) &=2e^{-y}-2e^{-2y}\\ f_Y(x) &=2e^{-2x}\\ \end{align*}\]

입니다. 따라서

\[f_{X,Y}(x,y)\ne f_X(x)f_Y(y)\]

이고, $X$와 $Y$는 독립이 아닙니다(5).

ex. 5.7

다음으로

\[f_{XY}(x,y)=\frac1{\pi r^2}\qquad(x^2+y^2\le1)\]

와 같이 joint PDF가 주어지는 경우입니다. 다시 말해, 단위원 내부에서 분포가 uniform distribution으로 주어지는 경우입니다. 이 함수가 정의된 영역은

\[D=\{(x,y)\in\mathbb R^2:x^2+y^2\le1\}\]

이고 이것은

와 같은 영역을 의미합니다. 이번에는 (2)번 성질이 당연합니다;

\[\begin{align*} \iint_{\mathbb R^2}f_{XY}(x,y)\,dx\,dy &=\iint_D f_{XY}(x,y)\,dx\,dy\\ &=\iint_D\frac1{\pi r^2}\,dx\,dy\\ &=\frac1{\pi r^2}\iint_D\,dx\,dy\\ &=\frac1{\pi r^2}\times\pi r^2\\ &=1 \end{align*}\]

이 계산은, 아까처럼 $dx\,dy$ 혹은 $dy\,dx$로 해도 잘 풀립니다. 또한 $r\,dr\,d\theta$로 풀어도 잘 계산됩니다. marginal PDF를 계산해보면

\[\begin{align*} f_X(x) &=\int_{-\sqrt{r^2-x^2}}^{\sqrt{r^2-x^2}}f_{XY}(x,y)\,dy\\ &=\int_{-\sqrt{r^2-x^2}}^{\sqrt{r^2-x^2}}\frac1{\pi r^2}\,dy\\ &=\frac{2\sqrt{r^2-x^2}}{\pi r^2} \end{align*}\]

이고, 마찬가지로

\[f_Y(y)=\frac{2\sqrt{r^2-y^2}}{\pi r^2}\]

입니다(4). 따라서

\[f_{X,Y}(x,y)\ne f_X(x)f_Y(y)\]

이고, 이번에도 $X$와 $Y$는 독립이 아닙니다(5).

5.6 conditional distribution

다음 개념인 conditional distribution으로 넘어가기 전에, 지금까지 학습한 개념들을 정리해보겠습니다.

\[\begin{matrix} \text{CDF(03)}&\text{PMF(03)}&\text{PDF(04)}&\text{exp.}(05)&\text{var.}(05)\\ \text{con. CDF(06)}&\text{con. PMF(06)}&\text{con. PDF(06)}&\text{con. exp.}(06)\\ \text{jnt. CDF(10)}&\text{jnt. PMF(10)}&\text{jnt. PDF(10)}\\ \end{matrix}\]

여기에서 괄호 안의 숫자는 강의의 회차를 의미하고, exp.는 expectation, var.은 variance, con.은 conditional, jnt.는 joint를 의미합니다.

그러니까 conditional variance에 대해서는 다루지 않았는데, 이번 강의에서 언급됩니다. 한편 joint expectation과 joint variance의 개념은 생각할 수 없습니다. joint distribution에 대해서는 어떤 실수값을 가지는 확률변수를 생각할 수 없었기 때문입니다. 하지만, 여러 개의 확률변수들에 특정한 함수가 주어졌을 때의 expectation은 계산할 수 있습니다$\langle12\rangle$. 또 joint variance를 정의하는 대신 covariance를 정의하게 됩니다$\langle12\rangle$.

이번 강의에서 공부하는 것은 conditional distribution이지만, $\langle06\rangle$에서 다루었던 일반적인 conditional distribution말고, 두 확률변수에 대해 생각할 때의 conditional distribution을 공부합니다.

\[\begin{matrix} \text{con2. CDF(11)}&\text{con2. PMF(11)}&\text{con2. PDF(11)}&\text{con2. exp.(11)}&\text{con2. var.(11)} \end{matrix}\]

이전 강의들에서

\[\begin{align*} P(A|B) &=\frac{P(A\cap B)}{P(B)} &&\text{(conditional probability w.r.t. events(01))}\\ P(X\le x|X\le a) &=\frac{P\left((X\le x)\cap(X\le a)\right)}{P(X\le a)} &&\text{(conditional probability w.r.t. RVs(06))} \end{align*}\]

와 같은 것들을 공부했습니다.

두 이산확률변수 $X$와 $Y$에 대하여 조건부 확률질량함수(conditional PMF)에 해당하는 함수 $P_{Y\vert X}$를

\[\begin{align*} P_{Y|X}(y|x) &=P(Y=y|X=x)\\ &=\frac{P_{XY}(x,y)}{P_X(x)} \end{align*}\]

와 같이 정의합니다.

(설명을 자세히 적지 않고 캡쳐로 대체했지만) 이전 강의 $\langle 10\rangle$에서 나왔던 예를 다시 살펴보겠습니다. 동전을 세 개 던질 때, $X$를

첫번째 동전이 앞면이면 1, 뒷면이면 0

으로 정하고 $Y$를

세 동전 중 앞면의 개수

로 정할 때 $X$, $Y$의 joint distribution이

와 같이 나옴을 확인했었습니다.

이때,

\[P_{Y|X}(1|0)=\frac{P_{XY}(0,1)}{P_X(0)}=\frac{\frac28}{\frac18+\frac28+\frac18}=\frac12\]

입니다.

이번에는 $X$, $Y$가 연속확률변수인 경우를 살펴봅니다. 이전과 마찬가지로 CDF에서부터 출발합니다. 이때, conditional CDF는

\[F_{Y|X}(y|x)=P(Y\le y|X=x)\]

의 의미입니다. ($X$가 $x$로 주어져 있을 때, $Y$의 CDF입니다.) 그런데

\[F_{Y|X}(y|x)=\frac{P(X=x,Y\le y)}{P(X=x)}\]

와 같이 정의할 수는 없습니다. 왜냐하면 분모가 0이 될 가능성이 있기 때문입니다. 그러니까, 지금까지 CDF, (일반적인) conditional CDF, joint CDF가 별 문제 없이 정의되었던 것과는 조금 다릅니다. 위와 같은 정의 대신에, $y$를 포함하는 infinitesimal한 구간 $x\lt X\le x+\Delta x$를 고려하여

\[F_{Y|X}(y|x)\approx\frac{P(x\lt X\le x+\Delta x,Y\le y)}{P(x\lt X\le x+\Delta x)}\]

와 같이 생각할 수 있습니다. 그리고 우변에 $\Delta x\to0+$인 극한을 취해주어, 그 극한값을 $F_{Y|X}(y|x)$로 정해주는 것이 합리적입니다. 그러면

\[\begin{align*} F_{Y|X}(y|x) &=\lim_{\Delta x\to0+}\frac{P(x\lt X\le x+\Delta x,Y\le y)}{P(x\lt X\le x+\Delta x)}\\ &=\lim_{\Delta x\to0+}\frac{P(x+\Delta x,Y\le y)-P(x,Y\le y)}{P(X\le x+\Delta x)-P(X\le x)}\\ &=\lim_{\Delta x\to0+}\frac{F_{XY}(x+\Delta x,y)-F_{XY}(x,y)}{F_X(x+\Delta x)-F_X(x)}\\ &=\frac{\displaystyle\lim_{\Delta x\to0+}\frac{F_{XY}(x+\Delta x,y)-F_{XY}(x,y)}{\Delta x}}{\displaystyle\lim_{\Delta x\to0+}\frac{F_X(x+\Delta x)-F_X(x)}{\Delta x}}\\ &=\frac{\frac\partial{\partial x}F_{XY}(x,y)}{\frac\partial{\partial x}F_{X}(x)}\\ &=\frac{\frac\partial{\partial x}F_{XY}(x,y)}{f_{X}(x)} \end{align*}\]

입니다. 이제, conditional PDF를 정의할 수 있습니다. 이것은 conditional PDF를 $y$에 대해 편미분함으로써 얻어집니다;

\[\begin{align*} f_{Y|X}(y|x) &=\frac\partial{\partial y}F_{Y|X}(y|x)\\ &=\frac\partial{\partial y}\left(\frac{\frac\partial{\partial x}F_{XY}(x,y)}{f_{X}(x)}\right)\\ &=\frac1{f_{X}(x)}\frac\partial{\partial y}\left(\frac\partial{\partial x}F_{XY}(x,y)\right)\\ &=\frac{\frac{\partial^2}{\partial y\partial x}F_{XY}(x,y)}{f_{X}(x)}\\ &=\frac{f_{XY}(x,y)}{f_X(x)} \end{align*}\]

마찬가지로 $X$와 $Y$의 위치를 바꾸면

\[f_{X|Y}(x|y)=\frac{f_{XY}(x,y)}{f_Y(y)}\]

입니다.

conditional expectations and variances

$\langle06\rangle$에서 (일반적인) conditional expectation은 (continuous case)

\[E[X|X\le a]=\int_{x\le a}xf_X(x|X\le a)\,dx\]

와 같이 정의했었습니다. 예를 들어, 아래 그림과 같은 분포에서 $X\le a$라는 조건이 주어지면, 그렇지 않았을 때보다 평균이 왼쪽으로 이동하게 될 것입니다.

이번에 다루는 것은 (그러니까, 일반적인 conditional expectation이 아니라는 말은) $E[Y\vert A]$에서 $A$가 $X$에 대한 조건인 경우입니다 ; $E[Y\vert A_X]$ 다시 말해, $\langle06\rangle$에서는 $X$에 대한 조건 하에 $X$의 평균을 계산했다면, 이번에는 $X$에 대한 조건 하에 $Y$의 평균을 계산합니다. 자세한 것은 다음 강의에서 이어집니다.

12 조건부 평균과 공분산

이번 강의에서 다루는 것은, 드디어 $E[Y|X]$ 입니다. 개인적으로는 이것의 정확한 의미를 파악하지 못해 고생한 적이 있습니다.

강의의 가장 초반부에 $E[Y|X]$의 의미는 사실은 $E[Y|X=x]$의 의미라는 언급이 있습니다. 사실 $E[Y|X]$는 그 자체로는 아직 정의된 적이 없는 어떤 개념입니다. conditional expectation에서 condition에 어떤 ‘확률변수’가 들어가있습니다. 지금까지 condition에 들어갈 수 있었던 것은 $S$의 부분집합(사건) 혹은 확률변수가 포함된 조건(e.g. $X=x$, $X\le x$)이었지 확률변수 그 자체는 아니었던 것입니다. 하지만, $E[Y|X=x]$라고 하면 의미가 생깁니다. 이것은 $X=x$인 조건 하에서의 $Y$의 기댓값을 의미합니다.

더 나아가 이해해야 할 것은 $E[Y|X]$가 확률변수라는 사실입니다. $E[Y|X=x]$는 $Y$의 기댓값이기 때문에 $Y$라든지 $y$라든지 하는 값에 의존하지 않습니다. 이것은 오로지 $x$에 의존하는 값입니다. 다시 말해, $x$에 대한 함수입니다;

\[E[Y|X=x]=g(x)\]

그러면 $E[Y\vert X]$를

\[E[Y|X]=g(X)\]

로 정의하면 이 값은 하나의 확률변수로 생각할 수 있는 것입니다. 예를 들어, $X$가 확률변수이면 $X$에 대한 함수 $X^2$도 확률변수인 것처럼, $X$가 확률변수이기 때문에 $g(X)$도 확률변수인 것입니다. 더 깊이 말하면, $X$와 $Y$가 각각 $X:S_1\to\mathbb R$이고 $Y:S_2\to\mathbb R$인 확률변수들이라고 할 때, 새로운 확률변수

\[E[Y|X]:S_1\to\mathbb R\]

을

\[E[Y|X](w)=E[Y|X=X(w)]\]

로 정의하면 이것은 잘 정의된 확률변수이고, 위에서 말한 의미와도 부합합니다.

사실, 강의에서는 $E[Y\vert X]$의 의미에 대해서는 설명하지 않는 것으로 보이고, 조금은 notation abusing을 하는 것으로 보입니다.

이제 강의를 따라서 $E[Y|X=x]$의 정의를 적어보겠습니다. 아래 식에서 첫번째 등호가 정의이고, 두번째 등호는 conditional PMF의 성질을 사용한 것입니다.

\[\begin{align*} E[Y|x=x] &=\int_\mathbb Ryf_{Y|X}(x,y)\,dy\\ &=\int_\mathbb Ry\frac{f_{XY}(x,y)}{f_X(x)}\,dy \end{align*}\]

둘째 줄의 적분을 계산할 때 $y$가 사라지므로, 적분값을 $x$에 대한 함수로서 놓을 수 있습니다. 따라서, 아까 언급한 것처럼 $E[Y\vert X=x]$는 $x$에 대한 함수입니다.

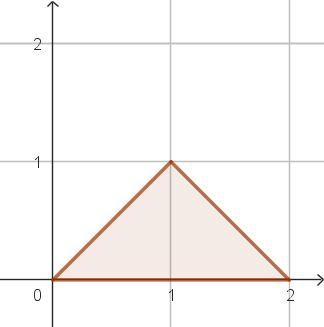
위의 그림은, 강의의 예시를 구체화해서 적어본 것입니다. 좌표평면 위에 $(0,0)$, $(2,0)$, $(1,1)$을 꼭짓점으로 하는 삼각형의 내부에 점 $P$가 위치한다고 할 때, $P$의 $x$좌표와 $y$좌표를 각각 $X$, $Y$라고 하겠습니다. $P$가 삼각형 내부에 균일한 정도의 가능성으로 존재할 때 (uniform distribution) $X$, $Y$의 joint PDF는

\[f_{XY}(x,y)=1\qquad(0\le y\le x, y\le 2-x)\]

입니다. 이때, $E[X|Y=y]$와 $E[Y|X=x]$를 계산해보려 합니다. 계산을 하기 전에 직관적으로 살펴보면, $y$의 값이 어떤 값이건 상관없이 $(0\lt y\lt 1)$ $X$가 위치하는 구간은 $1$을 중심으로 하는 구간입니다. 또한, $X$가 여전히 uniform distribution을 따를 것이므로, $X$의 평균은 1일 수밖에 없습니다. 따라서 $E[X|Y=y]=1$입니다. 반대로 $x$ 값이 고정되어 있다고 생각하겠습니다. 이번에는 $x$가 $0\le x\le1$인 경우와 $1\le x\le2$인 경우의 상황이 다릅니다. $0\le x\le1$이면, $Y$는 $0$부터 $x$ 사이를 움직이고, 따라서 그 평균은 $\frac12x$가 될 것입니다. $1\le x\le2$이면, $Y$는 $0$부터 $2-x$ 사이를 움직이고, 따라서 그 평균은 $\frac12(2-x)$가 될 것입니다.

계산해보면

\[\begin{align*} E[X|Y=y] &=\int_y^{2-y}xf_{X|Y}(x,y)\,dx\\ &=\int_y^{2-y}x\frac{f_{XY}(x,y)}{f_Y(y)}\,dx\\ &=\int_y^{2-y}x\frac{f_{XY}(x,y)}{\int_y^{2-y}f_{XY}(x,y)\,dx}\,dx\\ &=\int_y^{2-y}x\frac1{\int_y^{2-y}\,dx}\,dx\\ &=\int_y^{2-y}x\frac1{2-2y}\,dx\\ &=\frac1{2-2y}\int_y^{2-y}x\,dx\\ &=\frac1{2-2y}\times\frac12\left((2-y)^2-y^2\right)\\ &=1 \end{align*}\]

이고

$0\le x\le 1$일 때의 $E[Y\vert X=x]$는

\[\begin{align*} E[Y|X=x] &=\int_0^xyf_{Y|X}(x,y)\,dy\\ &=\int_0^xy\frac{f_{XY}(x,y)}{f_X(x)}\,dy\\ &=\int_0^xy\frac{f_{XY}(x,y)}{\int_0^xf_{XY}(x,y)\,dy}\,dy\\ &=\int_0^xy\frac1{\int_0^x\,dy}\,dy\\ &=\int_0^xy\frac1x\,dy\\ &=\frac1x\int_0^xy\,dy\\ &=\frac12x \end{align*}\]

이고, $1\le x\le 2$일 때의 $E[Y\vert X=x]$는

\[\begin{align*} E[Y|X=x] &=\int_0^{2-x}yf_{Y|X}(x,y)\,dy\\ &=\int_0^{2-x}y\frac{f_{XY}(x,y)}{f_X(x)}\,dy\\ &=\int_0^{2-x}y\frac{f_{XY}(x,y)}{\int_0^{2-x}f_{XY}(x,y)\,dy}\,dy\\ &=\int_0^{2-x}y\frac1{\int_0^{2-x}\,dy}\,dy\\ &=\int_0^{2-x}y\frac1{2-x}\,dy\\ &=\frac1{2-x}\int_0^{2-x}y\,dy\\ &=\frac12(2-x) \end{align*}\]

입니다.

ex.5.10

두 연속확률변수 $X$, $Y$에 대한 PDF가 다음과 같이 주어졌다고 가정하겠습니다.

\[f_{XY}(x,y)=\frac1ye^{-\frac xy}e^{-y}\qquad(x\gt0, y\gt0)\]

정말로 PDF가 맞는지 (예의상) 계산해보면

\[\begin{align*} \int_0^\infty\int_0^\infty f_{XY}(x,y)\,dx\,dy &=\int_0^\infty\frac{e^{-y}}y\int_0^\infty e^{-\frac xy}\,dx\,dy\\ &=\int_0^\infty\frac{e^{-y}}y\left[-ye^{-\frac xy}\right]_{x=0}^{x=\infty}\,dy\\ &=\int_0^\infty e^{-y}\,dy\\ &=1 \end{align*}\]

입니다. conditional expectation $E[X|Y=y]$을 계산하기 전에, 그 과정에 쓰이는 $f_Y(y)$를 먼저 계산해보면

\[\begin{align*} f_Y(y) &=\int_0^\infty f_{XY}(x,y)\,dx\\ &=\int_0^\infty\frac1ye^{-\frac xy}e^{-y}\,dx\\ &=\frac{e^{-y}}y\left[-ye^{-\frac xy}\right]_{x=0}^{x=\infty}\\ &=e^{-y} \end{align*}\]

입니다. 이제 계산을 해보면

\[\begin{align*} E[X|Y=y] &=\int_0^\infty xf_{X|Y}(x,y)\,dx\\ &=\int_0^\infty x\frac{f_{XY}(x,y)}{f_Y(y)}\,dx\\ &=\int_0^\infty x\times\frac{\frac1ye^{-\frac xy}e^{-y}}{e^{-y}}\,dx\\ &=\int_0^\infty\left(\frac xy\right)e^{-\frac xy}\,dx\\ &=y\int_0^\infty\left(\frac xy\right)e^{-\frac xy}\,d\left(\frac xy\right)\\ &=y\left[te^{-t}-e^{-t}\right]_{t=0}^{t=\infty}\\ &=y \end{align*}\]

입니다. 중간 계산과정에서 $\int te^{-t}\,dt=-te^{-t}-e^{-t}+C$를 활용했습니다.

이번에는, 확률변수 $X$에 대하여 $g(X)$의 확률을 구하는 식이 강의에 소개됩니다. 이것은 $\langle05\rangle$에서 LOTUS(law of the unconscious statistician)라는 이름으로 언급한 적이 있는 식입니다;

\[\begin{align*} E[g(X)]&=\sum_ig(x_i)P_X(x_i) &&(\text{discrete})\\ E[g(X)]&=\int_{-\infty}^\infty g(x)f_X(x)\,dx &&(\text{continuous}) \end{align*}\tag{LOTUS}\]

이에 대한 증명은 $\langle14\rangle$에서 해봅니다. 마찬가지로, 다변수 함수 $g(X,Y)$에 대해서도

\[\begin{aligned} E\left[g(X,Y)\right]&=\int_{\mathbb R^2} g(x,y)f_{XY}(x,y)\,dx &&\text{(continuous)}\\ E\left[g(X,Y)\right]&=\sum_{i=1}^m\sum_{j=1}^ng(x_i,y_j)P_X(x_i,y_j) &&\text{(discrete)}\\ \end{aligned}\tag{$\ast$}\]

입니다. 또한, 두 확률변수 $X$, $Y$에 대하여, 두 함수 $g_1(X,Y)$, $g_2(X,Y)$가 존재할 때, 두 실수 $\alpha$, $\beta$에 대하여

\[E\left[\alpha g_1(X,Y)+\beta g_2(X,Y)\right] =\alpha E\left[g_1(X,Y)\right]+\beta E\left[g_2(X,Y)\right] \tag{$\ast\ast$}\]

입니다. 즉, $E$는 다변수 함수에 대해서도 linear operator입니다. 왜냐하면

\[\begin{align*} E\left[g_1(X,Y)+g_2(X,Y)\right] &=\iint_{\mathbb R^2}\left(g_1(X,Y)+g_2(X,Y)\right)f_{XY}(x,y)\,dx\,dy\\ &=\iint_{\mathbb R^2}\left(g_1(X,Y)\right)f_{XY}(x,y)\,dx\,dy +\iint_{\mathbb R^2}\left(g_2(X,Y)\right)f_{XY}(x,y)\,dx\,dy\\ &=E\left[g_1(X,Y)\right]+E\left[g_2(X,Y)\right] \end{align*}\]

이고,

\[\begin{align*} E\left[\alpha g(X,Y)\right] &=\iint_{\mathbb R^2}\alpha g(X,Y)f_{XY}(x,y)\,dx\,dy\\ &=\alpha\iint_{\mathbb R^2}g(X,Y)f_{XY}(x,y)\,dx\,dy\\ &=\alpha E\left[g(X,Y)\right] \end{align*}\]

이기 때문입니다.

이와 같은 사실들은 구구절절 다 소개되지는 않았지만, 암시적으로 언급되고 있는 것 같습니다.

ex.5.11 $E\left[E[X\vert Y]\right]=E[X]$

이번 성질을 이해하려면, 초반에 언급한

$E[X\vert Y]$는 확률변수이다.

라는 것을 확실히 알아야 합니다. 좌변에서 $E[X\vert Y]$에 대해 기댓값 연산을 취하고 있는데, 그럴 수 있는 것이 $E[X\vert Y]$가 그 자체로 확률변수이기 때문입니다. 앞서 언급한대로 $E[X\vert Y=y]$는 $y$의 함수입니다. $E[X\vert Y=y]$를

\[E[X|Y=y]=\int_{\mathbb R}xf_{X|Y}(x|y)\,dx=g(y)\]

로 쓰면 $E[X\vert Y]$를

\[E[X|Y]=g(Y)\]

와 같이 생각할 수 있다고 했습니다. 그런 관점에서 보면 $E\left[E[X\vert Y]\right]$는 $g(Y)$에 대한 평균을 의미합니다. 계산해보면

\[\begin{align*} E\left[E[X|Y]\right] &=E\left[g(Y)\right]\\ &=\int_{\mathbb R}g(y)f_Y(y)\,dy\\ &=\int_{\mathbb R}E[X|Y=y]f_Y(y)\,dy\\ &=\int_{\mathbb R}\left(\int_{\mathbb R}xf_{X|Y}(x|y)\,dx\right)f_Y(y)\,dy\\ &=\iint_{\mathbb R^2}xf_{X|Y}(x|y)f_Y(y)\,dx\,dy\\ &=\iint_{\mathbb R^2}xf_{XY}(x,y)\,dx\,dy\\ &=\int_{\mathbb R}x\int_{\mathbb R}f_{XY}(x,y)\,dy\,dx\\ &=\int_{\mathbb R}xf_X(x)\,dx\\ &=E[X] \end{align*}\]

입니다.

이것에 대한 discrete 버전의 증명은

\[\begin{align*} E\left[E[X|Y]\right] &=E\left[g(Y)\right]\\ &=\sum_{j=1}^ng(y_j)P_Y(y_j)\\ &=\sum_{j=1}^n\left(E[X|Y=y_i]\right)P_Y(y_j)\\ &=\sum_{j=1}^n\left(\sum_{i=1}^mx_iP_{X|Y}(x_i|y_i)\right)P_Y(y_j)\\ &=\sum_{j=1}^n\sum_{i=1}^mx_iP_{X|Y}(x_i|y_j)P_Y(y_j)\\ &=\sum_{j=1}^n\sum_{i=1}^mx_iP_{XY}(x_i,y_j)\\ &=\sum_{i=1}^mx_i\sum_{j=1}^nP_{XY}(x_i,y_j)\\ &=\sum_{i=1}^mx_iP_X(x_i)\\ &=E[X] \end{align*}\]

입니다. 여기에서 세번째 줄과 마지막 줄의 값을 같다고 두면

\[E[X]=\sum_{j=1}^n\left(E[X|Y=y_i]\right)P_Y(y_i)\]

인데, 이것은 law of total probability인

\[P(A)=\sum_{j=1}^nP(A|A_i)P(A_i)\]

와 구조가 거의 똑같다는 점이 강의에서 언급되고 있습니다.

5.7 covariance and correlation coefficient

covariance(공분산)

$X$와 $Y$가 확률변수이고, $E[X]=\mu_X$, $E[Y]=\mu_Y$이면, $X$와 $Y$ 사이의 공분산(covariance)을

\[\text{cov}(X,Y)=\sigma_{XY}=E\left[(X-\mu_X)(Y-\mu_Y)\right]\]

로 정의합니다. 물론, $(\ast)$에 의해

\[\begin{align*} \text{cov}(X,Y)&=\iint_{\mathbb R^2}(x-\mu_X)(y-\mu_Y)f_{XY}(x,y)\,dx\,dy&&(\text{continuous})\\ \text{cov}(X,Y)&=\sum_i\sum_j(x_i-\mu_X)(y_j-\mu_Y)P_{XY}(x,y)&&(\text{discrete}) \end{align*}\]

입니다. 또한, $(\ast\ast)$를 사용해 이것을 정리하면

\[\begin{aligned} \text{cov}(X,Y) &=E\left[XY-\mu_YX-\mu_XY+\mu_X\mu_Y)\right]\\ &\stackrel{\ast\ast}{=}E[XY]-\mu_YE[X]-\mu_XE[Y]+\mu_X\mu_Y\\ &=E[XY]-E[X]E[Y] \end{aligned} \tag{$\ast\ast\ast$}\]

입니다.

만약 $\text{cov}(X,Y)\ne0$이면, $X$와 $Y$는 상관성이 있다(correlated)고 말하고, $\text{cov}(X,Y)=0$이면, $X$와 $Y$는 상관성이 없다(uncorrelated)고 말합니다. 이때, 독립성은 uncorrelatedness를 보장합니다 ;

$X$, $Y$가 서로 독립이면, $X$와 $Y$는 상관성이 없습니다.

왜냐하면, $X$와 $Y$가 독립이라고 가정할 때,

\[\begin{align*} E[XY] &=\iint_{\mathbb R^2}xyf_{XY}(x,y)\,dx\,dy\\ &=\iint_{\mathbb R^2}xyf_X(x)P_Y(y)\,dx\,dy\\ &=\int_{\mathbb R}xf_X(x)\,dx\times\int_{\mathbb R}yf_Y(y)\,dy\\ &=E[X]E[Y] \end{align*}\]

가 되어 식 $(\ast\ast\ast)$의 우변이 0이 되기 때문입니다.

일반적으로, 두 확률변수 $X$, $Y$가 독립이면 $$E[g(X)h(Y)]=E[g(X)]E[h(Y)]$$ 입니다. 이에 대한 증명은 LOTUS로부터 당연합니다. \begin{align*} E[g(X)h(Y)] &\stackrel{\text{LOTUS}}= \int_{-\infty}^\infty\int_{-\infty}^\infty g(x)h(y)f_{XY}(x,y)\,dx\,dy\\ &=\int_{-\infty}^\infty\int_{-\infty}^\infty g(x)h(y)f_X(x)f_Y(y)\,dx\,dy\\ &=\int_{-\infty}^\infty g(x)f_X\,dx\times \int_{-\infty}^\infty h(y)f_Y(y)\,dy\\ &\stackrel{\text{LOTUS}}=E[g(X)]E[h(Y)] \end{align*}

하지만, uncorrelatedness가 독립성을 보장하지는 않습니다. 그 반례로, $X$가 $\{-1,0,1\}$의 uniform distribution이고 $Y=3X^2-2$이면, $X$와 $Y$는 uncorrelated하지만 독립조건이 깨집니다. $P_X(x)$는

\[\begin{align*} P_X(-1) &=\frac13\\[10pt] P_X(0) &=\frac13\\[10pt] P_X(1) &=\frac13 \end{align*}\]

이고 $E[X]=0$이며, $P_Y(y)$는

\[\begin{align*} P_Y(-2) &=\frac13\\[10pt] P_Y(1) &=\frac23 \end{align*}\]

이고, $E[Y]=0$입니다. 또, $P_{XY}(x,y)$는

\[\begin{matrix} &X=-1 &X=0 &X=1 \\[20pt] Y=-2 &P_{XY}=0 &P_{XY}=\frac13 &P_{XY}=0 \\[20pt] Y=1 &P_{XY}=\frac13 &P_{XY}=0 &P_{XY}=\frac13 \end{matrix}\]

이므로,

\[\begin{align*} E[(X-\mu_X)(Y-\mu_Y)] &=E[XY]\\ &=(-1)\times\frac13+0\times\frac13+1\times\frac13\\ &=0 \end{align*}\]

이라서 $X$와 $Y$는 uncorrelated합니다. 하지만,

\[\begin{align*} P(X=-1) &=\frac13\\ P(Y=-2) &=\frac13\\ P(X=-1,Y=-2)&=0 \end{align*}\]

이 되어 $P(X=-1)P(Y=-2)\ne P(X=-1,Y=-2)$이고, 따라서 $X$와 $Y$는 독립이 아닙니다.

이 반례는, correlated라는 뜻이 “두 확률변수가 연관되어있다”는 것이 아니라는 것도 알려줍니다. 실제로 위와 같은 $X$와 $Y$는 $Y=3X^2-2$와 같은 ‘연관성’이 분명히 있는데도 불구하고 uncorrelated인 것입니다.

다음 개념으로 넘어가기 전에, covariance의 여러 성질들을 적어보겠습니다. 가장 먼저 covarinace의 bilinearity입니다 : (a), (b). 다시 말해, 함수 $\text{cov}(\cdot,\cdot)$이 각 성분에 대하여 linear하다는 것입니다. 또한, 상수를 더하는 것(additive constant)이 covariance의 값에 영향을 주지 않는다는 것도 언급하겠습니다 : (c), (d). 마지막으로 covarinace가 symmetric한 성질을 가진다는 것도 언급해보려고 합니다 : (e). 구체적으로 말하면 다음과 같습니다.

(a) $\text{cov}(aX+bY,Z)=a\text{cov}(X,Z)+b\text{cov}(X,Z)$
(b) $\text{cov}(X,aY+bZ)=a\text{cov}(X,Y)+b\text{cov}(X,Z)$
(c) $\text{cov}(X+c,Y)=\text{cov}(X,Y)$
(d) $\text{cov}(X,Y+c)=\text{cov}(X,Y)$
(e) $\text{cov}(X,Y)=\text{cov}(Y,X)$

(b)의 증명은 (a)의 증명과 거의 같으니, (a)의 증명만 하겠습니다. (a)의 증명은 $(\ast\ast)$로부터 당연합니다 ;

\[\begin{align*} \text{cov}(aX+bY,Z) &=E\left[\left((aX+bY)-(a\mu_X+b\mu_Y)\right)(z-\mu_Z)\right]\\ &=E\left[\left(a(X-\mu_X)+b(Y-\mu_Y)\right)(z-\mu_Z)\right]\\ &=E\left[a(X-\mu_X)(z-\mu_Z)+b(Y-\mu_Y)(z-\mu_Z)\right]\\ &\stackrel{(\ast\ast)}=aE\left[(X-\mu_X)(z-\mu_Z)\right]+bE\left[(Y-\mu_Y)(z-\mu_Z)\right]\\ &=a\text{cov}(X,Z)+b\text{Cov}(Y,Z), \end{align*}\]

(c), (d)의 경우에도 (c)만 증명하겠습니다 ;

\[\begin{align*} \text{cov}(X+c,Y) &=E\left[\left((X+c)-(\mu_X+c)\right)(Y-\mu_Y)\right]\\ &=E\left[(X-\mu_X)(Y-\mu_Y)\right]\\ &=\text{cov}(X,Y). \end{align*}\]

(e)는 covariance의 정의로부터 당연합니다 ;

\[\text{cov}(X,Y) =E\left[(X-\mu_X)(Y-\mu_Y)\right] =E\left[(Y-\mu_Y)(X-\mu_X)\right] =\text{cov}(Y,X).\]

따라서, covariance에 대한 다섯 가지 성질들이 모두 증명되었습니다. $\square$

Pearson correlation coefficient(피어슨 상관계수)

한편, correlation coefficient(상관계수, 피어슨 상관계수, Pearson correlation coefficient)를

\[\rho_{XY}=\frac{\sigma_{XY}}{\sigma_X\sigma_Y}\]

로 정의합니다. 이 값은 두 확률변수가 선형적인 상관관계 (양의 상관관계 / 음의 상관관계)가 얼마나 있는지를 나타내는 지표입니다.

$\rho_{XY}$에 대하여 확인해보는 것은 다음의 두 가지입니다. 이 두 가지 사실을 $X$, $Y$가 이산확률변수일때와 연속확률변수일 때에 대하여 증명해봅니다.

1. $-1\le\rho_{XY}\le1$
2. $X$, $Y$가 선형적인 관계 ($Y=aX+b$)를 가지면 $\rho_{XY}=1(a>0)$, $\rho_{XY}=-1(a<0)$입니다.

$-1\le\rho_{XY}\le1$에 대한 증명은 Cauchy-Scwarz inequality로부터 도출되는데, 증명이 길지 않기는 하지만 식이 꽤 복잡할 수 있습니다. 그래서, 간단한 경우를 먼저 보겠습니다.

$\langle$ 가장 간단한 경우 $\rangle$

두 확률변수 $X$, $Y$와 자연수 $n$에 대하여

\[\begin{align*} P_{XY}(x_1,y_1)&=\frac1n\\ P_{XY}(x_2,y_2)&=\frac1n\\ &\vdots\\ P_{XY}(x_n,y_n)&=\frac1n\\ \end{align*}\]

인 굉장히 간단한 경우(discrete uniform distribution)에

\[\begin{align*} \sigma_X &=\frac1n\sum_{i=1}^n(x_i-\mu_X)^2\\ \sigma_Y &=\frac1n\sum_{i=1}^n(y_i-\mu_Y)^2\\ \text{cov}(X,Y) &=\frac1n\sum_{i=1}^n(x_i-\mu_X)(y_i-\mu_Y) \end{align*}\]

입니다. 한편, 고등학교에서 나오는 Cauchy schwarz inequality는

\[\begin{align*} (a^2+b^2)(x^2+y^2)&\ge(ax+by)^2\\ (a^2+b^2+c^2)(x^2+y^2+z^2)&\ge(ax+by+cz)^2 \end{align*}\]

입니다. 이것을 $n$차원으로 확장하면

\[({a_1}^2+\cdots+{a_n}^2)({b_1}^2+\cdots+{b_n}^2)\ge(a_1b_1+\cdots+a_nb_n)^2\]

이 되고,

\[\left(\sum_i{a_i}^2\right)\left(\sum_i{b_i}^2\right)\ge\left(\sum_i a_ib_i\right)^2\]

이기도 합니다. 여기에 $a_i=x_i-\mu_X$, $b_i=y_i-\mu_Y$를 넣으면

\[\left(\sum_i(x_i-\mu_X)^2\right)\left(\sum_i(y_i-\mu_Y)^2\right)\ge\left(\sum_i(x_i-\mu_X)(y_i-\mu_Y)\right)^2\]

가 됩니다. 양변을 $n^2$으로 나누면

\[\left(\frac1n\sum_i(x_i-\mu_X)^2\right)\left(\frac1n\sum_i(y_i-\mu_Y)^2\right)\ge\left(\frac1n\sum_i(x_i-\mu_X)(y_i-\mu_Y)\right)^2\]

이 되는데, 이것은

\[{\sigma_X}^2{\sigma_Y}^2\ge\sigma_{XY}^2\]

이고, 따라서

\[\sigma_X\sigma_Y\ge\left|\sigma_{XY}\right|\]

입니다. 양변을 $\sigma_X\sigma_Y$로 나누면

\[1\ge\frac{\left|\sigma_{XY}\right|}{\sigma_X\sigma_Y}=|\rho_{XY}|\]

가 되면서 $-1\le\rho_{XY}\le1$이 얻어집니다. 다시 말해, 두 벡터

\[\begin{align*} a&=(a_1,\cdots,a_n)\\ b&=(b_1,\cdots,b_n) \end{align*}\]

에 대한 Cauchy Schwarz inequality인 $|a\cdot b|\le||a||\cdot||b||$ 로부터 결과를 얻은 셈입니다. 이것이, 가장 간단한 경우에 대한 증명입니다.

$\langle$ 이산확률분포 $\rangle$

두 이산확률변수 $X$와 $Y$에 대해서 $X$가 가질 수 있는 값들의 집합을 $C_x$라고 하고, $Y$가 가질 수 있는 값들의 집합을 $C_y$라고 하면, 두 집합의 cartesian product $C_x\times C_y$는 countable이고, 따라서 $C_x\times C_y$를

\[C_x\times C_y=\{(x_1,y_1),(x_2,y_2),\cdots\}\]

로 쓸 수 있습니다. 이때, $C_x\times C_y$는 유한집합(finite, $|C_x\times C_y|=n$)일 수도 있고, 무한집합(countably many)일 수도 있습니다.

만약, $C_x\times C_y$가 유한집합이면 두 벡터 $x,y\in\mathbb R^n$를

\[\begin{align*} x&=\left((x_1-\mu_X)\sqrt{P_{XY}(x_1,y_1)}~~,(x_2-\mu_X)\sqrt{P_{XY}(x_2,y_2)},~~\cdots,~~(x_n-\mu_X)\sqrt{P_{XY}(x_n,y_n)}\right)\\ y&=\left((y_1-\mu_Y)\sqrt{P_{XY}(x_1,y_1)}~~,(y_2-\mu_Y)\sqrt{P_{XY}(x_2,y_2)},~~\cdots,~~(y_n-\mu_Y)\sqrt{P_{XY}(x_n,y_n)}\right)\\ \end{align*}\]

으로 두고, 만약 $C_x\times C_y$가 무한집합이면 두 벡터 $x,y\in\mathbb R^\infty$를

\[\begin{align*} x&=\left((x_1-\mu_X)\sqrt{P_{XY}(x_1,y_1)},~~(x_2-\mu_X)\sqrt{P_{XY}(x_2,y_2)},~~(x_3-\mu_X)\sqrt{P_{XY}(x_3,y_3)},~~\cdots\right)\\ y&=\left((y_1-\mu_Y)\sqrt{P_{XY}(x_1,y_1)},~~(y_2-\mu_Y)\sqrt{P_{XY}(x_2,y_2)},~~(y_3-\mu_Y)\sqrt{P_{XY}(x_3,y_3)},~~\cdots\right)\\ \end{align*}\]

로 둡니다. 그러면, $L^2$ norm $||\cdot||$과 내적 $\langle\cdot,\cdot\rangle$에 대하여

\[\begin{align*} \sigma_X &=||x||\\ \sigma_Y &=||y||\\ \sigma_{XY} &=\langle x,y\rangle \end{align*}\]

입니다. (이때, 내적을 $x\cdot y=\langle x,y\rangle$로 표현했습니다.) 따라서, 피어슨 상관계수는

\[\rho_{XY}=\frac{\sigma_{XY}}{\sigma_X\sigma_Y}=\frac{\langle x,y\rangle}{||x||\cdot||y||}\]

이 됩니다. 그러면 Cauchy-Schwarz inequality \(|\langle x,y\rangle|\le\vert\vert x\vert\vert\cdot\vert\vert y\vert\vert\)에 의해

\[-1\le\rho_{XY}\le1\]

이 됩니다. 또한, $\rho_{XY}=1$인 경우는 두 벡터 $x$, $y$가 같은 방향을 향할 경우이고, $\rho_{XY}=-1$인 경우는 반대 방향을 향할 경우를 말한다는 것도 바로 알 수 있습니다.

$\langle$ 연속확률분포 $\rangle$

$X$, $Y$가 이산확률변수일 경우 $\vert\rho_{XY}\vert\le1$인 사실에 대한 증명은 $\mathbb R^n$과 $\mathbb R^\infty$가 벡터공간이고, 더 나아가 inner product space라는 사실로부터 나옵니다.

$X$, $Y$가 연속확률변수이면, 조금 더 거대한 벡터공간인 함수공간(function space)을 생각해야 합니다. 함수공간

\[\mathbb H=\left\{f\mid f\text{는 }\mathbb R^2\to\mathbb R\text{인 연속함수} \right\}\]

은 벡터공간을 이루고, 어떤 의미에서는 그 차원이 $\mathbb R^\infty$보다도 더 큽니다. 강의에서는 이 집합을 Hilbert space라고 부르는데, Hilbert space는 단순히 벡터공간일 뿐만 아니라 inner product space이기도 합니다 ;

\[\langle f_1,f_2\rangle=\iint_{\mathbb R^2}f_1(x,y)f_2(x,y)\,dx\,dy.\]

두 벡터 $g,h\in\mathbb H$를

\[\begin{align*} g(x,y)&=(x-\mu_X)\sqrt{f_{XY}(x,y)}\\ h(x,y)&=(y-\mu_Y)\sqrt{f_{XY}(x,y)} \end{align*}\]

로 정의하면

\[\begin{align*} \sigma_X &=||g||\\ \sigma_Y &=||h||\\ \sigma_{XY} &=\langle g,h\rangle \end{align*}\]

이 성립하고, 이번에도

\[\rho_{XY}=\frac{\sigma_{XY}}{\sigma_X\sigma_Y}=\frac{\langle g,h\rangle}{||g||\cdot||h||}\]

입니다. 여전히 Cauchy-Schwarz inequality에 의해

\[-1\le\rho_{XY}\le1\]

가 성립합니다. 이로써, 첫번째 사실인 $-1\le\rho_{XY}\le1$이 증명되었습니다. $\square$

다음으로, 두번째 사실을 증명해봅니다. 즉,

$X$와 $Y=aX+b$이면 $\vert\rho_{XY}\vert=1$이며, $a\gt0$일 때 $\rho_{XY}=1$, $a\lt0$일 때 $\rho_{XY}=-1$이다

라는 것을 살펴봅니다. 이것은 $X$, $Y$가 이산확률변수인지 아니면 연속확률변수와는 상관없이 한번에 증명됩니다 ;

\[\begin{align*} \sigma_{XY} &=E\left[(X-\mu_X)(Y-\mu_Y)\right]\\ &=E\left[(X-\mu_X)\left((aX+b)-(a\mu_X+b)\right)\right]\\ &=E\left[(X-\mu_X)\times a(X-\mu_X)\right]\\ &=E\left[a(X-\mu_X)^2\right]\\ &=aE\left[(X-\mu_X)^2\right]\\ &=a{\sigma_X}^2\\[15pt] \sigma_Y &=\sqrt{E\left[(Y-\mu_Y)^2\right]}\\ &=\sqrt{E\left[\left((aX+b)-(a\mu_X+b)\right)^2\right]}\\ &=\sqrt{E\left[a^2(X-\mu_X)^2\right]}\\ &=|a|\sqrt{E\left[(X-\mu_X)^2\right]}\\ &=|a|\sigma_X\\[15pt] \rho_{XY} &=\frac{\sigma_{XY}}{\sigma_X\sigma_Y}\\ &=\frac{a{\sigma_X}^2}{\sigma_X\cdot|a|\sigma_X}\\ &=\frac a{|a|}\\ &=\begin{cases} 1 &(a\gt0)\\ -1 &(a\lt0) \end{cases} \end{align*}\]

13 상관계수와 연합확률분포

13강부터는 내용이 조금 어려워지는 것처럼 보입니다. 그래서 며칠간이나 진도를 나가지 못했습니다. 여기서부터는, 먼저 강의의 내용을 literal하게 적고, 추후에 그 내용을 변경해나갔습니다.

지난 강의에서 두 확률변수 $X$, $Y$에 대한 covariance(공분산) $\sigma_{XY}$, correlation coefficient(Pearson correlation coefficient, 피어슨 상관계수, 상관계수) $\rho_{XY}$를 다음과 같이 정의했었습니다.

\[\begin{align*} \sigma_{XY} &=E\left[(X-\mu_X)(Y-\mu_Y)\right] &&\text{covariance}\\ &=E[XY]-\mu_X\mu_Y\\ \rho_{XY} &=\frac{\sigma_{XY}}{\sigma_X\sigma_Y} &&\text{correlation coefficient} \end{align*}\]

선형대수적인 관점에서 $\sigma_X$와 $\sigma_Y$는 두 벡터의 norm이라고 생각할 수 있었고, $\rho_{XY}$는 그 두 벡터의 내적이라고 생각할 수 있었으므로, Cauchy Schwarz 부등식에 의해 $|\rho_{XY}|\le1$가 성립했습니다.

한편, 만약 $Y$와 $X$가 linear한 (혹은 affine한) 관계에 있을 때, 즉 $Y=aX+b$일 때 ($a\ne0$),

\[\rho_{XY}= \begin{cases} 1 &(a\gt0)\\ -1 &(a\lt0) \end{cases}\]

인 것도 봤습니다.

$\langle 13\rangle$의 맨 처음에는 지난 시간에 정의했던 pearson correlation coefficient에 대한 예시가 나오고 있습니다. 어떤 인구집단 내에서 한 사람을 골라 그 사람의 키를 $X$, 몸무게를 $Y$라고 하겠습니다. 해당 집단의 모든 사람에 대하여 $(X,Y)$를 평면상에 찍으면 아래와 같은 그림이 나올 것입니다.

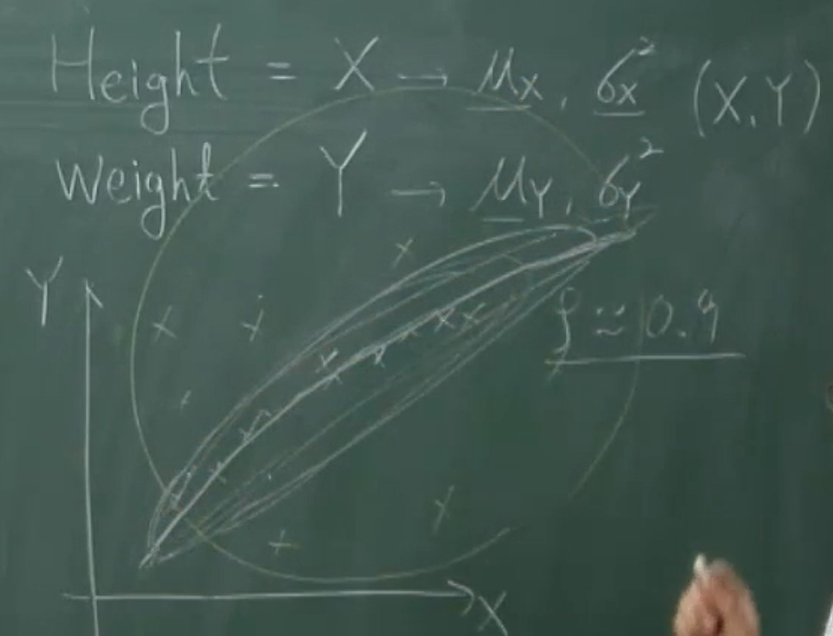
$X$가 증가할 수록 $Y$가 증가하는 경향을 보입니다. 이 경우에 correlation coefficient는 0보다 큰 값을 가지게 됩니다. 왜냐하면, $xy$평면 상에 변량들의 무게중심에 해당하는 $G=(\mu_X,\mu_Y)$를 찍어보면

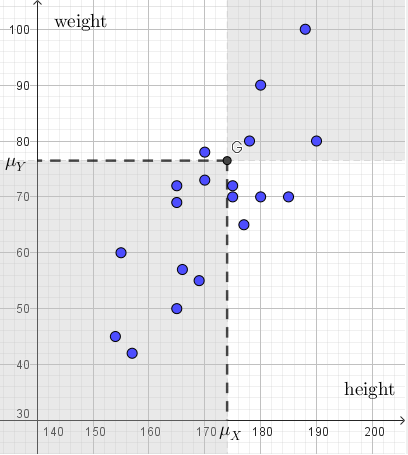
이 됩니다. 만약 $X$가 증가할수록 $Y$가 증가하는 경향을 띤다면, 그러니까 그래프가 우상향하는 경향을 보인다면, $G$의 오른쪽 위 부분(말하자면 1사분면)과 왼쪽 아래 부분(3사분면)에 변량들의 점이 많이 찍힐 것이고, 오른쪽 아랫부분(2사분면)과 왼쪽 윗부분(4사분면)에는 변량들의 점이 적게 찍힐 것입니다. 그런데 covariance를 계산하는 식

\[\begin{align*} \sigma_{XY} &=E\left[(X-\mu_X)(Y-\mu_Y)\right]\\ &=\frac1N\sum_{i=1}^N(x_i-\mu_X)(y_i-\mu_Y) \end{align*}\]

에서, 어떤 변량이 1사분면에 있다면 $x_i\gt\mu_X$, $y_i\gt\mu_Y$일 것이고, 3사분면에 있다면 $x_i\lt\mu_X$, $y_i\lt\mu_Y$일 것이라서, 두 경우 모두

\[(x_i-\mu_X)(y_i-\mu_Y)\gt0\]

일 것입니다. 반면, 어떤 변량이 2사분면에 있거나 4사분면에 있다면

\[(x_i-\mu_X)(y_i-\mu_Y)\lt0\]

일 것입니다. 그런데 변량들의 점들은 1,3사분면에 더 많다고 했으므로, 모든 경우에 대해 $(x_i-\mu_X)(y_i-\mu_Y)$를 더한 값은 0보다 클 것입니다. 따라서, $\sigma_{XY}$는 0보다 클 것이고, $\rho_{XY}$도 마찬가지로 0보다 클 것입니다.

지금까지는 지난 시간 강의에 대한 보충설명이었습니다. 변량들의 무게중심을 중심으로 한 설명은 강의에 있던 내용은 아니고 StatQuest - Covariance, Clearly Explained!!!를 참고해 작성한 것입니다.

5.8 many joint random variables

확률변수 $X_1$, $X_2$, $\cdots$, $X_n$에 대하여, 다음과 같은 확률함수(PMF, PDF)를 생각해볼 수 있습니다.

\[\begin{align*} P_{X_1,\cdots,X_n}(x_1,\cdots,x_n)&(\text{discrete})\\ f_{X_1,\cdots,X_n}(x_1,\cdots,x_n)&(\text{continuous}) \end{align*}\]

두 확률함수들은 다음과 같은 성질들을 만족합니다.

\[\begin{align*} \sum_{x_1}\cdots\sum_{x_n}P_{X_1,\cdots,X_n}(x_1,\cdots,x_n) &=1(\text{discrete})\\ \int_{\mathbb R}\cdots\int_{\mathbb R}f_{X_1,\cdots,X_n}(x_1,\cdots,x_n)\,dx_1\,\cdots,\,dx_n &=1(\text{continuous}) \end{align*}\] \[\begin{align*} P_{X_1,\cdots,X_n}(x_1,\cdots,x_n)&=P\left(X_1=x_1,\cdots,X_n=x_n\right) (\text{discrete})\\ \int_{a_1}^{b_1}\cdots\int_{a_n}^{b_n}f_{X_1,\cdots,X_n}(x_1,\cdots,x_n)\,dx_1\,\cdots,\,dx_n&= P\left(a_1\lt X_1\le b_1,\cdots,a_n\lt X_n\le b_n\right) (\text{continuous}) \end{align*}\]

조건부 확률함수(conditional PMF, conditional PDF)에 관해서는

\[\begin{align*} P_{X_n\vert X_{n-1},X_{n-2},\cdots,X_1}\left(x_n\vert x_{n-1},x_{n-2},\cdots,x_1\right) &=\frac{P_{X_n,X_{n-1},X_{n-2},\cdots,X_1}\left(x_n,x_{n-1},x_{n-2},\cdots,x_1\right)}{P_{X_{n-1},X_{n-2},\cdots,X_1}\left(x_{n-1},x_{n-2},\cdots,x_1\right)} &&(\text{discrete})\\ f_{X_n\vert X_{n-1},X_{n-2},\cdots,X_1}\left(x_n\vert x_{n-1},x_{n-2},\cdots,x_1\right) &=\frac{f_{X_n,X_{n-1},X_{n-2},\cdots,X_1}\left(x_n,x_{n-1},x_{n-2},\cdots,x_1\right)}{f_{X_{n-1},X_{n-2},\cdots,X_1}\left(x_{n-1},x_{n-2},\cdots,x_1\right)} &&(\text{continuous})\\ &=\frac{\partial^n}{\partial x_1\cdots\partial x_n}F_{X_n,\cdots,X_1}\left(x_n,\cdots,x_1\right) \end{align*}\]

와 같은 식을 만족시킵니다. 위 식의 continuous case에 대한 등식에서 처음 두 값이 같다는 것만 강의의 칠판에 적혀있습니다.

강의에서는 이러한 여러 개의 확률변수가 통신공학이나 역학에서 어떻게 활용되는지가 더 설명됩니다. 위와 같이 확률변수 여러 개의 확률변수들 (혹은 그것들의 집합)을 확률과정(stochastic process)이라고 합니다. 즉, $X_t$들의 집합

\[\{X_t\}_{t\in T}\]

이 확률과정입니다. 위에서는 $t$가 $1$, $2$, $\cdots$, $n$과 같은 값을 가졌습니다. 즉 index set인 $T$가 $T=\{1,2,\cdots,n\}$인 것입니다. 일반적으로 $T$는 실수집합 $\mathbb R$의 부분집합으로 봅니다. 그러니까, 위의 예처럼 유한집합이 될 수도 있고 ; $T=\{1,2,\cdots,n\}$, countable 집합이 될 수도 있으며 ; $T=\{1,2,\cdots\}$, 아니면 양의 실수의 집합이 될 수도 있습니다 ; $T=\{t\in\mathbb R:t>0\}$.

만약 $t$를 시간으로 해석하고, $X_t$를 어떤 물체에 대한 물리적인 양으로 생각한다면, 확률과정은 이 물체와 관련된 어떤 현상을 해석하는 데 사용될 수 있습니다. 강의에서는 미사일이 날아가는 과정을 확률과정을 통해 해석할 수 있다고 말합니다. 그러니까, $X_t$를 시각 $t$에서의 미사일의 위치라고 한다면 (물론, 미사일은 3차원 공간 안에 위치하므로, 세 개의 확률과정을 생각하거나 세 종류의 확률변수를 생각해야 합니다.) $E[X_t]$를 통해 이 미사일이 이동할 예상 궤적을 생각해볼 수 있고, 각각의 시각 $t$에서 미사일이 특정한 영역 내에 위치할 확률을 계산할 수도 있습니다.

이 미사일의 예에서 $X_t$들은 독립조건을 만족시키지 않습니다. 만약 brownian motion의 경우라면, $X_t$들은 각각 독립적일 수도 있겠지만, 미사일의 예에서 $X_t$, 즉 시각 $t$에서의 위치는 이전의 시각에서의 위치인 $X_{t-1}$, $X_{t-2}$ 등에 영향을 받을 수밖에 없습니다. 그런 의미에서

\[f_{X_t|X_{t-1},X_{t-2}}(x_t\vert x_{t-1}, x_{t-2})\]

와 같은 조건부확률을 생각할 수밖에 없다는 사실이 강의에서 설명됩니다. 이러한 확률과정 중에서, 바로 이전 시각에 대한 영향만 고려하는 경우의 stochastic process(확률과정)을 markov process(마르코프 과정, markov chain)이라고 부릅니다. 다시 말해, 위의 식에서 현재 시점에서의 상태 $X_t$는 바로 이전 시점과 그 이전의 시점과의 연관성만을 고려했습니다. 그러니까, $X_t$는 $X_{t-3}$, $X_{t-4}$, $\cdots$ 등과는 독립적이라는 가정을 내포하고 있습니다. 반면, markov process은

\[f_{X_t|X_{t-1}}(x_t\vert x_{t-1})\]

와 같이 모델링하는 것입니다. 현재 시점에서의 상태 $X_t$가 바로 이전 시점의 상태 $X_{t-1}$에만 의존한다는 가정 하에 문제를 보는 것입니다.

5.9 multinomial distribution

이전에 $\langle07\rangle$에서 이항분포(binomial distribution)이란, 여러 번의 독립적인 Bernoulli trial에 대하여 성공횟수의 분포를 말했습니다. 즉, $n$번의 Bernoulli trial에 대하여, 각각의 Bernoulli trial의 성공확률이 $p$일 때, $n$번 중에서 성공한 횟수를 $X$라고 할 때, $X$는

\[P_X(x)=\binom nxp^x(1-p)^{n-x},\quad(x=0,1,2,\cdots,n)\]

를 PMF로 가진다고 했었습니다. 이때, PMF의 식에 $\binom nx$와 같은 조합의 수가 나타났었습니다. 한편, $\langle02\rangle$에서 조합의 수는 ‘같은 것이 포함된 순열’의 특수한 경우라고 했었습니다.

만약, binomial distribution에서 Bernoulli trial (binary trial)이었던 것을 multinary trial로 바꾸면 multinomial distribution이라고 하는 개념을 생각해볼 수 있고, 그때 조합의 수 대신 ‘같은 것이 포함된 순열’이 나타납니다.

다시 말해, 하나의 시행에서 나올 수 있는 outcome의 개수가 (2개가 아닌) 여러 개인 경우를 생각해볼 수 있습니다. 대표적으로 trinomial distribution의 경우 (outcome의 개수가 3개인 경우)를 보겠습니다. 결과가 $A$, $B$, $C$로 나타날 수 있는 어떤 시행(ternary trial)을 독립적으로 $n$번 시행할 때, 각 시행에서 $A$가 나타날 확률을 $p_A$, $B$가 나타날 확률을 $p_B$라고 하면 $C$가 나타날 확률은 $1-p_A-p_B$입니다. $A$가 $N_A$번, $B$가 $N_B$번 나타난다고 할 때, $N_A$, $N_B$는 각각 이산확률변수이고, 그 joint PMF가

\[P_{N_A,N_B}(n_A,n_B)=\frac{n!}{n_A!n_B!(n-n_A-n_B)!}{p_A}^{n_A}{p_B}^{n_B}(1-p_A-p_B)^{n-n_A-n_B}\]

로 주어집니다. 이때 $\frac{n!}{n_A!n_B!(n-n_A-n_B)!}$의 값은

\[\binom n{n_A,n_B}=\frac{n!}{n_A!n_B!(n-n_A-n_B)!}\]

와 같이 쓰기도 합니다.

일반적으로, $k$개의 서로다른 outcome $A_1$, $A_2$, $\cdots$, $A_k$이 나올 수 있는 시행에 대하여, 각각의 outcome $A_i$가 나타날 확률이 $p_i$로 주어지고, $n$번의 독립시행에서 $A_i$가 $N_i$번 나타난다고 할 때, $N_i$는 모두 이산확률변수입니다. 그때, $N_1$, $\cdots$, $N_k$의 joint PMF는

\[\begin{align*} P_{N_1,N_2,\cdots,N_k}(n_1,n_2,\cdots,n_k) &=\frac{n!}{n_1!n_2!\cdots n_k!}{p_1}^{n_1}{p_2}^{n_2}\cdots{p_k}^{n_k}\\ &=\binom n{n_1,n_2,\cdots,n_k}\prod_{i=1}^n{p_i}^{n_i} \end{align*}\]

로 주어집니다.

위의 식에서 $$\binom n{n_1,n_2,\cdots,n_k}=\frac{n!}{n_1!n_2!\cdots n_k!}$$ 와 같이 정의된 값을 multinomial coefficient라고 부릅니다. 조합의 수 $\binom nr$을 binomial coefficient(이항계수)라고 불렀던 것의 연장선입니다.
비슷한 맥락에서 이항정리(binomial theorem)에 대응되는 다항정리(multinomial theorem) 도 생각해볼 수 있습니다. 이항정리가 두 개의 항의 합 $(a+b)^n$에 대한 거듭제곱의 전개식을 설명한다면 다항정리는 $n$개의 항의 합 $(x_1+x_2+\cdots+x_k)^n$에 대한 거듭제곱의 전개식을 설명합니다 ; $$(x_1+x_2+\cdots+x_k)^n=\sum_{n_1+\cdots+n_k=n}\binom n{n_1,\cdots,n_k}\prod_{i=1}^n{x_i}^{n_k}.$$

bivariate normal distribution(bivariate Gaussian distribution)

강의의 마지막에 등장하는 것은 bivariate normal distribution과 multivariate normal distribution에 대한 내용입니다. 해당 내용들은 워낙 많은 것들을 함축하고 있어서, 그 의미에 대해 다 설명하기는 쉽지 않습니다. 그래도, bivariate normal distribution에 관해서는 나름대로 공부해보고, 해당 내용들을 TeX파일로 만들어보았습니다. 이것은, DeGroot, Probability and Statistics, 4ed의 내용을 참고하여 bivariate normal distribution에 관한 주요 사항들과 그 증명에 필요한 사항들을 적어본 것입니다. 책에는 $n$개의 확률변수에 대해 적혀있는데 그것을 $2$개의 확률변수로 바꾸어서 적어놓은 것입니다. 링크

이번 절에서는 강의의 내용을 따라가되, 강의에서 제시한 짤막한 소개를 보충하는, 정확한 statement를 소개해보았습니다.

bivariate normal distribution
다섯 개의 수 $\mu_X$, $\mu_Y$, $\sigma_X$, $\sigma_Y$, $\rho$가 $\mu_X,\mu_Y\in\mathbb R$, $\sigma_X,\sigma_Y\gt0$, $-1\lt\rho\lt1$를 만족시키고, $X$, $Y$가 연속확률변수일때, $X$, $Y$의 joint PDF가 $$ f_{XY}(x,y)=\frac1{2\pi\sigma_X\sigma_Y\sqrt{1-\rho^2}}\exp\left(-\frac1{2(1-\rho^2)}\left[\left(\frac{x-\mu_X}{\sigma_X}\right)^2-2\rho\left(\frac{x-\mu_X}{\sigma_X}\right)\left(\frac{y-\mu_Y}{\sigma_Y}\right)+\left(\frac{y-\mu_Y}{\sigma_Y}\right)^2\right]\right) \tag{$\ast$} $$ 와 같이 주어지면 $X$, $Y$의 분포를 bivariate normal distribution이라고 부릅니다. 또한, 이 경우에 $$ \begin{align*} X&\sim N(\mu_X,{\sigma_X}^2)\\ Y&\sim N(\mu_Y,{\sigma_Y}^2)\\ \rho_{XY}&=\rho \end{align*} $$ 가 성립합니다.

이 강의에서의 notation을 계속 따라가고 있기 때문에 위의 statement는 그 뜻이 조금 명확하지 않게 적혀져있습니다. 이 강의에서 $\mu_X$와 $\sigma_X$는 항상, 각각 $X$의 평균과 표준편차를 의미했습니다. 하지만 위의 statement에서 첫번째 줄에서 $\mu_X$, $\mu_Y$, $\sigma_X$, $\sigma_Y$를 언급할 때, 이것들은 단지 다섯 개의 실수를 언급할 뿐이지 $X$와 $Y$의 평균이나 표준편차라는 의미는 아직 없습니다. 그런데 만약 $(\ast)$ 식이 PDF로 주어진다면, 이 숫자들이 평균과 표준편차의 의미를 가진다는 것이 위 statement의 내용입니다. 강의의 notation을 따라가기 위해서, 그리고 너무 statement가 길어지지 않게 하기 위해서 위와 같이 적어보았습니다.

bivariate normal distribution에 대한 위의 statement는 $\langle09\rangle$의 마지막 부분에서 증명한 ‘정규분포를 따르는 확률변수들의 일차결합은 정규분포이다’라는 성질과 $\langle12\rangle$에서 증명한 covariance의 bilinearity로부터 다음과 같이 증명될 수 있습니다.

새 확률변수 $U$, $V$를

\[\begin{align*} U&=\frac{X-\mu_X}{\sigma_X}\\ V&=\frac1{\sqrt{1-\rho^2}}\left(-\rho\frac{X-\mu_X}{\sigma_X}+\frac{Y-\mu_Y}{\sigma_Y}\right) \end{align*}\]

로 정의하면

\[\begin{align*} x&=\sigma_Xu+\mu_Y\\ y&=\sigma_Y\left(\rho u+\sqrt{1-\rho^2}v\right)+\mu_Y \end{align*}\]

로부터

\[\begin{align*} \frac{\partial(x,y)}{\partial(u,v)} &=\begin{vmatrix} \frac{\partial x}{\partial u}&\frac{\partial x}{\partial v}\\[5pt] \frac{\partial x}{\partial u}&\frac{\partial y}{\partial v} \end{vmatrix}\\ &=\frac{\partial x}{\partial u}\times\frac{\partial y}{\partial v} -\frac{\partial x}{\partial v}\times\frac{\partial y}{\partial u}\\ &=\sigma_X\times\sigma_Y\sqrt{1-\rho^2}-0\times\sigma_Y\rho\\ &=\sigma_X\sigma_Y\sqrt{1-\rho^2} \end{align*}\]

입니다. 그러면

\[\begin{align*} f_{UV}(u,v) &\stackrel\star=f_{XY}(x,y)\left|\frac{\partial(x,y)}{\partial(u,v)}\right|\\ &=f_{XY}\left(\sigma_Xu+\mu_Y,\sigma_Y\left(\rho u+\sqrt{1-\rho^2}v\right)+\mu_Y\right)\left|\frac{\partial(x,y)}{\partial(u,v)}\right|\\ =&\frac1{2\pi}\exp\Biggl\{-\frac1{2(1-\rho^2)}\biggl[ u^2-2\rho u(\rho u+\sqrt{1-\rho^2}v)+(\rho u+\sqrt{1-\rho^2}v)^2\biggr]\Biggr\}\\ =&\frac1{2\pi}\exp\Biggl\{-\frac1{2(1-\rho^2)}\biggl[u^2-\rho u^2+(1-\rho^2)v^2\biggr]\Biggr\}\\ =&\frac1{2\pi}\exp\Biggl\{-\frac12(u^2+v^2)\Biggr\}\\ \end{align*}\]

입니다. 이때, $\star$는 $\langle17\rangle$에서 다루어집니다. 간단하게 설명하면

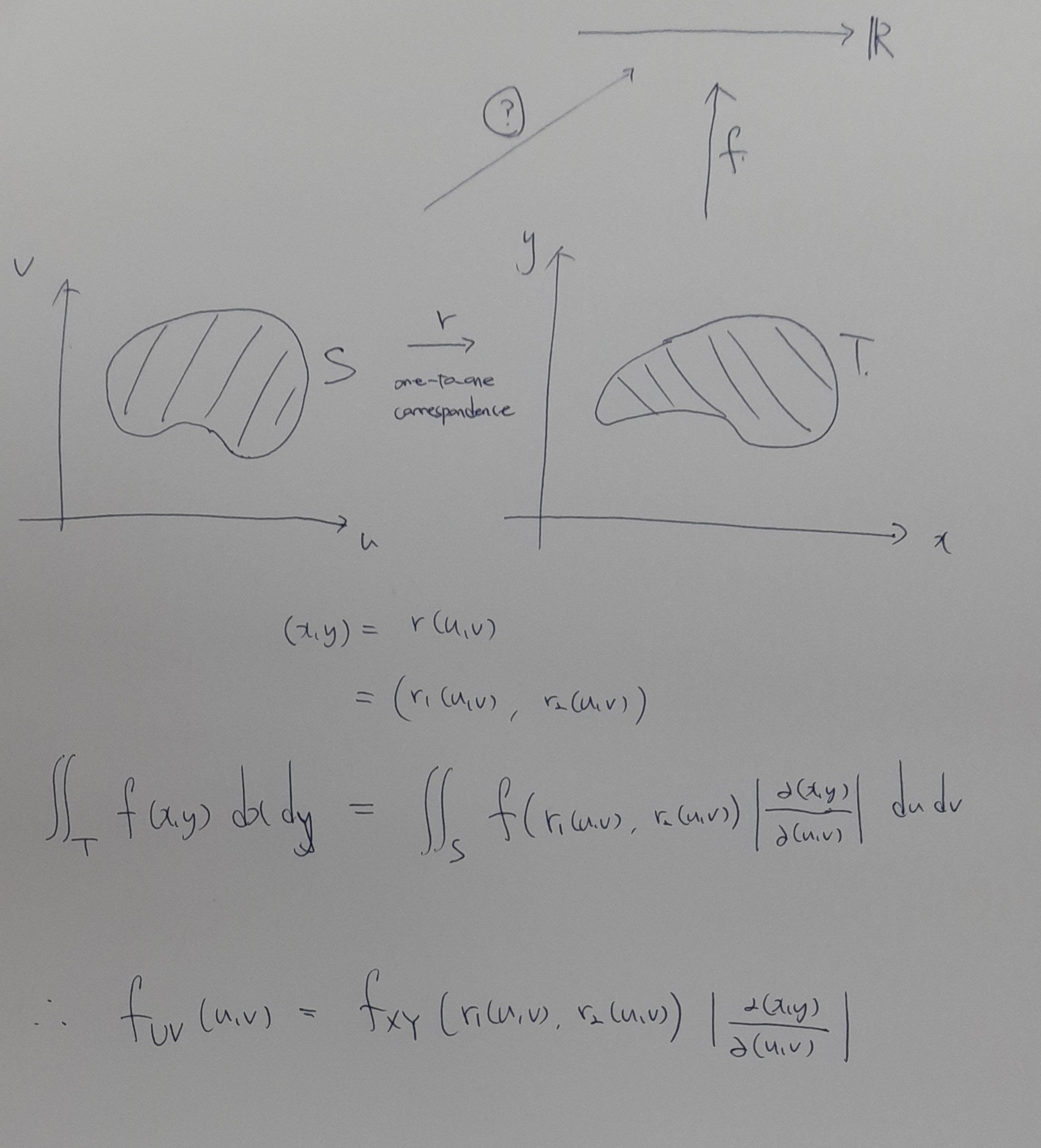
와 같이 말할 수 있습니다. 따라서

\[\begin{align*} f_V(v) &=\int_{\mathbb R}f_{UV}(u,v)\,dv\\ &=\frac{e^{-\frac12u^2}}{2\pi}\int_{\mathbb R}e^{-\frac12v^2}\,dv\\ &=\frac{e^{-\frac12u^2}}{2\pi}\times\sqrt{2\pi}\\ &=\frac1{\sqrt{2\pi}}e^{-\frac12u^2} \end{align*}\]

이고, 마찬가지로

\[f_V(v)=\frac1{\sqrt{2\pi}}e^{-\frac12v^2}.\]

입니다. 따라서, $U$와 $V$는 standard normal이고 독립입니다.

그러면, $X=\sigma_XU+\mu_X$이고 $U\sim N(0,1)$이므로 $X$는 평균이

\[E[X]=\sigma_X\times0+\mu_X=\mu_X\]

이고, 분산이

\[V[X]={\sigma_X}^2\times1^2={\sigma_X}^2.\]

인 정규분포를 따름을 알 수 있습니다. 또한, $Y=\sigma_Y\left(\rho U+\sqrt{1-\rho^2}V\right)+\mu_Y$이고 $V\sim N(0,1)$, $\text{cov}(U,V)=0$이므로 $Y$는 평균이

\[E[Y]=\sigma_Y\rho\times0+\sigma_Y\sqrt{1-\rho^2}\times0+\mu_Y=\mu_Y\]

이고 분산이

\[V[Y]={\sigma_Y}^2\rho^2\times1^2+{\sigma_Y}^2(1-\rho^2)\times1^2={\sigma_Y}^2.\]

인 정규분포를 따름을 알 수 있습니다. 즉, $X\sim N(\mu_X,{\sigma_X}^2)$이고 $Y\sim N(\mu_Y,{\sigma_Y}^2)$입니다.

마지막으로 $\rho_{XY}$를 계산해보면,

\[\begin{align*} \text{Cov}(X,Y) &=\text{Cov}\left(\sigma_XU+\mu_X,\sigma_Y\rho U+\sigma_Y\sqrt{1-\rho^2}V+\mu_Y\right)\\ &=\text{Cov}\left(\sigma_XU,\sigma_Y\rho U+\sigma_Y\sqrt{1-\rho^2}V\right)\\ &=\text{Cov}\left(\sigma_XU,\sigma_Y\rho U\right)+\text{Cov}\left(\sigma_XU,\sigma_Y\sqrt{1-\rho^2}V\right)\\ &=\sigma_X\sigma_Y\rho\text{Cov}\left(U,U\right)+\sigma_X\sigma_Y\sqrt{1-\rho^2}\text{Cov}\left(U,V\right)\\ &=\sigma_X\sigma_Y\rho\times1+\sigma_X\sigma_Y\sqrt{1-\rho^2}\times0\\ &=\sigma_X\sigma_Y\rho \end{align*}\]

이 되어 $\rho_{XY}=\rho$가 성립합니다. $\square$

$\langle13\rangle$에서 두 확률변수 $X$, $Y$가 독립이면 uncorrelated하다고 했었고, 그 역은 꼭 성립하지는 않는다고 했습니다. 하지만, bivariate normal인 경우에는 그 역이 성립합니다. 즉

bivariate normal distribution을 따르는 두 확률변수가 uncorrelated이면, 독립입니다.

왜냐하면, $X$와 $Y$가 uncorrelated하다고 가정하면, $\rho=0$입니다. 이것을 위의 식에 대입하면

\[\begin{align*} f_{XY}(x,y) &=\frac1{2\pi\sigma_X\sigma_Y\sqrt{1-\rho^2}}\exp\left(-\frac1{2(1-\rho^2)} \left[\left(\frac{x-\mu_X}{\sigma_X}\right)^2-2\rho\left(\frac{x-\mu_X}{\sigma_X}\right)\left(\frac{y-\mu_Y}{\sigma_Y}\right)+\left(\frac{y-\mu_Y}{\sigma_Y}\right)^2\right]\right)\\ &=\frac1{2\pi\sigma_X\sigma_Y}\exp\left(-\frac12 \left[\left(\frac{x-\mu_X}{\sigma_X}\right)^2+\left(\frac{y-\mu_Y}{\sigma_Y}\right)^2\right]\right)\\ &=\frac1{\sqrt{2\pi}\sigma_X}\exp\left(-\frac12\left(\frac{x-\mu_X}{\sigma_X}\right)^2\right) \times\frac1{\sqrt{2\pi}\sigma_Y}\exp\left(-\frac12\left(\frac{y-\mu_Y}{\sigma_Y}\right)^2\right)\\ &=f_X(x)f_Y(y) \end{align*}\]

이 되어 $X$와 $Y$가 독립이라고 말할 수 있기 때문입니다.

강의에서는 bivariate normal distribution에 대한 그래프의 모양에 대한 언급이 있습니다. 직접 그래프를 한 번 찾아봤습니다. 아래 그림은 함수 $f_{XY}$에 대한 그래프입니다.

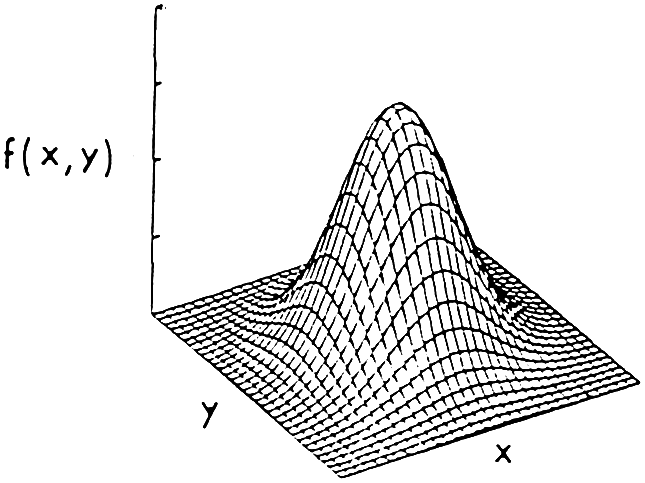
강의에서는 그래프의 모양이 마치 봉분처럼 보인다고 말합니다. 또한, CDF는 아래 그림과 같이 나타납니다.

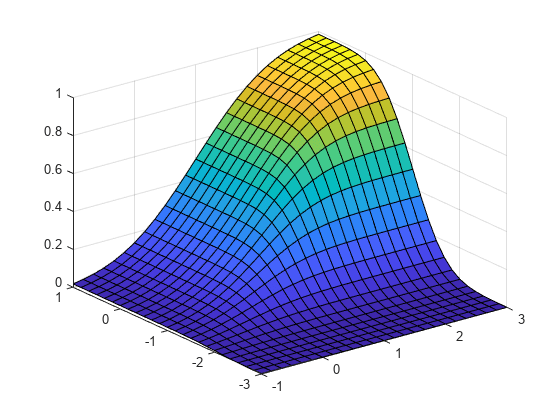
하지만, PDF의 그래프는 위에서 보는 것과 같이 꼭 대칭적으로 나타나지는 않습니다. 그러니까, PMF 그래프의 등고선을 그렸을 때 원이 나오기도 하지만 일반적으로는 타원이 나옵니다. 그리고 그 타원의 장축과 단축의 방향이 꼭 $x$축과 $y$축의 방향과 일치할 필요는 없습니다. 예를 들어, 다음과 같은 PDF가 나올 수도 있는 것입니다.

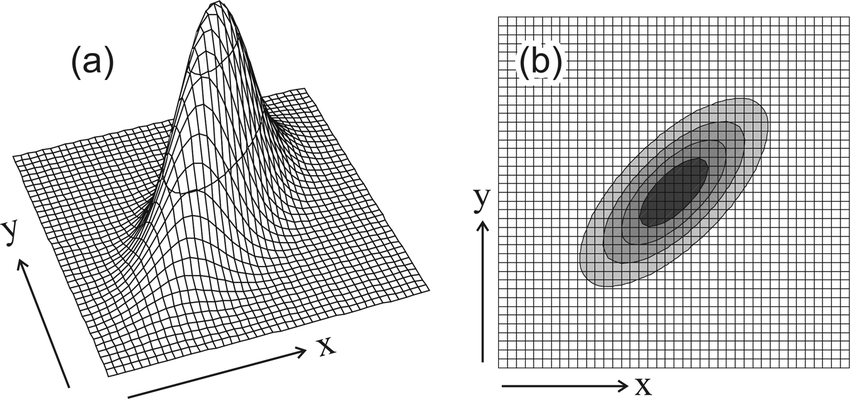
또한, 아래 그림에서는 bivariate normal distribution의 marginal distribution $P_X(x)$, $P_Y(y)$를 표현하고 있습니다. 그림상으로 보면 marginal distribution들은 각각 정규분포를 따르는 것처럼 보입니다. 이것은 위의 정리에서 $X\sim N(\mu_X,{\sigma_X}^2)$, $Y\sim N(\mu_Y,{\sigma_Y}^2)$라고 말했던 것에 해당합니다.

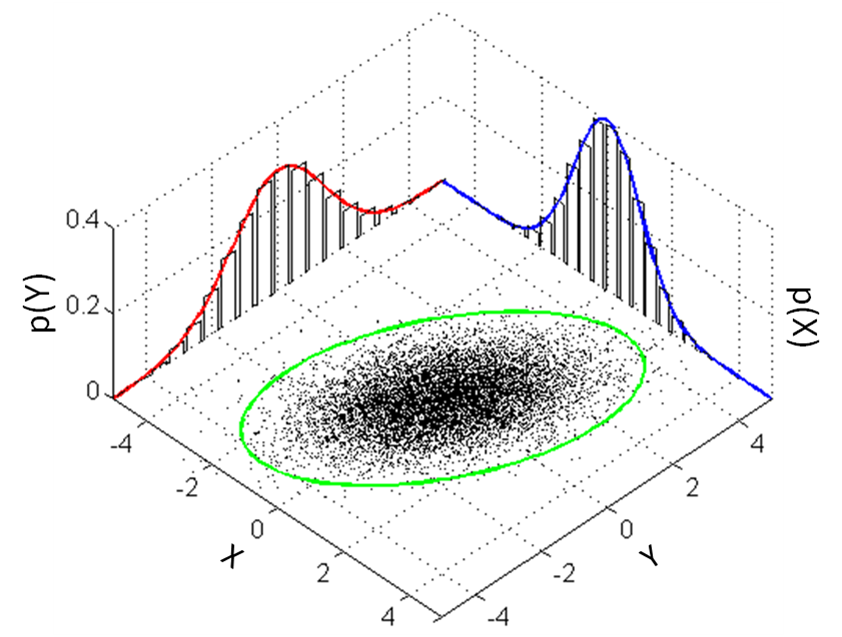
또한, 등고선 위의 타원의 장축(혹은 단축)이 $x$축 (혹은 $y$축)과 얼마만큼의 각도($\theta$)로 떨어져있는지 하는 것은 $\rho$의 값과 관련되어 있다는 언급 또한 나옵니다. 이때, $\theta$는

\[\theta=\frac12\tan^{-1}\left[\frac{2\rho\sigma_X\sigma_Y}{~{\sigma_X}^2-{\sigma_Y}^2}\right]\]

로 주어진다고 합니다. 이에 대한 유도가 강의에서는 과제로 주어지고 있고, 회전변환을 잘 사용하면 이것을 증명할 수 있다는 언급이 있습니다만, 이 포스트에서는 과제를 풀지는 않겠습니다.

multivariate normal distribution(multivariate Gaussian distribution)

이번에는 변수가 2개가 아니라 여러 개일때의 joint distribution에 대해 다룹니다. 다음 정리는, binvariate normal distribution에 대한 정리를 확장해서 적어놓은 것인데, 조금의 확인이 더 필요할 것 같습니다. 일단 적어보면,

multivariate normal distribution
$X_1$, $\cdots$, $X_n$이 모두 연속확률변수이고, 각각의 $i\in\{1,\cdots,n\}$에 대하여 $\mu_{X_i}=\mu_i\in\mathbb R$, $\sigma_{X_i}=\sigma_i\gt0$이며, 각각의 $i,j\in\{1,\cdots,n\}$에 대하여 $-1\lt\rho_{X_i,X_j}=\rho_{ij}\lt1$이라고 가정하겠습니다. 만약, $X_1$, $\cdots$, $X_n$의 joint PDF가 $$ f_{X_1,\cdots,X_n}(x_1,\cdots,x_n) =\frac{|{\mathbb C}^{-1}|^{\frac12}}{(2\pi)^{\frac n2}}\exp \left\{-\frac12 (\boldsymbol x-\overline{\boldsymbol x})^T {\mathbb C}^{-1} (\boldsymbol x-\overline{\boldsymbol x}) \right\} $$ 와 같이 주어지면, $X_1$, $\cdots$, $X_n$의 분포를 multivariate normal distribution이라고 부릅니다. 이때, 각각의 $i\in\{1,\cdots,n\}$에 대하여 $X_i\sim N(\mu_i,{\sigma_i}^2)$이 성립합니다.

위의 정리 및 정의에서,

\[\boldsymbol x = \begin{bmatrix} x_1\\\vdots\\x_n \end{bmatrix}\]

이고,

\[\begin{align*} \overline{\boldsymbol x} = \begin{bmatrix} \mu_1\\ \vdots\\ \mu_n \end{bmatrix} \end{align*}\]

이며,

\[\begin{align*} \mathbb C &=\left[\sigma_{ij}\right]_{n\times n} &=\begin{bmatrix} \sigma_{11} &\cdots&\sigma_{1n}\\ \vdots &\ddots&\vdots\\ \sigma_{n1} &\cdots&\sigma_{nn}\\ \end{bmatrix} \end{align*}\]

입니다. 그러니까, $\mathbb C$는 복소수들의 집합이 아닙니다. $\mathbb C$는 covariance matrix(공분산행렬)이라고 불립니다. $\text{Cov}(X,Y)=\text{Cov}(Y,X)$이므로, $\mathbb C$는 symmetric matrix입니다. 따라서, eigenvalue들은 모두 실수이고, eigenvector들이 모두 직교하며, 항상 orthogonally diagonalizable합니다. 이를 통해 basis vector들을 쉽게 구할 수 있고 이를 통해 신호처리 등에서의 모델링을 할 때 쉽게 된다는 말씀도 강의에서 언급되고 있습니다.

확률변수 $X_1$, $\cdots$, $X_n$ 들을 벡터로 만들어놓은 것을 random vector라고 합니다. 즉,

\[\boldsymbol X= \begin{bmatrix} X_1\\ \vdots\\ X_n \end{bmatrix}\]

은 random vector입니다. 그러면, $X_1$, $\cdots$, $X_n$이 multivariate normal distribution을 따른다는 것을

\[\boldsymbol X\sim N(\overline{\boldsymbol x},\mathbb C)\]

로 간단히 쓰기도 합니다.

multivariate PDF의 식

\[f_{X_1,\cdots,X_n}(x_1,\cdots,x_n) =\frac{|{\mathbb C}^{-1}|^{\frac12}}{(2\pi)^{\frac n2}}\exp \left\{-\frac12 (\boldsymbol x-\overline{\boldsymbol x})^T {\mathbb C}^{-1} (\boldsymbol x-\overline{\boldsymbol x}) \right\}\]

에 $n=1$을 대입하면 ($X_1=X$)

\[\begin{align*} \mathbb C &=\begin{bmatrix}\sigma_{11}\end{bmatrix} =\begin{bmatrix}{\sigma_X}^2\end{bmatrix}\\ \mathbb C^{-1} &=\begin{bmatrix}\frac1{~{\sigma_X}^2}\end{bmatrix}\\ \left|\mathbb C^{-1}\right| &=\frac1{~{\sigma_X}^2}\\ \boldsymbol x &=\begin{bmatrix}x\end{bmatrix}\\ \overline{\boldsymbol x} &=\begin{bmatrix}\mu_X\end{bmatrix}\\ \boldsymbol x-\overline{\boldsymbol x} &=\begin{bmatrix}x-\mu_X\end{bmatrix}\\ (\boldsymbol x-\overline{\boldsymbol x}) \mathbb C^{-1} (\boldsymbol x-\overline{\boldsymbol x})^T &=\begin{bmatrix}x-\mu_X\end{bmatrix} \begin{bmatrix}\frac1{~{\sigma_X}^2}\end{bmatrix} \begin{bmatrix}x-\mu_X\end{bmatrix}\\ &=\begin{bmatrix}\frac{(x-\mu_X)^2}{~{\sigma_X}^2}\end{bmatrix}\\ f_X(x) &=\frac{|{\mathbb C}^{-1}|^{\frac12}}{(2\pi)^{\frac 12}}\exp \left\{-\frac12 (\boldsymbol x-\overline{\boldsymbol x})^T {\mathbb C}^{-1} (\boldsymbol x-\overline{\boldsymbol x}) \right\}\\ &=\frac1{\sigma_X\sqrt{2\pi}}\exp\left\{ -\frac12\left({\frac{x-\mu_X}{\sigma_X}}\right)^2 \right\} \end{align*}\]

이 되어 univariate normal PDF의 식과 일치합니다.

$n=2$을 대입하면 ($X_1=X$, $X_2=Y$)

\[\begin{align*} \mathbb C &=\begin{bmatrix} \sigma_{11}&\sigma_{12}\\ \sigma_{21}&\sigma_{22} \end{bmatrix} =\begin{bmatrix} {\sigma_X}^2&\sigma_{XY}\\ \sigma_{XY}&{\sigma_Y}^2 \end{bmatrix}\\ |\mathbb C| &={\sigma_X}^2{\sigma_Y}^2-{\sigma_{XY}}^2\\ &={\sigma_X}^2{\sigma_Y}^2(1-\rho^2)\\ \mathbb C^{-1} &=\frac1{~{\sigma_X}^2{\sigma_Y}^2(1-\rho^2)} \begin{bmatrix} {\sigma_Y}^2&-\sigma_{XY}\\ -\sigma_{XY}&{\sigma_X}^2 \end{bmatrix}\\ \boldsymbol x &=\begin{bmatrix} x\\ y \end{bmatrix}\\ \overline{\boldsymbol x} &=\begin{bmatrix} \mu_X\\ \mu_Y \end{bmatrix}\\ \boldsymbol x-\overline{\boldsymbol x} &=\begin{bmatrix} x-\mu_X\\ y-\mu_Y \end{bmatrix}\\ (\boldsymbol x-\overline{\boldsymbol x})^T \mathbb C^{-1} (\boldsymbol x-\overline{\boldsymbol x}) &=\frac1{~{\sigma_X}^2{\sigma_Y}^2(1-\rho^2)} \begin{bmatrix} x-\mu_X& y-\mu_Y \end{bmatrix} \begin{bmatrix} {\sigma_Y}^2&-\sigma_{XY}\\ -\sigma_{XY}&{\sigma_X}^2 \end{bmatrix} \begin{bmatrix} x-\mu_X\\ y-\mu_Y \end{bmatrix}\\ &=\frac1{~{\sigma_X}^2{\sigma_Y}^2(1-\rho^2)} \left[{\sigma_Y}^2(x-\mu_X)^2-2\sigma_{XY}(x-\mu_X)(y-\mu_Y)+{\sigma_X}^2\right]\\ &=\frac1{1-\rho^2} \left[\left(\frac{x-\mu_X}{\sigma_X}\right)^2-2\rho\left(\frac{x-\mu_X}{\sigma_X}\right)\left(\frac{y-\mu_Y}{\sigma_Y}\right)+\left(\frac{y-\mu_Y}{\sigma_Y}\right)^2\right]\\ f_{XY}(x,y) &=\frac1{2\pi\sigma_X\sigma_Y\sqrt{1-\rho^2}}\exp\left(-\frac1{2(1-\rho^2)}\left[\left(\frac{x-\mu_X}{\sigma_X}\right)^2-2\rho\left(\frac{x-\mu_X}{\sigma_X}\right)\left(\frac{y-\mu_Y}{\sigma_Y}\right)+\left(\frac{y-\mu_Y}{\sigma_Y}\right)^2\right]\right) \end{align*}\]

가 되어 bivariate normal PDF와 일치합니다.

14 확률변수의 변환함수

이번 강의에서는 $X$의 확률분포가 주어질 때, $Y=g(X)$의 확률분포가 어떻게 나타나는지, 그리고 $E[g(X)]$가 어떻게 계산되는지 다룹니다. $E[g(X)]$는 $\langle03\rangle$에서 언급한 LOTUS의 식으로 쉽게 계산될 수 있다고 했었습니다. 하지만, $Y=g(X)$의 확률분포는 그렇게까지 간단하게 얻어지지 않습니다.

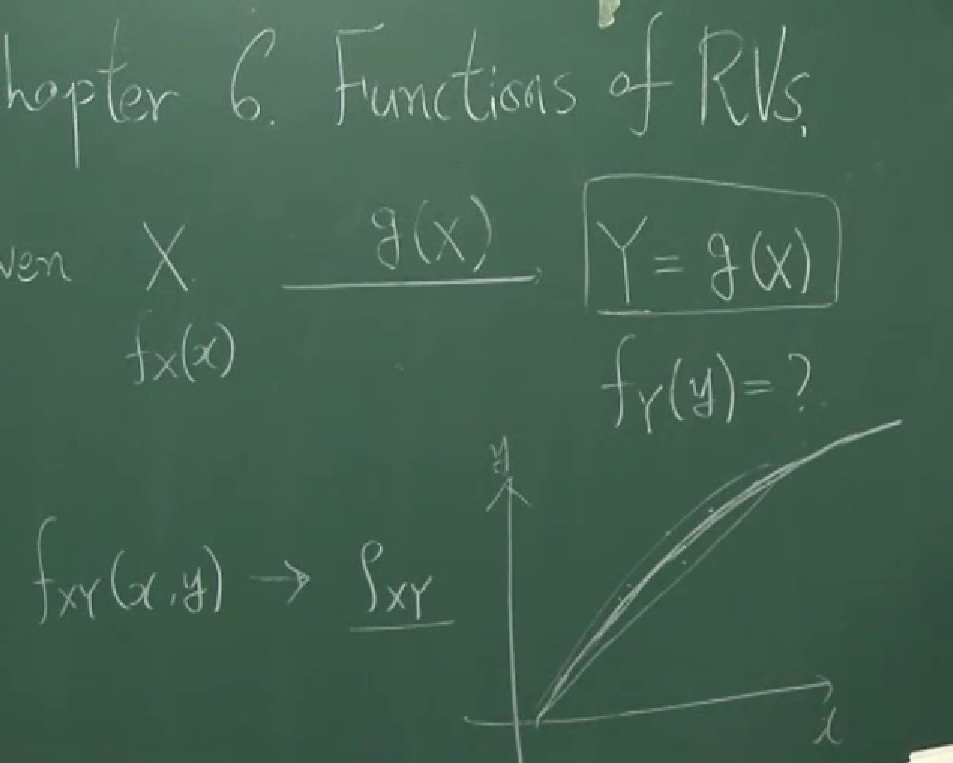
앞서 강의들에서 두 확률변수 $X$, $Y$에 대한 correlation coefficient $\rho_{XY}$를 공부했었습니다. $\rho_{XY}$는 두 변수간의 ‘관계’를 말해줍니다. 이번에는 더 나아가, 두 변수간의 ‘함수’ $Y=g(X)$가 주어졌을 때의 경우를 다루는 것입니다. 이 주제는 이번 강의를 포함한 다섯 번의 강의의 주제이기도 합니다. 지금은 $g:\mathbb R\to\mathbb R$인 함수를 이야기하고 있는데 이것을 $g:\mathbb R^n\to\mathbb R$인 경우와 $g:\mathbb R^m\to\mathbb R^n$인 경우로까지 확장하며, 그 과정에서 convolution, Jacobian, Fourier transformation 등의 주제가 언급된다고 합니다.

예를 들어, 0과 1 사이의 uniform distribution을 따르는 값 $X$는 (프로그래밍적으로) 쉽게 만들어낼 수 있다고 합니다. 만약, 적절한 함수 $g:\mathbb R\to\mathbb R$이 있어서 $Y=g(X)$가 normal distribution을 따를 수 있게 한다면, uniform distribution의 수를 생성해내는 것 만으로도 normal distribution의 수를 생성해낼 수 있게 될 것입니다. 그때, $X$의 PDF $f_X(x)$와 $Y$의 PDF $f_Y(y)$ 사이의 관계식이 필요할 것이라는 점이 강의에서 언급됩니다.

이러한 문제에서, 만약 $g$가 일대일대응이면 문제는 상당히 쉬워집니다. 하지만 $g$가 일대일대응 조건을 만족하지 못하는 경우에는 조금 처리해주어야 할 사항들이 있는데, 그 점들이 소개됩니다. 강의에서 나타나는 예는 $g$가 일차함수(affine function, $g(x)=ax+b$)인 경우, 이차함수($g(x)=x^2$)인 경우에 대한 예를 간단히 들고 있습니다. 그리고 일반적인 경우에 대한 설명이 이어집니다.

예를 들어, 이산확률변수 $X$가 세 개의 값 $-1$, $0$, $1$을 가지고

\[\begin{align*} P_X(-1) &=\frac14\\ P_X(0) &=\frac12\\ P_X(1) &=\frac14 \end{align*}\]

와 같이 분포해있다고 가정하겠습니다. 만약 $g(x)=2x-1$와 같은 함수를 생각하면 이 함수로부터 얻어지는 새로운 확률변수 $Y=g(X)=2X-1$은

\[\begin{align*} P_Y(-3) &=\frac14\\ P_Y(-1) &=\frac12\\ P_Y( 1) &=\frac14 \end{align*}\]

와 같은 확률분포를 따르게 됩니다. 하지만 만약 $g(X)=x^2$와 같은 함수를 가정하면, $Y=g(X)=X^2$는

\[\begin{align*} P_Y(0) &=\frac12\\ P_Y(1) &=\frac12 \end{align*}\]

과 같은 확률변수를 따르게 됩니다. 그러니까 $g(x)=2x-1$과 같은 일대일대응 함수의 경우에는 분포가 그대로 유지되지만, $g(x)=x^2$과 같이 일대일조건이 깨지게 되는 경우에는, 기존 분포와는 조금 다른 분포의 모양이 나오게 됩니다.

일반적으로, 이산확률변수 $X$가

\[\begin{align*} P_X(x_1) &=p_1\\ &\vdots\\ P_X(x_n) &=p_n\\ \end{align*}\]

와 같은 분포를 따르고, $g$가 일대일대응이면, 모든 $i=1,2,\cdots,n$에 대하여

\[\begin{align*} P_Y(g(x_i)) &=P(Y=g(x_i))\\ &=P(g(X)=g(x_i))\\ &=P(X=x_i)\\ &=P_X(x_i) \end{align*}\]

입니다. 따라서 $Y$는

\[\begin{align*} P_X\left(g(x_1)\right) &=p_1\\ &\vdots\\ P_X\left(g(x_n)\right) &=p_n\\ \end{align*}\]

와 같은 분포를 따름을 쉽게 알 수 있습니다.

$X$가 연속확률변수인 경우에는 아무리 $g$가 일대일대응이라고 하더라도, $Y$의 분포를 얻는게 쉽지 않습니다. 하지만, 일대일대응 중에서도 단조증가함수 혹은 단조감수함수에 대해서는 비교적 쉽게 결과를 얻을 수 있습니다. 또한, 증가나 감소가 유한 번 일어나는, 비교적 간단한 연속함수의 경우에도 결과를 낼 수 있다는 것이 강의에서 소개되고 있습니다.

함수 $g:\mathbb R\to\mathbb R$이 $$x_1\lt x_2\quad\Longrightarrow\quad g(x_1)\lt g(x_2)$$ 이면 $g$가 단조증가함수(monotonically increasing function)라고 합니다. 만약 $$x_1\lt x_2\quad\Longrightarrow\quad g(x_1)\gt g(x_2)$$ 이면 $g$가 단조감소함수(monotonically increasing function)라고 합니다.
단조증가함수와 단조감수함수를 통틀어서 단조함수(monotonic function)라고 부르기도 합니다. 단조함수가 일대일함수라는 것은 쉽게 증명될 수 있습니다.

(1) 일차함수 $g(x)=ax+b$

확률변수 $X$에 대한 PMF가 $Y=g(X)=aX+b$일 때($a\ne0$), $a\gt0$인 경우와 $a\lt0$인 두 가지의 경우로 나누어볼 수 있습니다. 만약 $a\gt0$이면,

\[\begin{align*} F_Y(y) &=P(Y\le y)\\ &=P(aX+b\le y)\\ &=P\left(X\le\frac{y-b}a\right)\\ &=F_X\left(\frac{y-b}a\right) \end{align*}\]

이므로,

\[\begin{align*} f_Y(y) &=\frac d{dy}F_Y(y)\\ &=\frac d{dy}F_X\left(\frac{y-b}a\right)\\ &=\frac1aF_X'\left(\frac{y-b}a\right)\\ &=\frac1af_X\left(\frac{y-b}a\right)\\ \end{align*}\]

입니다. 반대로, $a\lt0$이면

\[\begin{align*} F_Y(y) &=P(Y\le y)\\ &=P(aX+b\le y)\\ &=P\left(X\ge\frac{y-b}a\right)\\ &=1-F_X\left(\frac{y-b}a\right) \end{align*}\]

이므로,

\[\begin{align*} f_Y(y) &=\frac d{dy}F_Y(y)\\ &=\frac d{dy}\left(1-F_X\left(\frac{y-b}a\right)\right)\\ &=-\frac d{dy}F_X\left(\frac{y-b}a\right)\\ &=-\frac1aF_X'\left(\frac{y-b}a\right)\\ &=-\frac1af_X\left(\frac{y-b}a\right)\\ \end{align*}\]

입니다. 따라서, $a\ne0$을 만족시키는 실수 $a$에 대하여 $Y$의 확률밀도함수 $f_Y(y)$는

\[\begin{aligned} f_Y(y) &= \begin{cases} \frac1af_X\left(\frac{y-b}a\right) &(a\gt0)\\ -\frac1af_X\left(\frac{y-b}a\right) &(a\lt0)\\ \end{cases}\\[10pt] &=\frac{f_X\left(\frac{y-b}a\right)}{|a|} \end{aligned}\tag{$\ast$}\]

로 계산됩니다.

예를 들어, $Y=\frac12X+1$인 경우 $\left(a=\frac12\right)$

\[P(1\lt X\le 2)=P\left(\frac32\lt X\le 2\right)\]

입니다. 그러니까, $X$의 입장에서 $1$의 길이를 가지는 구간에 대한 확률과 $Y$의 입장에서 $\frac12$의 길이를 가지는 구간에 대한 확률이 같습니다. 그러면, 밀도함수의 기준에서 봤을 때는 $f_X$에 비해 $f_Y$의 밀도가 두 배 더 높을 것입니다. 실제로 $a=\frac12$이면, 서로 대응되는 부분에서의 $f_Y$의 값이 $f_X$의 값의 두 배가 되는 것이 $(\ast)$에 나타나있습니다.

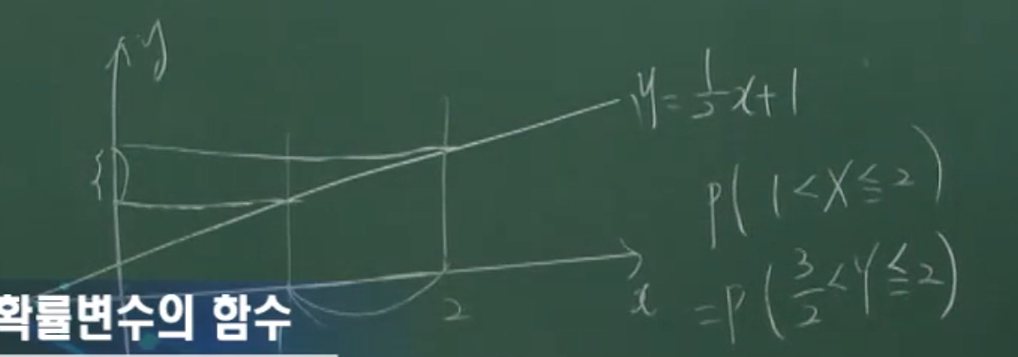
(2) 이차함수 $g(x)=x^2$

마찬가지로 $Y=g(X)=X^2$에 대하여 해보겠습니다. 양수 $y$에 대하여

\[\begin{align*} F_Y(y) &=P(Y\le y)\\ &=P(X^2\le y)\\ &=P(-\sqrt y\le X\le\sqrt y)\\ &=F_X(\sqrt y)-F_X(-\sqrt y) \end{align*}\]

이면,

\[\begin{aligned} f_Y(y) &=\frac d{dy}F_Y(y)\\ &=\frac d{dy}\left(F_X(\sqrt y)-F_X(-\sqrt y)\right)\\ &=\frac{f_X(\sqrt y)}{2\sqrt y}+\frac{f_X(-\sqrt y)}{2\sqrt y} \end{aligned}\tag{$\ast\ast$}\]

이 됩니다.

예를 들어 $X$가 exponential distribution을 따르면

\[f_X(x)=\lambda e^{-\lambda x}\qquad(x\ge0)\]

$Y=X^2$은

\[\begin{align*} f_Y(y) &=\frac{f_X(\sqrt y)}{2\sqrt y}+\frac{f_X(-\sqrt y)}{2\sqrt y}\\ &=\frac{\lambda e^{-\lambda\sqrt y}}{2\sqrt y}+\frac{\lambda e^{\lambda\sqrt y}}{2\sqrt y} \end{align*}\]

의 분포를 따릅니다.

$g(x)=ax+b$는 일대일함수였고, 따라서 하나의 $y$에 대하여, $y=g(x)$를 만족시키는 단 하나의 $x=g^{-1}(y)=\frac{y-b}a$가 존재했습니다. 즉, $y$의 inverse image인 $g^{-1}\left({x}\right)$가 하나의 원소를 가졌습니다;

\[g^{-1}\left(\{x\}\right)=\left\{\frac{y-b}a\right\}\]

반면, $g(x)=x^2$는 일대일함수 조건을 만족하지 못합니다. 하나의 $y$에 대하여 $y=g(x)$를 만족시키는 $x$는 두 개 $x=\sqrt y$, $x=-\sqrt y$ 존재합니다. 다시 말해,

\[g^{-1}\left(\{x\}\right)=\{-\sqrt y,\sqrt y\}\]

입니다. 그런 이유로 $(\ast\ast)$의 식에서는 두 개의 항이 나왔습니다.

(3) 일반적인 함수

다음으로, 강의에서는 일반적인 경우를 다룹니다. 만약 어떤 함수 $g:\mathbb R\to\mathbb R$가 연속함수이고 미분가능하며, 극값의 개수가 유한하고, 실수 $y$가 $g$의 극값이 아니라고 가정하면, $g$의 함수의 그래프는 다음과 같이 생겼습니다.

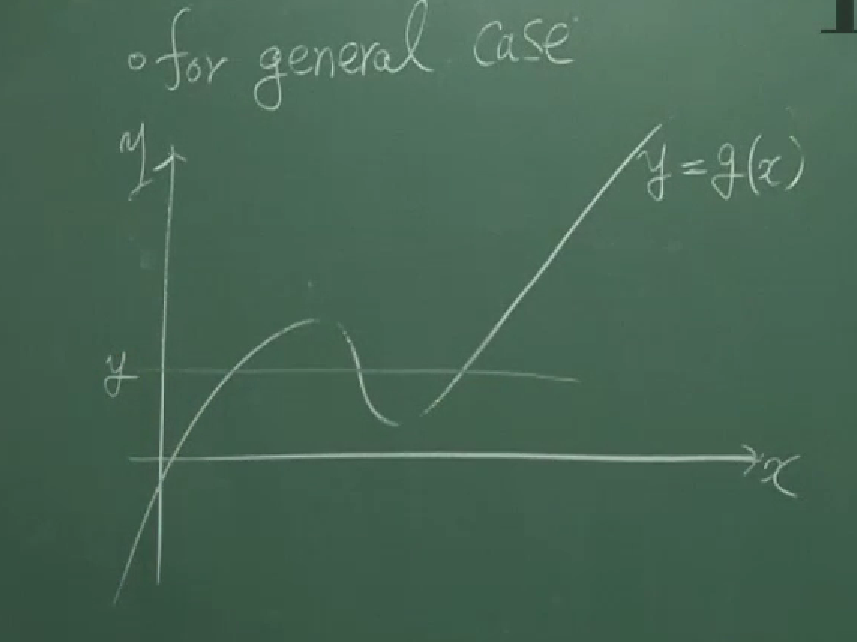
즉, $y=f(x)$를 만족하는 $x$의 값이 세 개인 경우를 다룹니다. 이것들을 각각 $x_1$, $x_2$, $x_3$라고 하면,

\[f^{-1}\left(\{y\}\right)=\{x_1,x_2,x_3\}\]

입니다. 위와 같은 특정한 경우에 $Y$의 CDF는

\[\begin{align*} F_Y(y) &=P(Y\le y)\\ &=P(X\le x_1)+P(x_2\lt X\le x_3)\\ &=F_X(x_1)-F_X(x_2)+F_x(x_3) \end{align*}\]

입니다. 이것을 $y$에 대해 미분하여 $f_Y(y)$를 구하면

\[\begin{align*} f_Y(y) &=\frac d{dy}F_Y(y)\\[10pt] &=\frac d{dy}\left(F_X(x_1)-F_X(x_2)+F_x(x_3)\right)\\[10pt] &=\frac d{dy}F_X(x_1)-\frac d{dy}F_X(x_2)+\frac d{dy}F_X(x_3)\\[10pt] &=\left[\frac d{dy}F_X(x)\right]_{x=x_1}-\left[\frac d{dy}F_X(x)\right]_{x=x_2}+\left[\frac d{dy}F_X(x)\right]_{x=x_3}\\[10pt] &=\left[\frac{dx}{dy}\cdot\frac d{dx}F_X(x)\right]_{x=x_1}-\left[\frac{dx}{dy}\cdot\frac d{dx}F_X(x)\right]_{x=x_2}+\left[\frac{dx}{dy}\cdot\frac d{dx}F_X(x)\right]_{x=x_3}\\[10pt] &=\left[\frac{\frac d{dx}F_X(x)}{\frac{dy}{dx}}\right]_{x=x_1}-\left[\frac{\frac d{dx}F_X(x)}{\frac{dy}{dx}}\right]_{x=x_2}+\left[\frac{\frac d{dx}F_X(x)}{\frac{dy}{dx}}\right]_{x=x_3}\\[10pt] &=\left[\frac{f_X(x)}{g'(x)}\right]_{x=x_1}-\left[\frac{f_X(x)}{g'(x)}\right]_{x=x_2}+\left[\frac{f_X(x)}{g'(x)}\right]_{x=x_3}\\[10pt] &=\frac{f_X(x_1)}{g'(x_1)}-\frac{f_X(x_2)}{g'(x_2)}+\frac{f_X(x_3)}{g'(x_3)}\\[10pt] &=\sum_{i=1}^3\frac{f_X(x_i)}{|g'(x_i)|} \end{align*}\]

일반적으로 실수 $y$에 대하여 $y=g(x)$를 만족하는 $x$의 값이 $x_1$, $x_2$, $\cdots$, $x_n$일 때, $Y$의 PDF $f_Y(y)$는

\[f_Y(y)=\sum_{i=1}^n\frac{f_X(x_i)}{|g'(x_i)|}\]

입니다. 여기에 $g(x)=ax+b$를 대입해보면 $n=1$이고, $x_1=\frac{y-b}a$이므로,

\[\begin{align*} f_Y(y) &=\sum_{i=1}^1\frac{f_X(x_1)}{|g'(x_1)|}\\[10pt] &=\frac{f_X(x_1)}{|g'(x_1)|}\\[10pt] &=\frac{f_X\left(\frac{y-b}a\right)}{|a|} \end{align*}\]

가 되어 $(\ast)$와 일치합니다. 이번에는 $g(x)=x^2$을 대입해보면 $n=2$이고,$x_1=-\sqrt y$, $x_2=\sqrt y$이므로,

\[\begin{align*} f_Y(y) &=\sum_{i=1}^2\frac{f_X(x_1)}{|g'(x_1)|}\\[10pt] &=\frac{f_X(x_1)}{|g'(x_1)|}+\frac{f_X(x_2)}{|g'(x_2)|}\\[10pt] &=\frac{f_X(x_1)}{|2x_1|}+\frac{f_X(x_2)}{|2x_2|}\\[10pt] &=\frac{f_X(-\sqrt y)}{|-2\sqrt y|}+\frac{f_X(\sqrt y)}{|2\sqrt y|}\\[10pt] &=\frac{f_X(-\sqrt y)}{2\sqrt y}+\frac{f_X(\sqrt y)}{2\sqrt y} \end{align*}\]

가 되어 $(\ast\ast)$와 일치합니다.

ex.6.2

$X\sim N(0,1)$이고, $Y=X^2$일 때, $Y$의 분포를 알아보겠습니다. $X$의 PDF는

\[f_X(x)=\frac1{\sqrt{2\pi}}e^{-\frac{x^2}2}\]

로 주어지므로, $(\ast\ast)$를 적용하면, 임의의 양수 $y$에 대하여

\[\begin{align*} f_Y(y) &=\frac{f_X(\sqrt y)}{2\sqrt y}+\frac{f_X(-\sqrt y)}{2\sqrt y}\\ &=\frac1{2\sqrt{2\pi y}}e^{-\frac y2}+\frac1{2\sqrt{2\pi y}}e^{-\frac y2}\\ &=\frac1{\sqrt{2\pi y}}e^{-\frac y2} \end{align*}\]

6.3 Expectations

여기에서, $\langle05\rangle$에서 미뤄두었던 LOTUS(law of the unconscious statistician)가 나옵니다.

\[\begin{align*} E[g(X)]&=\sum_ig(x_i)P_X(x_i) &&(\text{discrete})\\ E[g(X)]&=\int_{-\infty}^\infty g(x)f_X(x)\,dx &&(\text{continuous}) \end{align*}\tag{LOTUS}\]

discrete case에 대하여 간단하게 증명해보겠습니다. 확률변수 $X$가 $x_1$, $\cdots$, $x_m$을 값으로 가지고, $Y=g(X)$가 $y_1$, $\cdots$, $y_n$을 값으로 가진다면 $g^{-1}(y_1)$, $g^{-1}(y_2)$, $\cdots$, $g^{-1}(y_n)$은 $\{x_1,x_2,\cdots,x_m\}$의 partition이 됩니다($\star$). 이때, $g^{-1}(y_j)$는

\[g^{-1}(y_j)=\{x_i:g(x_i)=y_j\}\]

인 $x_i$들의 집합을 말합니다. 따라서,

\[\begin{align*} E\left[g(X)\right] &=\sum_{j=1}^ny_jP(Y=y_j)\\ &=\sum_{j=1}^ny_jP(g(X)=y_j)\\ &=\sum_{j=1}^ny_jP\left(X\in g^{-1}\left(\{y_j\}\right)\right)\\ &=\sum_{j=1}^ny_j\sum_{x_i\in g^{-1}\left(\{y_j\}\right)}P(X=x_i)\\ &=\sum_{j=1}^n\sum_{x_i\in g^{-1}\left(\{y_j\}\right)}g(x_i)P(X=x_i)\\ &\stackrel\star=\sum_{i=1}^mg(x_i)P(X=x_i) \end{align*}\]

입니다. 따라서 discrete case의 LOTUS가 성립합니다.$\square$

다음으로, continuous case입니다. 일반적인 continuous case에 대한 증명은 어렵습니다. 이 포스트에서는 $g$가 단조함수이면서 미분가능하며, 모든 $x$에 대하여 $g’(x)\ne0$인 경우만을 다루겠습니다.

만약, $g$가 단조증가함수이면 $f_X(x)$와 $f_Y$ 사이의 관계식은

\[\begin{align*} F_Y(y) &=P(Y\le y)\\ &=P(g(X)\le y)\\ &\stackrel{\star\star}=P(X\le g^{-1}(y))\\ &=F_X\left(g^{-1}(y)\right)\\ f_Y(y) &=\frac d{dy}F_Y(y)\\ &=\frac{d g^{-1}(y)}{dy}F_X'\left(g^{-1}(y)\right)\\ &=\frac{f_X\left(g^{-1}(y)\right)}{g'(g^{-1}(y))} \end{align*}\]

입니다. $\star\star$에서 $g$가 단조증가함수인 것이 사용되었습니다. 따라서

\[\begin{align*} E[g(X)] &=E[Y]\\[10pt] &=\int_{y=-\infty}^{y=\infty}yf_Y(y)\,dy\\[10pt] &=\int_{y=-\infty}^{y=\infty}y\frac{f_X\left(g^{-1}(y)\right)}{g'(g^{-1}(y))}\,dy\\[10pt] &=\int_{x=-\infty}^{x=\infty}g(x)\frac{f_X(x)}{g'(x)}\frac{dy}{dx}\,dx\\[10pt] &=\int_{x=-\infty}^{x=\infty}g(x)f_X(x)\,dx\\ \end{align*}\]

입니다. 반대로, $g$가 단조감소함수이면

\[\begin{align*} F_Y(y) &=P(Y\le y)\\ &=P(g(X)\le y)\\ &\stackrel{\star\star\star}=P(X\ge g^{-1}(y))\\ &=1-F_X\left(g^{-1}(y)\right)\\ f_Y(y) &=\frac d{dy}\left(1-F_X\left(g^{-1}(y)\right)\right)\\ &=-\frac{d g^{-1}(y)}{dy}F_X'\left(g^{-1}(y)\right)\\ &=-\frac{f_X\left(g^{-1}(y)\right)}{g'(g^{-1}(y))} \end{align*}\]

입니다. $\star\star\star$에서 $g$가 단조감소함수인 것이 사용되었습니다. 따라서

\[\begin{align*} E[g(X)] &=E[Y]\\[10pt] &=\int_{y=-\infty}^{y=\infty}yf_Y(y)\,dy\\[10pt] &=-\int_{y=-\infty}^{y=\infty}y\frac{f_X\left(g^{-1}(y)\right)}{g'(g^{-1}(y))}\,dy\\[10pt] &=-\int_{x=\infty}^{x=-\infty}g(x)\frac{f_X(x)}{g'(x)}\frac{dy}{dx}\,dx\\[10pt] &=\int_{x=-\infty}^{x=\infty}g(x)f_X(x)\,dx\\ \end{align*}\]

입니다.

따라서 continuous case의 LOTUS가 성립합니다.$\square$

15 연속확률변수의 합과 컨볼루션

이전 강의에서 두 확률변수 $X$, $Y$ 사이에 $Y=g(X)$인 함수 $g:\mathbb R\to\mathbb R$이 존재할 때, $f_X(x)$를 통해 $f_Y(y)$를 구하는 방법에 대해 다뤘습니다. 그러니까 $g$는 일변수의 실함수였습니다.

조금 더 일반적인 상황에서는, 함수 $g$는 multivariate function(다변수함수)일 수도 있고 ($g:\mathbb R^m\to\mathbb R$), vector valued function(벡터함수)일 수도 있으며($g:\mathbb R\to\mathbb R^n$), 둘 다일 수도 있습니다($g:\mathbb R^m\to\mathbb R^n$). 이번 강의에서는 $g$가 multivariate function인 경우

\[g:\mathbb R^m\to\mathbb R\]

에 대해 다룹니다. 그 중에서도 가장 간단한 $m=2$인 경우로부터 시작하고 있습니다. 즉

\[g:\mathbb R^2\to\mathbb R\]

인, $g$가 이변수함수(bivariate function)인 경우입니다. 기존에 주어진 연속확률변수 $X$, $Y$를 가지고, 새로운 연속확률변수 $S=g(X,Y)$가 주어지는 경우입니다.

$X$와 $Y$의 확률함수가 주어져있는 경우에, 새로운 확률변수 $S$의 CDF를 구하는 방법은

\[\begin{align*} F_S(s) &=P(S\le s)\\ &=P(g(X,Y)\le s)\\ &=\iint_{g(x,y)\le s}F_{XY}(x,y)\,dx\,dy \end{align*}\]

인 것은 당연합니다. 그리고, $S$의 PDF는 위 식을 미분하면 얻어집니다;

\[f_S(s)=\frac d{ds}\iint_{g(x,y)\le s}F_{XY}(x,y)\,dx\,dy\]

그러니까, 위의 두 식은 항상 성립하는 식입니다.

convolution

모든 종류의 이변수 함수(bivariate function) 중에서 가장 간단하면서도 중요한 경우는 $g$가

\[g(x,y)=x+y\]

로 주어지는 경우입니다. 다시 말해, 두 확률변수 $X$, $Y$에 대하여 새로운 확률변수 $X+Y$의 분포를 구해보는 것입니다. 이 새로운 확률변수 $S=X+Y$의 PDF는

\[f_S(s)=\int_{-\infty}^\infty f_{XY}(s-u,u)\,du \tag{$\ast$}\]

로 주어집니다. 당연히, 위의 식에서 $u$는 dummy variable입니다. 그러니까, 위의 식에서 $u$말고 다른 어떤 변수로 넣어도, 상관없습니다. 만약, $X$와 $Y$가 독립이면

\[f_S(s)=\int_{-\infty}^\infty f_X(s-u)f_Y(u)\,du \tag{$\ast\ast$}\]

와 같이 쓸 수도 있습니다. $(\ast\ast)$에 대한 증명을 강의에서는 다음과 같이 하고 있습니다.

\[\begin{align*} F_S(s) &=P(S\le s)\\ &=\iint_{x+y\le s}f_{XY}(x,y)\,dx\,dy \end{align*}\]

에서 $x+y\le s$인 부등식의 영역은

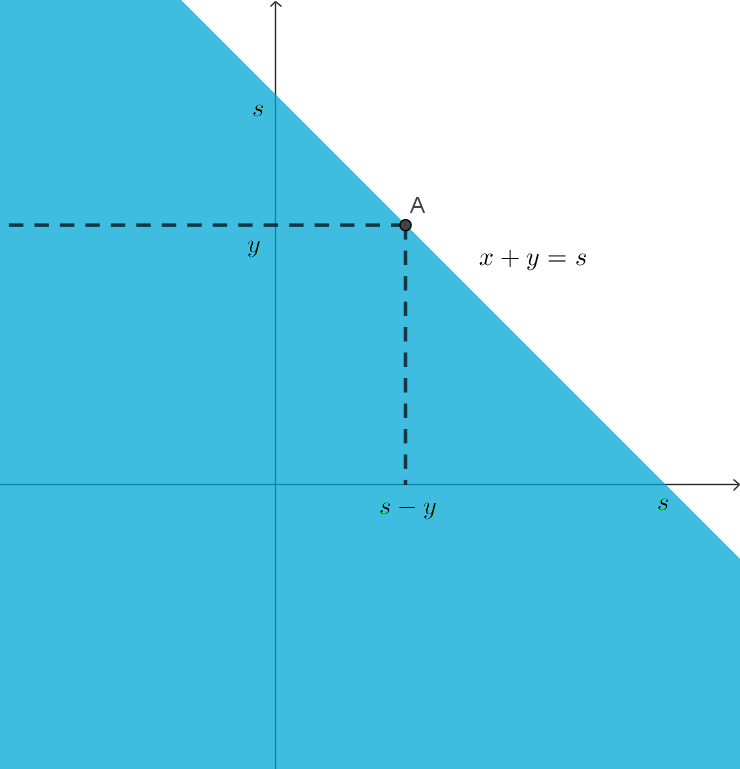
와 같이 주어집니다. 이 이중적분에서, $y$는 $-\infty$부터 $\infty$까지 움직이고, $y$가 하나의 특정한 값으로 고정되었을 때, $x$는 $-\infty$부터 $s-y$까지 움직이므로

\[\begin{align*} F_S(s) &=\int_{-\infty}^\infty\int_{-\infty}^{s-y}f_{XY}(x,y)\,dx\,dy\\ &=\int_{-\infty}^\infty\int_{-\infty}^{s-y}f_X(x)f_Y(y)\,dx\,dy\\ &=\int_{-\infty}^\infty f_Y(y)\int_{-\infty}^{s-y}f_X(x)\,dx\,dy\\ &=\int_{-\infty}^\infty f_Y(y)F_X(s-y)\,dy \end{align*}\]

양변을 $s$에 대해 미분하면

\[\begin{align*} f_S(s) &=\frac d{ds}\int_{-\infty}^\infty f_Y(y)F_X(s-y)\,dy\\ &\stackrel\star=\int_{-\infty}^\infty\frac d{ds}f_Y(y)F_X(s-y)\,dy\\ &=\int_{-\infty}^\infty f_Y(y)f_X(s-y)\,dy \end{align*}\]

이 된다는 것입니다. 따라서 $(\ast\ast)$가 성립합니다.

이 증명도 맞는 증명이겠지만, $\star$의 과정에서 미분과 적분의 순서를 바꾼 것에 대한 이유를 충분히 찾지 못하겠어서, 다른 증명을 찾아봤습니다. DeGroot의 책에는 다음과 같이 증명하고 있습니다.

\[F_S(s)=\int_{-\infty}^\infty\int_{-\infty}^{s-y}f_{XY}(x,y)\,dx\,dy\]

에서 $x+y=t$로 치환하면 $x=t-y$, $dx=dt$, $x=-\infty\iff t=-\infty$, $x=s-y\iff t=s$ 이므로

\[\begin{align*} F_S(s) &=\int_{-\infty}^\infty\int_{-\infty}^sf_{XY}(t-y,y)\,dt\,dy\\ \end{align*}\]

입니다. 이 과정에서 적분영역은 $x\le s$이고,

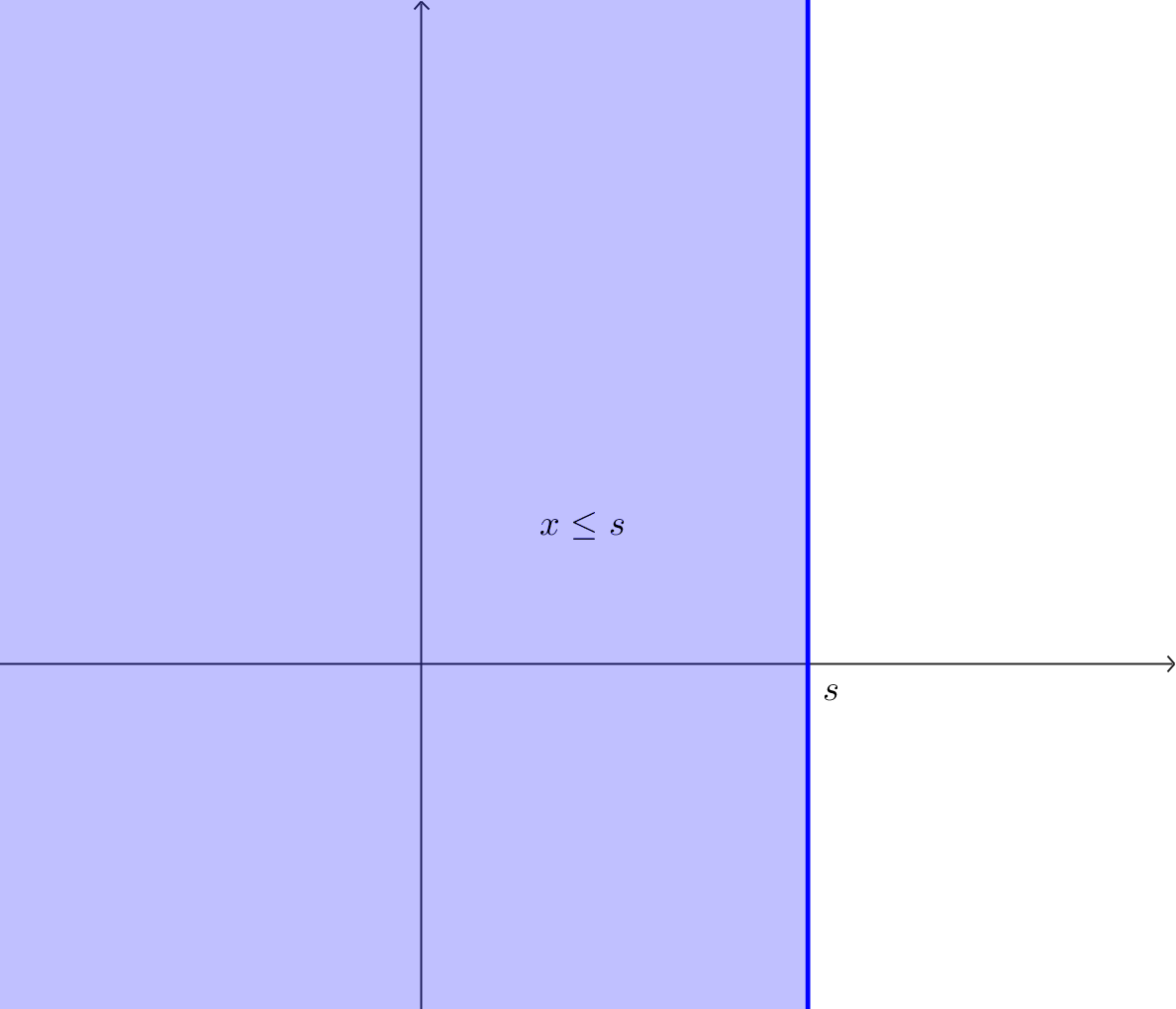
따라서 적분의 순서를 바꿀 수 있습니다.

\[\begin{align*} F_S(s) &=\int_{-\infty}^s\int_{-\infty}^\infty f_{XY}(t-y,y)\,dy\,dt\\ \end{align*}\]

양변을 미분하면

\[f_S(s)=\int_{-\infty}^\infty f_{XY}(s-y,y)\,dy\]

이고, 따라서 $(\ast)$가 성립하며, $(\ast\ast)$도 성립합니다.

정의 : convolution (continuous)
일반적으로, 두 함수 $f:\mathbb R\to\mathbb R$, $g:\mathbb R\to\mathbb R$에 대하여 새로운 함수 $f\ast g:\mathbb R\to\mathbb R$을 $$(f\ast g)(s)=\int_{-\infty}^\infty f(u)g(s-u)\,du$$ 로 정의할 때, $f\ast g$는 $f$와 $g$의 convolution이라고 불립니다.

따라서, 앞서의 결과를 정리하면, 두 연속확률변수 $X$와 $Y$에 대하여 $S=X+Y$의 확률밀도함수 $f_S$는 $f_X$와 $f_Y$의 convolution입니다. 다시 말해,

\[f_S=f_X\ast f_Y\]

라고 쓸 수 있고, $f_S(s)$는

\[f_S(s)=\int_{-\infty}^\infty f(u)g(s-u)\,du\]

를 만족시키는 함수입니다.

강의에는 포함되어 있지 않지만, convolution 연산 $\ast$의 기본적인 성질들에 대해 더 적어보려 합니다. $\ast$은 교환법칙과 결합법칙이 성립합니다. 먼저, $\ast$가 교환법칙이 성립한다는 것은, $f\ast g=g\ast f$가 성립한다는 것입니다. 왜냐하면

\[\begin{align*} (f\ast g)(s) &=\int_{-\infty}^\infty f(t)g(s-t)\,dt\\ &=-\int^{-\infty}_\infty f(s-u)g(u)\,du\\ &=\int_{-\infty}^\infty g(u)f(s-u)\,du\\ &=(g\ast f)(s) \end{align*}\]

이기 때문입니다. 또한, 결합법칙도 성립합니다. 왜냐하면 (적분기호의 위끝과 아래끝을 생략했습니다.)

\[\begin{align*} ((f\ast g)\ast h)(s) &=(h\ast(f\ast g))(s)\\ &=\int_{-\infty}^\infty (f\ast g)(s-t)h(t)\,dt\\ &=\int_{-\infty}^\infty\int_{-\infty}^\infty f(u)g(s-t-u)\,du\,h(t)\,dt\\ &=\int_{-\infty}^\infty f(u)\int_{-\infty}^\infty h(t)g(s-u-t)\,dt\,du\\ &=\int_{-\infty}^\infty f(u)(h\ast g)(s-u)\,du\\ &=\int_{-\infty}^\infty f(u)(g\ast h)(s-u)\,du\\ &=(f\ast(g\ast h))(s) \end{align*}\]

이기 때문입니다. 따라서, 실수 전체에서 적분가능한 함수들의 집합을 $\mathcal F$이라고 하면, $(\mathcal F,\ast)$는 abelian group입니다.

다시 강의로 돌아오겠습니다. 강의에서는 convolution에 대한 개념정리를 다음과 같이 하고 있습니다(표현을 조금 바꾸어서 적었습니다.).

$x(t)\ast h(t)=y(t)$

1. Select functions $x(t)$ and $h(t)$, transform $h(t)$ symmetrically about $t=0$ to get $x(t)$ and $h(-t)$.
2. Shift the symmetrically transformed function $h(-t)$ by $s$ to get $x(t)$ and $h(s-t)$.
3. Product the overlapped region of $y=x(t)$ and $y=h(s-t)$ by calculating

\[\int_{-\infty}^\infty x(t)h(s-t)\,ds\]

ex.6.3

convolution에 대한 예시로서, 두 함수 $x(u)$와 $h(u)$가

\[\begin{align*} x(u)&= \begin{cases} 1&(0\le u\le 1)\\ 0&(\text{otherwise}) \end{cases}\\[10pt] h(u)&= \begin{cases} \frac12&(0\le u\le2)\\ 0&(\text{otherwise}) \end{cases} \end{align*}\]

와 같이 주어지는 경우입니다. 그러면 실수 $t$에 대하여, $y=x(u)$와 $y=h(t-u)$의 그래프는 아래와 같이 주어집니다.

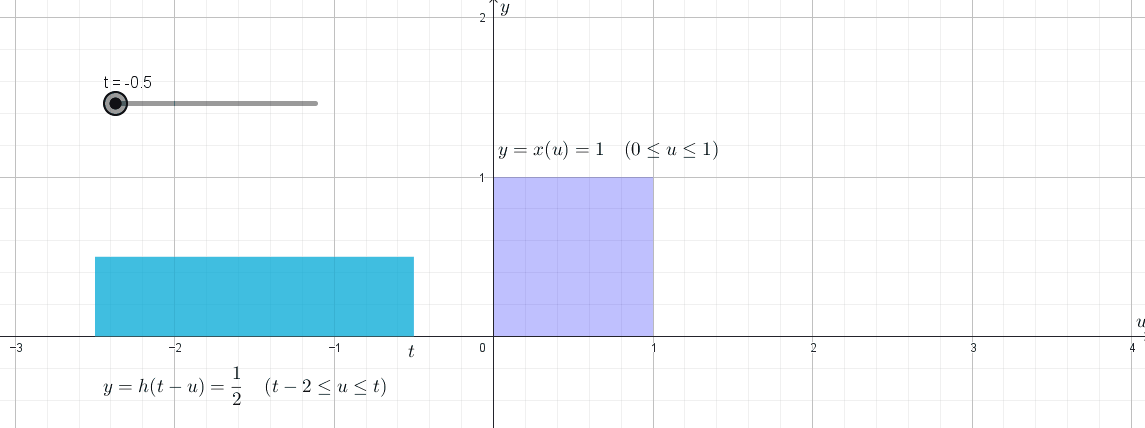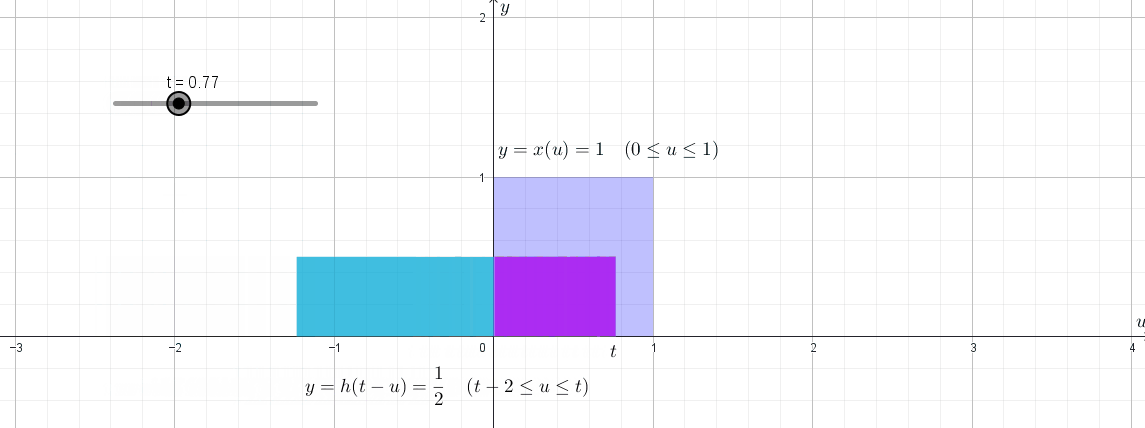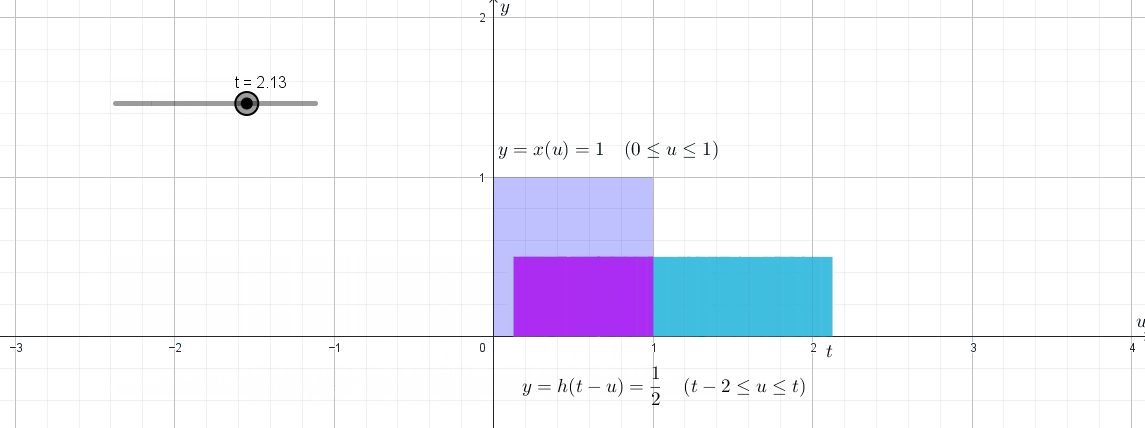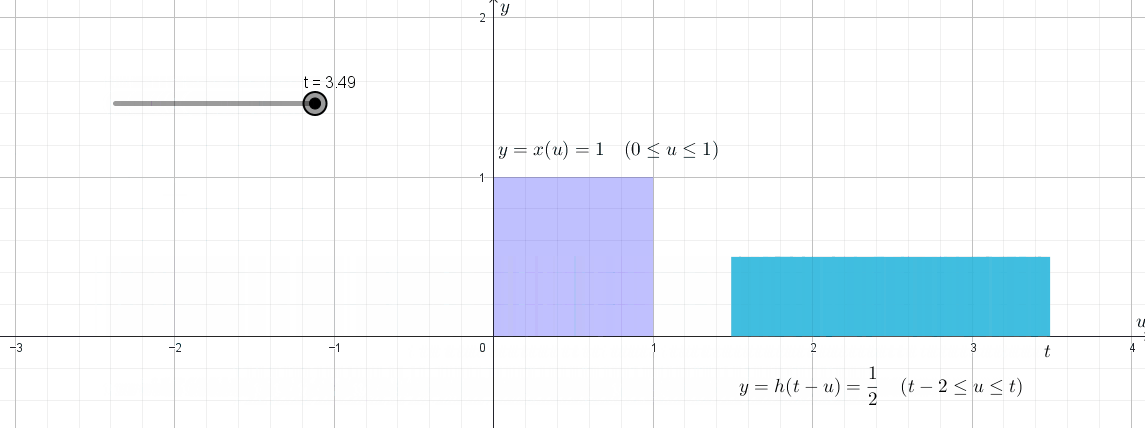
$x(u)$가 0이 아닌 $u$들의 집합을 $\text{supp}(x)$라고 하고, $h(t-u)$가 0이 아닌 집합을 $\text{supp}(h)$라고 하면,

\[\begin{align*} \text{supp}(x) &=\{u:0\le u\le1\}\\ &=[0,1]\\ \text{supp}(h) &=\{u:0\le t-u\le 2\}\\ &=\{u:t-2\le u\le t\}\\ &=[t-2,t] \end{align*}\]

이고, 따라서

\[\begin{matrix} &\text{supp}(x)\cap\text{supp}(h)&x(t)h(t-u)&(x\ast h)(t)\\[10pt] t\le 0 &\varnothing & &0 \\[10pt] 0\le t\le1 &[0,t] &\frac12 &\frac12t \\[10pt] 1\le t\le2 &[1,2] &\frac12 &\frac12 \\[10pt] 2\le t\le3 &[t-2,1] &\frac12 &\frac12(3-t)\\[10pt] t\ge0 &\varnothing & &0 \\ \end{matrix}\]

입니다. $y=\left(x\ast h\right)(t)$의 그래프를 그려보면

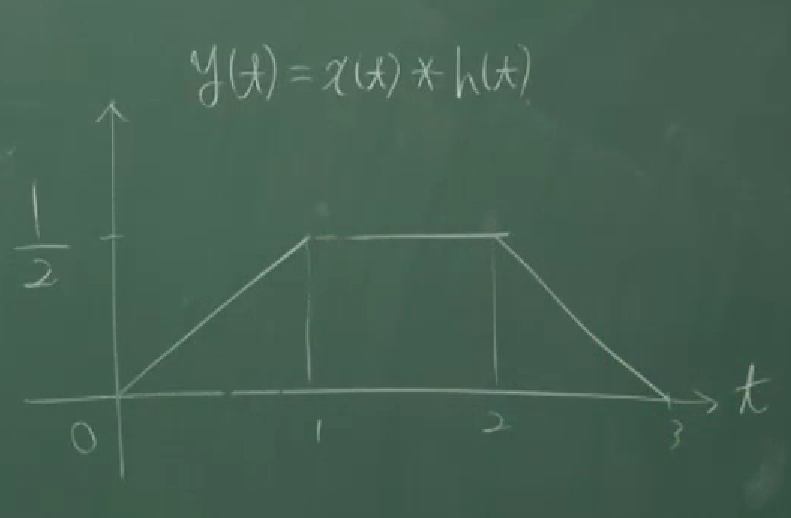
와 같이 됩니다.

ex.6.5. Erlang distribution

convolution을 사용하면 $\langle08\rangle$에서 미뤄두었던 Erlang distribution에 대한 PDF 식을 유도할 수 있습니다. 다시 복습해보면, 사건의 평균 발생주기가 $\lambda$인 Poisson process에서 사건이 시각 $T_0$, $T_1$, $T_2$에 일어났다고 가정하면, $T_1-T_0$과 $T_2-T_1$는 exponential distribution을 따릅니다. $X=T_1-T_0$, $Y=T_2-T_1$라고 두면,

\[\begin{align*} f_X(x)&= \begin{cases} \lambda e^{-\lambda x} &x\ge0\\ 0 &(\text{otherwise}) \end{cases}\\[20pt] f_Y(y)&= \begin{cases} \lambda e^{-\lambda y} &y\ge0\\ 0 &(\text{otherwise}) \end{cases} \end{align*}\]

입니다. 이때, $T_3-T_1$는 Erlang-$2$ distribution을 따른다고 할 수 있습니다. 확률변수 $S$를 $S=T_3-T_1=X+Y$라고 두면 Erlang-$k$ distribution의 식

\[f_X(x)=\frac{\lambda^kx^{k-1}}{(k-1)!}e^{-\lambda x}\qquad x\ge0 \tag{$\ast\ast\ast$}\]

에 $k=2$를 대입한

\[f_S(s)=\lambda^2se^{-\lambda s}\qquad s\ge0\]

와 같은 식이 유도되어야 합니다. 실제로 convolution을 통해 식을 유도해보기 전에, 두 함수 $f_X(u)$와 $f_Y(s-u)$가 0이 되지 않는 구간 (두 함수 $f_X(u)$와 $f_Y(s-u)$의 support)을 계산해보면

\[\begin{align*} \text{supp}(f_x(u)) &=\{u:f_X(u)\gt0\}\\ &=\{u:u\gt0\}\\ \text{supp}(f_Y(s-u)) &=\{u:f_Y(s-u)\gt0\}\\ &=\{u:s-u\gt0\}\\ &=\{u:u\lt s\} \end{align*}\]

입니다. (일반적으로 함수 $f$의 support는 $f(x)\ne0$인 $x$들의 집합에 closure를 취한 것이지만, 여기에서는 closure를 취하지 않은 버전의 support를 구했습니다.) 따라서, 두 함수의 곱 $f_X(u)f_Y(s-u)$은 $s\gt0$일 때, 0이 아닌 구간 $0\lt u\lt s$을 가지지만, 그렇지 않은 경우에는 모든 실수 $u$에 대하여 $f_X(u)f_Y(s-u)=0$입니다. 그러므로,

\[\begin{aligned} (f_X\ast f_Y)(s) &=\int_{-\infty}^\infty f_X(u)f_Y(s-u)\,du\\ &=\int_0^sf_X(u)f_Y(s-u)\,du\\ &=\int_0^s\lambda e^{-\lambda u}\times\lambda e^{-\lambda(s-u)}\,du\\ &=\lambda^2\int_0^se^{-\lambda s}\,du\\ &=\lambda^2se^{-\lambda s} \end{aligned}\qquad(s\ge0)\]

이 되어, Erlang-$2$ PDF의 식과 일치합니다.

일반적인 Erlang-$k$ distribution의 PDF 식을 유도하기 위해 다시, 사건의 평균 발생주기가 $\lambda$인 Poisson process에서 사건이 시각 $T_1$, $T_2$, $\cdots$, $T_k$에 일어났다고 가정하겠습니다. 그리고, $X_i=X_i-X_{i-1}$로 두면 ($i=1,2,\cdots,k$)

\[f_{X_i}(x_i)= \begin{cases} \lambda e^{-\lambda x_i} &x_i\ge0\\ 0 &(\text{otherwise}) \end{cases}\]

입니다. 아까, convolution 연산 $\ast$가 결합법칙을 만족한다고 했으므로, 새로운 확률변수 $S=X_1+\cdots+X_k$에 대하여

\[f_S=f_{X_1}\ast f_{X_2}\ast\cdots\ast f_{X_k}\]

는 잘 정의된 함수입니다.

$k=1$, $k=2$일 때에는 이미 $(\ast\ast\ast)$이 성립함을 확인했습니다. $k-1$의 경우에 $(\ast\ast\ast)$이 성립한다고 가정하고, $k$인 경우를 보겠습니다. $X=T_1-T_0$, $Y=T_k-T_1$이라고 하면, 이미

\[\begin{align*} f_X(x)&= \begin{cases} \lambda e^{-\lambda x} &x\ge0\\ 0 &(\text{otherwise}) \end{cases}\\[20pt] f_Y(y)&= \begin{cases} \frac{\lambda^{k-1}y^{k-2}}{(k-2)!}e^{-\lambda y} &y\ge0\\ 0 &(\text{otherwise}) \end{cases} \end{align*}\]

를 알고 있는 셈입니다. 이때, $S=T_k-T_0=X+Y$로 나타낼 수 있는 새로운 확률변수 $S$가 $(\ast\ast\ast)$를 만족시키는지 확인하려고 합니다. convolution으로 $f_S$를 계산해보면, $s\ge0$일 때

\[\begin{align*} f_S(s) &=\left(f_{X_1}\ast \left(f_{X_2}\ast\cdots\ast f_{X_k}\right)\right)(s)\\ &=(f_X\ast f_Y)(s)\\ &=(f_X\ast f_Y)(s)\\ &=\int_{-\infty}^\infty\lambda e^{-\lambda u}\times\frac{\lambda^{k-1}(s-u)^{k-2}}{(k-2)!}e^{-\lambda(s-u)}\,du\\ &=\int_0^s\lambda e^{-\lambda u}\times\frac{\lambda^{k-1}(s-u)^{k-2}}{(k-2)!}e^{-\lambda(s-u)}\,du\\ &=\frac{\lambda^k}{(k-2)!}\int_0^se^{-\lambda s}(s-u)^{k-2}\,du\\ &=\frac{\lambda^ke^{-\lambda s}}{(k-2)!}\int_s^0v^{k-2}\times(-1)\,dv\\ &=\frac{\lambda^ke^{-\lambda s}}{(k-2)!}\int_0^sv^{k-2}\,dv\\ &=\frac{\lambda^ke^{-\lambda s}}{(k-2)!}\times\frac{s^{k-1}}{k-1}\\ &=\frac{\lambda^ks^{k-1}}{(k-1)!}e^{-\lambda s} \end{align*}\]

이 되어 정말로 $(\ast\ast\ast)$가 성립합니다. 따라서, Erlang-$k$ distribution의 PDF 식이 증명되었습니다.

moments of sum of random variables

두 확률변수 $X$, $Y$의 합 $S=X+Y$의 평균은 각 확률변수의 합과 같습니다 ;

\[E[X+Y]=E[X]+E[Y]\]

연속확률변수의 경우에만 증명해보면

\[\begin{align*} E[X+Y] &=\iint_{\mathbb R^2}(x+y)f_{XY}(x,y)\,dx\,dy\\ &=\iint_{\mathbb R^2}xf_{XY}(x,y)\,dx\,dy+\iint_{\mathbb R^2}yf_{XY}(x,y)\,dx\,dy\\ &=\int_{\mathbb R}x\int_{\mathbb R}f_{XY}(x,y)\,dy\,dx +\int_{\mathbb R}y\int_{\mathbb R}f_{XY}(x,y)\,dx\,dy\\ &=\int_{\mathbb R}xf_X(x)\,dx+\int_{\mathbb R}yf_Y(y)\,dy\\ &=E[X]+E[Y] \end{align*}\]

가 됩니다. 이산확률변수의 경우에도 비슷하게 증명할 수 있습니다.

$S=X+Y$의 분산은

\[\begin{align*} {\sigma_S}^2 &=E\left[\left\{(X+Y)-(E[X]+E[Y])\right\}^2\right]\\ &=E\left[\left\{(X+Y)-(\mu_X+\mu_Y)\right\}^2\right]\\ &=E\left[\left\{(X-\mu_X)+(Y-\mu_Y)\right\}^2\right]\\ &=E\left[(X-\mu_X)^2+2(X-\mu_X)(Y-\mu_Y)+(Y-\mu_Y)^2\right]\\ &=E\left[(X-\mu_X)^2\right] +2E\left[(X-\mu_X)(Y-\mu_Y)\right] +E\left[(Y-\mu_Y)^2\right]\\ &={\sigma_X}^2+2\text{cov}(X,Y)+{\sigma_Y}^2 \end{align*}\]

로 계산될 수 있습니다. 만약, $X$와 $Y$가 uncorrelated이면,

\[{\sigma_S}^2={\sigma_X}^2+{\sigma_Y}^2\]

이 성립하는 것도 쉽게 확인할 수 있습니다.

마찬가지로, $S=X_1+\cdots+X_n$일 때,

\[\begin{align*} E[S]&=E[X_1]+\cdots+E[X_n]\\ {\sigma_S}^2&={\sigma_{X_1}}^2+\cdots+{\sigma_{X_n}}^2+2\sum_{i\ne j}\text{cov}(X_i,X_j) \end{align*}\]

가 될 것입니다.

16 이산확률변수의 합과 컨볼루션

지난 강의에서 연속확률변수의 convolution에 대해 이야기되었습니다. 즉, 이산확률변수 $X$와 $Y$에 대하여 새로운 확률변수 $S=X+Y$의 확률밀도함수는

\[f_S=f_X\ast f_Y\]

의 관계를 만족시키며, 구체적으로는

\[(f_X\ast f_Y)(s)=\int_{-\infty}^\infty f(s-u)g(u)\,du\]

와 같이 나타난다고 했습니다.

이번 강의에서는 이산확률변수 $X$와 $Y$에 대한 convolution을 다룹니다. $X$가 이산확률변수라고 하는 것은, $X$가 취할 수 있는 값이 유한하거나, countable하다는 뜻이라고 했습니다. 그런데, convolution의 계산을 편하게 하기 위해서, $X$가 정수의 값만 가질 수 있다고 가정하고 있습니다. 마찬가지로 $Y$도 그 값이 정수인 경우만 이야기하고 있습니다.

이 경우에 convolution의 정의나 $S=X+Y$의 확률함수 식 계산은 연속확률분포에서보다 훨씬 간단합니다. 연속확률변수의 경우에서는 누적분포함수 $F_S(s)$를 먼저 구하기 위해서, 좌표평면 위에 $x+y\le s$라고 하는 부등식의 영역을 고려한 뒤 적분했어야 했습니다. 하지만, 이산확률변수의 경우, 확률질량함수 $P_X(s)$를 바로 구해도 됩니다. 그러면 부등식의 영역 대신

\[x+y=s,\qquad x,y\in\mathbb Z\]

와 같은 간단한 방정식을 생각하게 됩니다.

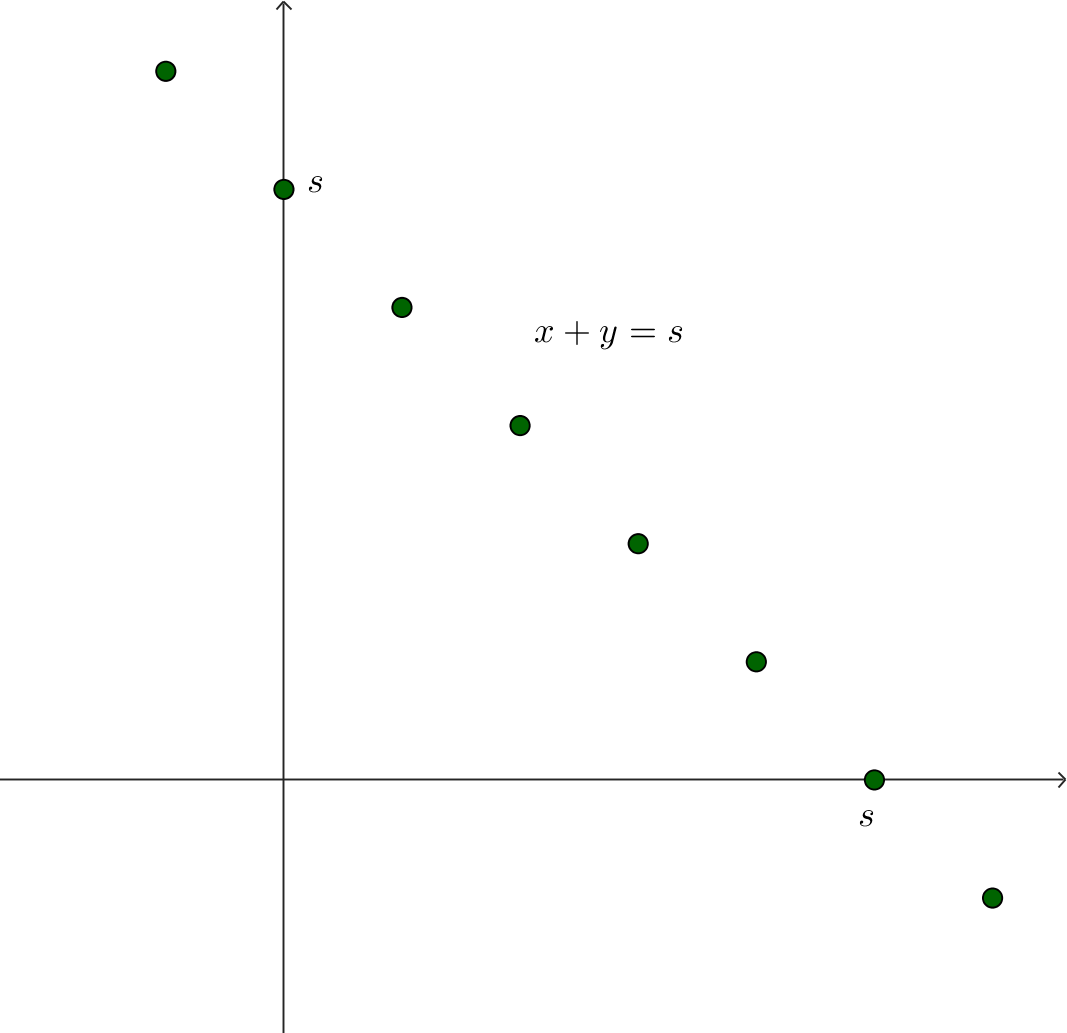
이때, $\mathbb Z$는 정수들의 집합으로, $x,y\in Z$는 $x$와 $y$가 모두 정수라는 사실을 표현한 것입니다. 이 디오판토스 방정식의 해는 무한히 많지만 countable한 정도로 많고, 그 해를 모두 쉽게 표현할 수 있습니다 ;

\[\begin{cases} x=k\\ y=s-k \end{cases}\quad(k\in\mathbb Z)\]

즉

\[\{(x,y)\in\mathbb Z^2:x+y=s\}=\bigcup_{k=-\infty}^\infty\{(k,s-k)\}\]

입니다. 따라서,

\[\begin{align*} P_S(s) &=P(S=s)\\ &=P(X+Y=s)\\ &=\sum_{k=-\infty}^\infty P(X=k, Y=s-k) \end{align*}\]

만약, $X$와 $Y$가 독립이면

\[P_S(s) =\sum_{k=-\infty}^\infty P_X(k)P_Y(s-k)\]

이것은 연속확률변수에서의 식과 거의 유사합니다. integral이었던 것이 summation으로 바뀌었고, PDF였던 것이 PMF로 바뀌었습니다.

정의 : convolution (discrete)
일반적으로, 두 함수 $f:\mathbb Z\to\mathbb R$, $g:\mathbb Z\to\mathbb R$에 대하여 새로운 함수 $f\ast g:\mathbb Z\to\mathbb R$을 $$(f\ast g)(s)=\sum_{k=-\infty}^\infty f(k)g(s-k)$$ 로 정의할 때, $f\ast g$는 $f$와 $g$의 convolution이라고 불립니다.

dicrete 버전의 convolution도 마찬가지로 결합법칙과 교환법칙이 성립합니다 ;

\[\begin{align*} ((f\ast g)\ast h)(s) &=\sum_{k\in\mathbb Z}(f\ast g)(k)h(s-k)\\ &=\sum_{k\in\mathbb Z}\sum_{m\in\mathbb Z}f(m)g(k-m)h(s-k)\\ &=\sum_{m\in\mathbb Z}f(m)\sum_{k\in\mathbb Z}g(k-m)h(s-k)\\ &=\sum_{m\in\mathbb Z}f(m)\sum_{j\in\mathbb Z}g(j)h(s-m-j)\\ &=\sum_{m\in\mathbb Z}f(m)(g\ast h)(s-m)\\ &=(f\ast(g\ast h))(s)\\[10pt] (f\ast g)(s) &=\sum_{k\in\mathbb Z}f(k)g(s-k)\\ &=\sum_{j\in\mathbb Z}f(s-j)g(j)\\ &=\sum_{j\in\mathbb Z}g(j)f(s-j)\\ &=(g\ast f)(s) \end{align*}\]

ex.

동전을 하나 던져서 앞면이 나오면 $X=1$, 뒷면이 나오면 $X=0$으로 대응시키는 확률변수 $X$를 생각하면, $X$의 PMF는

\[\begin{cases} P_X(0)&=\frac12\\ P_X(1)&=\frac12 \end{cases}\]

입니다. 또, 주사위를 하나 던져서 나온 숫자를 $Y$라고 하면, $Y$의 PMF는

\[\begin{cases} P_X(1)&=\frac16\\ P_X(2)&=\frac16\\ P_X(3)&=\frac16\\ P_X(4)&=\frac16\\ P_X(5)&=\frac16\\ P_X(6)&=\frac16 \end{cases}\]

입니다. 그러면, 당연히 $X$와 $Y$는 독립입니다. 새로운 확률변수 $S$를 $S=X+Y$로 정의하면 $S$의 값은 $1$, $2$, $\cdots$, $7$의 값을 가질 수 있고

\[\begin{cases} P_S(1)&=\frac1{12}\\ P_S(2)&=\frac16\\ P_S(3)&=\frac16\\ P_S(4)&=\frac16\\ P_S(5)&=\frac16\\ P_S(6)&=\frac16\\ P_S(7)&=\frac1{12} \end{cases}\]

와 같이 계산됩니다. 이것은

\[P_S(s)=(P_X\ast P_Y)(s)=\sum_{k=-\infty}^\infty P_X(k)P_Y(s-k)\]

로 계산될 수 있습니다.

ex. 6.8

강의에서는 이 동전-주사위 문제를 조금 더 확장해서, 나올 수 있는 근원사건의 수가 각각 $M$, $N$개이고 ($M\gt N$) 그 분포가 uniform한 두 확률변수 $X$, $Y$에 대해 더 말하고 있습니다. 이전 예와 비교했을 때 크게 다른 점은 없으므로 캡쳐로 대신하겠습니다.

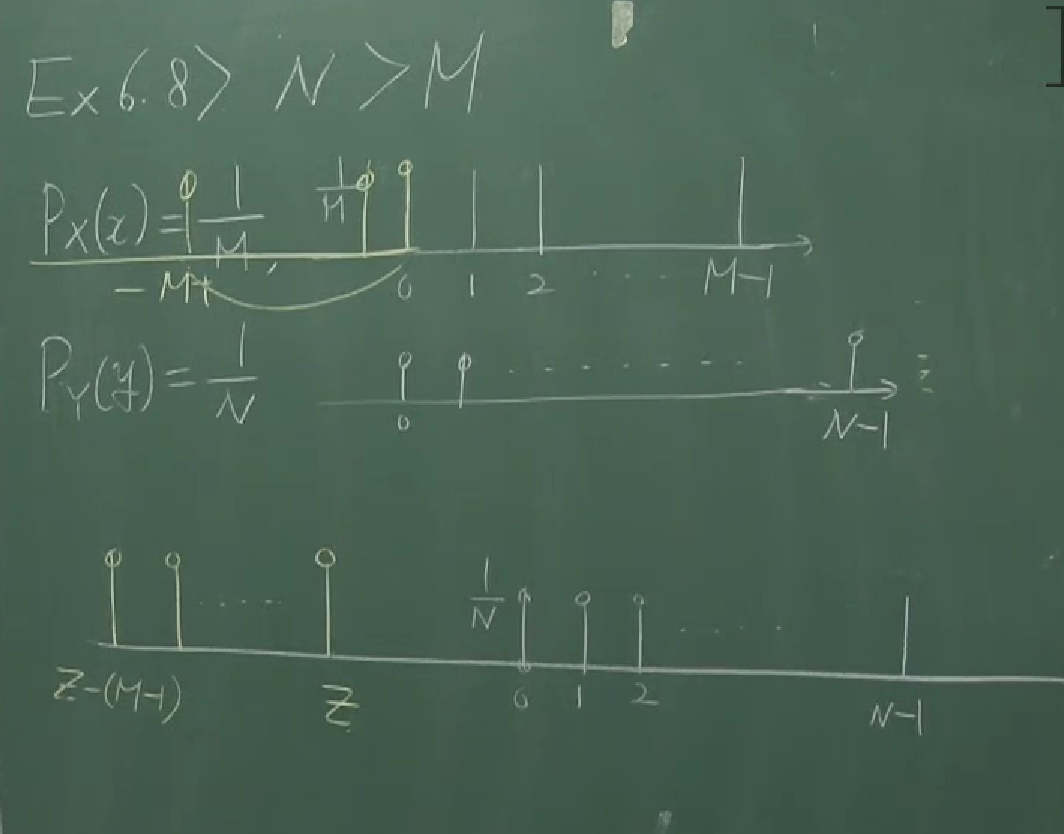
sums of independent binomial random variables

강의의 마지막에는 이항분포를 따르는 두 확률변수의 합에 대해 이야기합니다. 만약

\[X\sim B(n,p),\quad Y\sim B(m,p)\]

이면,

\[\begin{align*} P_X(x)&=\binom nxp^x(1-p)^{n-x}&&x=0,1,\cdots,n\\ P_Y(y)&=\binom myp^y(1-p)^{m-y}&&y=0,1,\cdots,m \end{align*}\]

입니다. 두 확률변수의 합인 $S=X+Y$의 확률질량함수를 구하기 위해서는 위의 두 PMF를 convolve하면 되는데 그때 사용되는 두 값은 $P_X(k)$와 $P_Y(s-k)$입니다. 만약 $k\lt0$이면 $P_X(k)=0$이고, $k\gt s$이면 $P_Y(s-k)=0$입니다. 따라서, convolution을 계산할 때 $0\le k\le s$인 항들만 계산하면 됩니다;

\[\begin{align*} P_S(s) &=(P_X\ast P_Y)(s)\\ &=\sum_{k=-\infty}^\infty P_X(k)P_Y(s-k)\\ &=\sum_{k=0}^sP_X(k)P_Y(s-k)\\ &=\sum_{k=0}^s\binom nkp^k(1-p)^{n-k}\times\binom m{s-k}p^{s-k}(1-p)^{m-s+k}\\ &=\sum_{k=0}^s\binom nk\binom m{s-k}p^s(1-p)^{m+n-s}\\ &=\left(\sum_{k=0}^s\binom nk\binom m{s-k}\right)p^s(1-p)^{m+n-s}\\ &\stackrel\ast=\binom{m+n}sp^s(1-p)^{m+n-s}\\ \end{align*}\]

입니다. 이때 $\star$는 Vandermonde’s identity라는 이름을 가지고 있다고 합니다. 강의에서는 이 식에 대한 증명을 조합론적으로 하고 있습니다. 만약 $m+n$개의 대상 중 $s$개를 뽑는다고 할 때, 특정한 $m$개의 대상을 A집단, 나머지를 B집단이라고 하면, 그 경우의 수는 A에서 $k$개를 뽑고 B에서 나머지 $s-k$개를 뽑는 경우를 다 더한 값과 같습니다. 따라서 Vandermonde’s inequality가 성립합니다.

이 등식에 대한 조금 더 수학적인 증명도 찾아보려 했는데, 위키피디아에서는 이항정리을 이용한 증명과 rectangular grid의 길찾기 문제를 이용한 증명이 나와있습니다. 하지만 근본적으로는 다 비슷한 증명이 아닐까 하는 생각이 듭니다. 이곳에는 수학적 귀납법을 사용한 증명도 있습니다.

sums of independent Poisson random variables

Poisson distribution에 대한 합도 생각해볼 수 있습니다. 만약

\[X\sim\text{Pois}(\lambda),\quad Y\sim\text{Pois}(\nu)\]

이면,

\[\begin{align*} P_X(x)&=\frac{\lambda^x}{x!}e^{-\lambda}\qquad(x=0,1,2,\cdots)\\ P_Y(y)&=\frac{\nu^y}{y!}e^{-\nu}\qquad(y=0,1,2,\cdots)\\ \end{align*}\]

입니다. 이번에도, $k\lt0$이거나 $k\gt s$이면 두 값 $P_X(k)$와 $P_Y(s-k)$ 중 하나의 값이 $0$이 되고, 따라서 $0\le k\le s$인 항들만 계산하면 됩니다;

\[\begin{align*} P_S(s) &=(P_X\ast P_Y)(s)\\ &=\sum_{k=-\infty}^\infty P_X(k)P_Y(s-k)\\ &=\sum_{k=0}^sP_X(k)P_Y(s-k)\\ &=\sum_{k=0}^s\frac{\lambda^k}{k!}e^{-\lambda}\times\frac{\nu^{s-k}}{(s-k)!}e^{-\nu}\\ &=\frac{e^{-(\lambda+\nu)}}{s!}\sum_{k=0}^s\frac{s!}{k!(s-k)!}\lambda^k\nu^{s-k}\\ &=\frac{e^{-(\lambda+\nu)}}{s!}(\lambda+\nu)^s\\ &=\frac{(\lambda+\nu)^s}{s!}e^{-(\lambda+\nu)} \end{align*}\]

따라서, $S$는 parameter가 $\lambda+\mu$인 Poisson distribution을 따릅니다 ;

\[X+Y\sim\text{Pois}(\lambda+\nu)\]

이것은, 어떻게 생각하면 당연한 결과입니다. 상점의 예를 들면, A 상점에는 시간당 $\lambda$명의 사람이 들어오고 B 상점에는 시간당 $\nu$명의 사람이 들어올 때, 어느 시점의 한 시간동안 A상점에 들어온 손님의 수를 $X$, B상점에 들어온 손님의 수를 $Y$라고 하면, $X$와 $Y$는 각각 위의 확률질량함수 $P_X$와 $P_Y$를 갖는다고 했었습니다. 만약, $S$를 $S=X+Y$라고 하면, (두 상점에 모두 들어간 손님이 없다고 할 때) $S$는 상점 A 혹은 상점 B에 들어간 손님의 수라고 볼 수 있고, 시간당 $\lambda+\nu$명의 손님이 들어온다고 예상되므로, $S\sim\text{Pois}(\lambda+\nu)$인 것입니다.

다시 말해, $X$는 어떤 사건 $A$가 단위시간당 $\lambda$번 일어난다고 가정할 때의 어느 단위시간동안 사건이 일어난 수이고, $Y$는 어떤 사건 $B$가 단위시간당 $\nu$번 일어난다고 가정할 때의 어느 단위시간동안 사건이 일어난 수일 때, 단위시간당 $\lambda+\nu$번의 사건 A 혹은 사건 B가 일어나므로, $X+Y$는 $\text{Pois}(\lambda+\nu)$를 따릅니다.

17 두 변수의 변환 함수

일변수 실함수의 변환함수

이번 강의에서는 $g$가 다변수벡터함수인 경우, 다시 말해 $g:\mathbb R^n\to\mathbb R^n$인 경우를 다룹니다. 그 중에서도 가장 간단한 경우인 $g:\mathbb R^2\to\mathbb R^2$인 경우를 고려합니다.

시작하기에 앞서서, $g$가 일변수 실함수인 경우를 복습해보겠습니다. $\langle14\rangle$에서 이미 비슷한 계산을 해본 적이 있습니다. 함수 $g:\mathbb R\to\mathbb R$이 일대일함수이고 미분가능하며, 두 확률변수 $X$, $Y$가 $Y=g(X)$를 만족시킨다고 가정하겠습니다. 그러면 $g$는 단조함수일 수밖에 없습니다. 왜냐하면, 집합 $M=\{(x,y)\in\mathbb R^2:x\lt y\}$는 connected set이고, $h(x,y)=g(x)-g(y)$로 정의된 $h:M\to\mathbb R$는 연속함수이기 때문에, $h$의 image인 $h(M)$은 connected입니다. $g$가 일대일함수라는 사실로부터 $0\notin h(M)$이고, 따라서 $h(M)$은 $(-\infty,0)$ 안에 들어있거나 아니면 $(0,\infty)$ 안에 들어있습니다. 전자의 경우에는 $g$가 monotonically increasing하고, 후자의 경우에는 monotonically decreasing합니다.

monotonically increasing한 경우에는

\[\begin{align*} f_Y(y) &=\frac d{dy}F_Y(y)\\[10pt] &=\frac d{dy}P(Y\le y)\\[10pt] &=\frac d{dy}P(g(X)\le y)\\[10pt] &=\frac d{dy}P(X\le g^{-1}(y))\\[10pt] &=\frac d{dy}F_X(g^{-1}(y))\\[10pt] &=\frac{dx}{dy}\cdot\frac d{dx}F_X(g^{-1}(y))\\[10pt] &=\frac{\frac d{dx}F_X(g^{-1}(y))}{\frac{dy}{dx}}\\[10pt] &=\frac{f_X(g^{-1}(y))}{g'(g^{-1}(y))} \end{align*}\]

입니다. monotonically decreasing한 경우에는 그 결과가

\[f_Y(y)=-\frac{f_X(g^{-1}(y))}{g'(g^{-1}(y))}\]

로 나오므로, 이것을 하나의 식으로

\[f_Y(y)=\frac{f_X(g^{-1}(y))}{|g'(g^{-1}(y))|}\]

와 같이 쓸 수 있었습니다. $x=g^{-1}(y)$로 표현하면

\[f_Y(y)=\frac{f_X(x)}{|g'(x)|}\]

입니다.

이변수 벡터함수의 변환함수

$g:\mathbb R^2\to\mathbb R^2$인 경우도 비슷합니다. 다만, 위의 식의 분모에 $g’(x)$이었던 것이 jacobian으로 바뀝니다. 네 확률변수 $X$, $Y$, $Z$, $W$에 대하여

\[(Z,W)=g(X,Y)\]

의 관계가 있다고 하겠습니다. 만약, $(x,y)$의 한 근방과 $(z,w)=g(x,y)$의 한 근방에서 $g$가 일대일대응이면

\[f_{ZW}(z,w)=f_{XY}(x,y)\times\left|\frac{\partial(x,y)}{\partial(z,w)}\right|\]

이 성립합니다. 왜냐하면, $g|S:S\to T$가 일대일대응인 모든 $S,T\subset\mathbb R^2$에 대하여

\[\begin{align*} \iint_Tf_{ZW}(z,w)\,dz\,dw &=P\left((z,w)\in T\right)\\ &=P\left((x,y)\in S\right)\\ &=\iint_Sf_{XY}(x,y)\,dx\,dy\\ &\stackrel\star=\iint_T f_{XY}\left(h_1(z,w),h_2(z,w)\right)\cdot\left|\frac{\partial(x,y)}{\partial(z,w)}\right|\,dz\,dw \end{align*}\]

이기 때문입니다. 이때, $h$는 $g$의 역함수로서

\[(x,y)=h(z,w)=\left(h_1(z,w),h_2(z,w)\right)\]

이고, $\star$는 다변수 미적분(multivariate calculus)에서 얻을 수 있는 결과로서, $\lvert\frac{\partial(x,y)}{\partial(z,w)}\rvert$는 jacobian matrix의 determinant에 절댓값을 취한 것입니다;

\[\left|\frac{\partial(z,w)}{\partial(x,y)}\right| =\left|\text{det}\left(\begin{bmatrix} \frac{\partial x}{\partial z}&\frac{\partial x}{\partial w}\\[5pt] \frac{\partial y}{\partial z}&\frac{\partial y}{\partial w} \end{bmatrix}\right)\right| =\begin{vmatrix} \frac{\partial x}{\partial z}&\frac{\partial x}{\partial w}\\[5pt] \frac{\partial y}{\partial z}&\frac{\partial y}{\partial w} \end{vmatrix} =\left|\frac{\partial x}{\partial z}\times\frac{\partial y}{\partial w}-\frac{\partial x}{\partial w}\times\frac{\partial y}{\partial z}\right|\]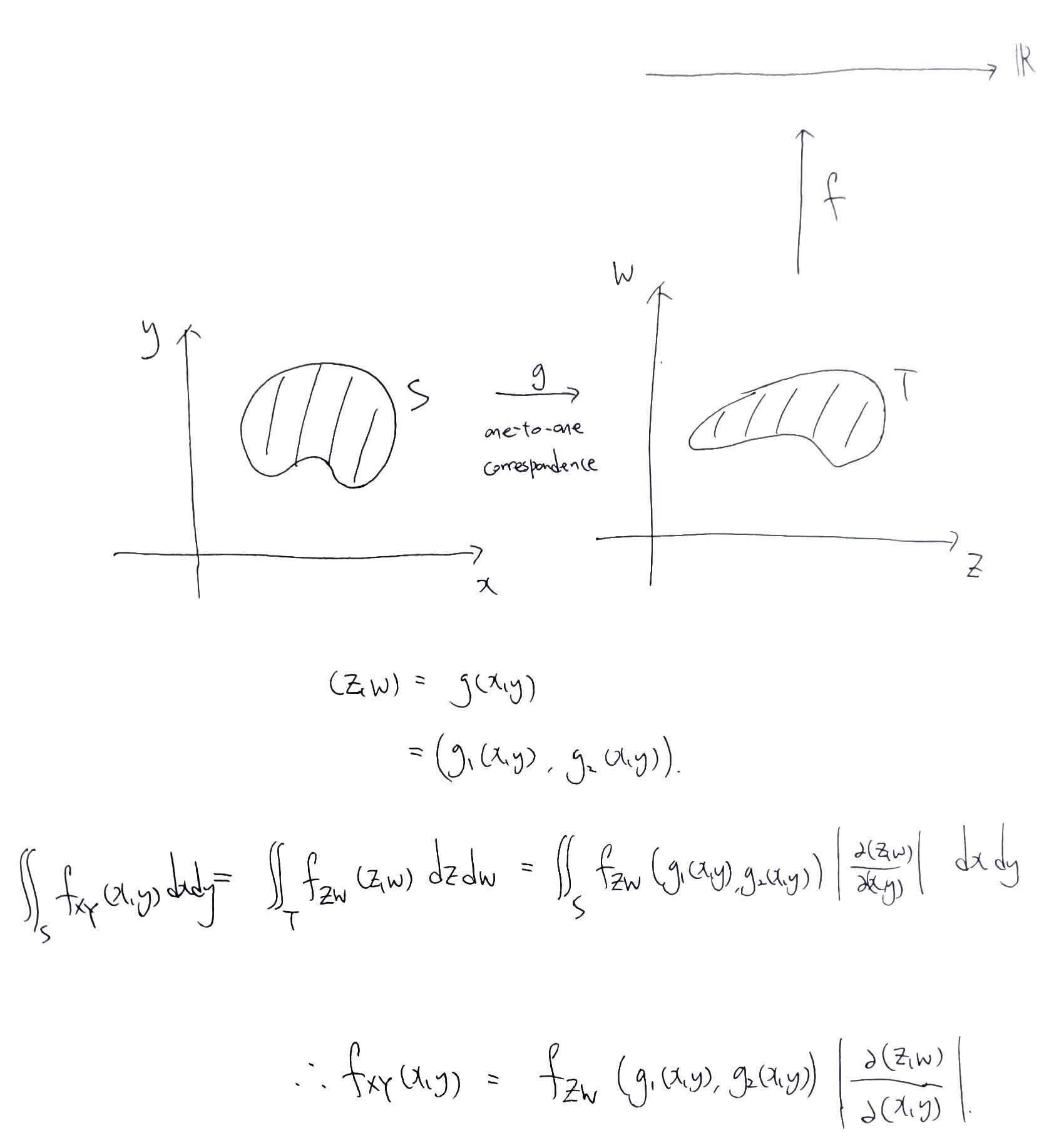

ex 6.16

예를 들어,

\[\begin{align*} U&=X+Y\\ V&=X-Y \end{align*}\]

이고, $f_{XY}(x,y)$가

\[f_{XY}(x,y)=\frac1{2\pi}e^{-\frac{x^2+y^2}2}\]

로 주어져있을 때, $f_{UV}(u,v)$를 구하는 문제를 생각해보겠습니다. 확률변수 $U$, $V$, $X$, $Y$ 대신 확률변수의 값 $u$, $v$, $x$, $y$로 바꿔서 정리하면

\[\begin{align*} u&=x+y\\ v&=x-y \end{align*}\]

이고, $(U,V)$와 $(X,Y)$의 관계를 서로 바꾸면

\[\begin{align*} x&=\frac12u+\frac12v\\ y&=\frac12u-\frac12v \end{align*}\]

입니다. 따라서

\[\begin{align*} f_{UV}(u,v) &=f_{XY}(x,y)\times\left|\frac{\partial(x,y)}{\partial(u,v)}\right|\\ &=f_{XY}\left(\frac12u+\frac12v,\frac12u-\frac12v\right)\times \begin{vmatrix}\frac12&\frac12\\\frac12&-\frac12\end{vmatrix}\\ &=\frac12f_{XY}\left(\frac12u+\frac12v,\frac12u-\frac12v\right)\\ \end{align*}\]

입니다.

추가예시

또다른 예시로, DeGroot, Probability and Statistics, 4ed의 Example 3.9.9를 들어보겠습니다. 앞서의 예시와 거의 비슷한데, 덧셈과 뺄셈이었던 것이 곱셈과 나눗셈으로 바뀌었습니다.

\[f_{UV}(u,v)= \begin{cases} 4uv &0<u,v<1\\ 0. &\text{(otherwise)} \end{cases}\]

이고, $X=\frac UV$, $Y=UV$일 때, $f_{XY}(x,y)$를 계산해보는 문제입니다.

문제를 풀기에 앞서 $f_{XY}$가 정말 PDF의 역할을 하는지 확인해봅니다 ;

\[\begin{align*} P\left((u,v)\in S\right) &=\iint_Sf_{UV}(u,v)\,du\,dv\\ &=\int_0^1\int_0^14uv\,du\,dv\\ &=1. \end{align*}\]

함수 $r=(r_1,r_2):\mathbb R^2\to\mathbb R^2$를

\[\begin{aligned} x&=r_1(u,v)=\frac uv\\ y&=r_2(u,v)=uv \end{aligned}\]

로 정의하면 이 함수 $r$은

\[S=\{(u,v)\in\mathbb R^2:0\lt u,v\lt 1\}\]

에서 미분가능합니다. $r$은 일대일함수이기도 한데 만약 $\left(\frac{u_1}{v_1},u_1v_1\right)=\left(\frac{u_2}{v_2},u_2v_2\right)$ 이면

\[\begin{align*} {u_1}^2&=\left(\frac{u_1}{v_1}\right)\times(u_1v_1)=\left(\frac{u_2}{v_2}\right)\times(u_2v_2)={u_2}^2\\ {v_1}^2&=\left(\frac{u_1}{v_1}\right)\div(u_1v_1)=\left(\frac{u_2}{v_2}\right)\div(u_2v_2)={v_2}^2 \end{align*}\]

이어서 $(u_1,v_1)=(u_2,v_2)$ if $r(u_1,v_1)=r(u_2,v_2)$이기 때문입니다.

집합 $T$를 $T=r(S)$라고 하면, $r$은 $S$와 $T$ 사이에서 일대일대응입니다. $r$의 역함수를 $s$라고 하면,

\[\begin{align*} u&=s_1(x,y)=\sqrt{xy}\\ v&=s_2(x,y)=\sqrt{\frac yx}. \end{align*}\]

입니다. $T$를 구해보면

\[\begin{align*} (x,y)\in T &\iff\left(s_1(x,y),x_2(x,y)\right)\in S\\ &\iff(u,v)\in S\\ &\iff 0<u<1\quad\&\quad0<v<1\\ &\iff 0<\sqrt{xy}<1\quad\&\quad0<\sqrt{\frac yx}<1\\ &\iff x>0\quad\&\quad y>0\quad\&\quad y<\frac1x\quad\&\quad y<x\\ &\iff 0<y<\min\left(x,\frac1x\right),\\ T&=\left\{(x,y)\in\mathbb R^2:0<y<\min\left(x,\frac1x\right)\right\} \end{align*}\]

입니다;

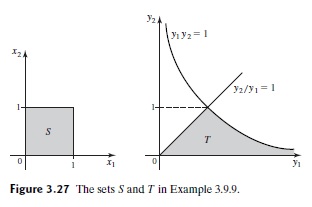
한편,

\[\begin{align*} \frac{\partial(u,v)}{\partial(x,y)} &=\det \begin{bmatrix} \frac{\partial u}{\partial x}&\frac{\partial u}{\partial y}\\[10pt] \frac{\partial v}{\partial x}&\frac{\partial v}{\partial y} \end{bmatrix}\\ &= \begin{vmatrix} \frac12\sqrt{\frac yx} &\frac12\sqrt{\frac xy}\\[10pt] -\frac12\sqrt{\frac y{x^3}} &\frac12\sqrt{\frac1{xy}} \end{vmatrix}\\ &=\frac1{2x}. \end{align*}\]

이고, 따라서

\[\begin{align*} f_{XY}(x,y) &=f_{UV}\sqrt{xy} &&\sqrt{\frac yx}\qquad(x,y)\in T\\ &=\frac{2y}x &&0<y<\min\left(x,\frac1x\right) \end{align*}\]

입니다.

이변수 실수함수의 변환함수

이번에는 $g:\mathbb R^2\to\mathbb R$인 경우입니다. 이경우에는 jacobian matrix가 정사각행렬이 아니므로 기존의 방법을 그대로 적용할 수는 없습니다. 확률변수 $X$, $Y$의 PDF가 주어져있고, 함수 $g$를 통해서 새로운 확률변수 $Z=g(X,Y)$를 정의할 때, jacobian 행렬은 $1\times2$ 행렬인 것처럼 보이기 때문입니다. 이때에는, $W$라는 보조적인(auxiliary) 확률변수를 도입하여 jacobian matrixf를 정사각행렬로 만들어주는 트릭이 존재합니다;

\[\begin{align*} Z&=g(X,Y)\\ W&=X \end{align*}\]

로 두는 것입니다.

ex 6.20

만약 $U=XY$이면,

\[\begin{align*} U&=XY\\ W&=X \end{align*}\]

이라고 쓸 수 있고,

\[\begin{align*} u&=xy\\ w&=x \end{align*}\]

로부터

\[\begin{align*} \frac{\partial(u,w)}{\partial(x,y)}&=\begin{vmatrix}y&x\\1&0\end{vmatrix}=|-x|=|x|\\ \frac{\partial(x,y)}{\partial(u,w)}&=\frac1{\frac{\partial(u,w)}{\partial(x,y)}}=\frac1{|w|} \end{align*}\]

입니다. 따라서,

\[f_{UW}(u,w)=f_{XY}(x,y)\times\frac1{|w|}=\frac{f_{XY}\left(w,\frac uw\right)}{|w|}\]

입니다. 만약 $X$, $Y$가 joint (standard) normal 이어서

\[f_{XY}(x,y)=\frac1{2\pi}e^{-\frac{x^2+y^2}2}\]

이라면,

\[\begin{align*} f_{UW}(u,w) &=\frac{f_{XY}\left(w,\frac uw\right)}{|w|}\\ &=\frac1{2\pi|w|}e^{-\frac{w^2+\frac{u^2}{w^2}}2} \end{align*}\]

이 될 것입니다.

generating Gaussian distribution from the uniform distribution

이제, $\langle14\rangle$에서 언급되었던, uniform distribution을 따르는 확률변수를 통해서 normal distribution을 만드는 방법을 소개할 수 있습니다. 조금 더 정확하게는 unifrom distribution을 따르는 두 확률변수로부터 standard joint normal한 두 확률변수를 얻어낼 수 있습니다.

두 확률변수 $X$, $Y$가 $0$과 $1$ 사이의 uniform distribution을 따른다고 하겠습니다 ;

\[\begin{align*} X&\sim U(0,1)\\ Y&\sim U(0,1) \end{align*}\]

더 나아가, $X$와 $Y$가 독립이라고 하겠습니다. $X$와 $Y$의 PDF는 각각

\[\begin{align*} f_X(x)&=1&&(0\lt x\lt 1)\\ f_Y(y)&=1&&(0\lt y\lt 1) \end{align*}\]

로 주어지고, $f_{XY}(x,y)=1$입니다. 새로운 확률변수 $U$와 $V$를

\[\begin{align*} U&=\sqrt{-2\log X}\cos 2\pi Y\\ V&=\sqrt{-2\log X}\sin 2\pi Y \end{align*}\]

로 두면 ($\log$는 자연로그입니다.)

\[\begin{align*} u&=\sqrt{-2\log x}\cos 2\pi y\\ v&=\sqrt{-2\log x}\sin 2\pi y \end{align*} \tag{$\ast$}\]

로부터

\[\begin{align*} \frac{\partial(u,v)}{\partial(x,y)} &=\begin{vmatrix} -\frac{-\cos 2\pi y}{x\sqrt{-2\log x}} &-2\pi\sqrt{-2\log x}\sin2\pi y\\ -\frac{-\sin 2\pi y}{x\sqrt{-2\log x}} & 2\pi\sqrt{-2\log x}\cos2\pi y \end{vmatrix} =-\frac{2\pi}x\\ \frac{\partial(x,y)}{\partial(u,v)} &=\frac1{\frac{\partial(x,y)}{\partial(u,v)}}=-\frac x{2\pi} \end{align*}\]

이고, 따라서

\[\begin{align*} f_{UV}(u,v) &=f_{XY}(x,y)\times\lvert\frac{\partial(x,y)}{\partial(u,v)}\rvert\\ &=\frac x{2\pi}\\ &=\frac1{2\pi}e^{-\frac12(u^2+v^2)} \end{align*}\]

입니다. 따라서, $U$, $V$는 standard joint normal입니다.

$(x,y)$를 $(u,v)$로 변환하는 식 $(\ast)$은 관찰해볼 여지가 있는 재미있는 식인 것 같습니다. $(u,v)$를 복소수로 생각하면, $\sqrt{-2\log x}$는 이 복소수의 크기(amplitude)를 나타내고, $2\pi y$는 이 복소수의 편각(argument)를 나타냅니다;

$(u,v)=\sqrt{-2\log x}e^{2\pi yi}$

$x$가 $(0,1)$ 안에서 움직이므로, $\sqrt{-2\log x}$는 $(0,\infty)$ 안에서 움직입니다. 또, $y$도 $(0,1)$ 안의 실수이므로, $0\lt2\pi y\lt1$입니다. 그러니까, $(x,y)$가 unit square $(0,1)^2$ 내부에서 움직이는 동안, $(u,v)$는 복소평면의 한 branch cut

\[\{(u,v):u\ge0, v=0\}\]

을 제외한 모든 곳을 움직입니다. 하지만 이 부분을 무시하면, $(u,v)$는 이차원 평면 전체를 움직인다고 생각할 수 있습니다.

generating exponential from the uniform distribution

$X\sim U(0,1)$인 확률변수 $X$에 대하여, 새로운 확률변수 $Y=g(X)$를 함수 $g$로 정의할 때, $Y$가 $\lambda=1$인 exponential PDF를 가지기 위해서는 어떤 함수 $g$를 적용해야 할 지 고민해봅니다. 문제를 단순하게 만들기 위해 $g$가 단조감수함수라고 가정하겠습니다. 따라서 $g$는 일대일대응이고, 역함수를 가지고 있습니다.

$X$의 PDF는

\[f_X(x)=1\qquad(0\lt x\lt 1)\]

이고, CDF는

\[F_X(x)=x\qquad(0\lt x\lt 1)\]

입니다. 한편, $Y$는

\[\begin{align*} f_Y(y)&=e^{-y}\\ F_Y(y)&=1-e^{-y} \end{align*}\]

를 만족시킵니다. 그러면

\[\begin{align*} 1-e^{-y} &=P(Y\le y)\\ &=P(X\ge g^{-1}(y))\\ &=1-F_X\left(g^{-1}(y)\right)\\ &=1-g^{-1}(y) \end{align*}\]

따라서,

\[g^{-1}(y)=e^{-y}\]

이고,

\[g(x)=-\log x\]

로 두면 된다는 것을 확인할 수 있습니다.

회고

「확률 및 통계」 강의 강의에 대한 정리는 일단 여기까지 하도록 하겠습니다. 늘 그렇지만 공부하고 싶은 것이 참 많다고 새삼 느낍니다. 한편으로 생각하면, 학부나 대학원때 더 공부를 열심히 할 걸 하는 생각도 들지만, 그땐 그때 나름대로 열심히 했으니 어쩔 수 없을 것 같습니다.

가장 궁금하면서, 제대로 공부하고 싶은 주제는 dirac delta function입니다. delta function의 제대로 된 정의를 measure-theoretic하게 공부해보고 싶습니다. 확률론을 전공한 몇몇 지인들은 이것들을 오래전부터 이것을 잘 알고 있었을 거라 생각하니, 샘이 나기도 합니다. 특히나, covolution 연산이 어떤 의미에서 abelian group을 형성하는데, 그 group의 identity가 delta function이 된다는 아주 재미있는 사실은 정말 공부하고 싶습니다. 더 나아가서 delta function은 양자역학과도 연관이 있다고 합니다. 물리에서 delta function이 중요하다고도 합니다, 그리고 물리에서 말하는 delta function과 수학에서 말하는 delta function은 (그래서, 얼마 전 물리를 전공한 친구와 강화도 여행을 갔을 때 이에 대해 물어봤었는데, 그 친구는 이에 대해 아주 잘 알지는 못했던 것 같습니다.) delta function에 대한 책도 하나 찾아두기는 했습니다. 시간이 될 지 정말 모르겠지만, 만약 시간이 허락한다면, 한번 긴히 공부해보고 싶습니다.

또 하나의 주제는 differential/difference equation입니다. 각각 exponential/geometric distribution과 연관이 있다고 강의에서 언급되었는데, 구체적으로 어떻게 연관되어 있는지 참 궁금합니다. 사실, difference equation 자체는 더 볼 것이 없을지도 모르겠습니다. 이전 포스팅이었던 행렬의 대각화의 직접적인 활용이기 때문에 더 많이 쓸 것은 없어보입니다. 그런데 differential equation에 관해서는, 해당 내용을 적으면서 ‘내가 미분방정식에 대해 모르는 내용이 많구나’하고 느끼게 되었습니다. 간단한 일변수 homogenous linear differential equation $y’=ay$ 같은건 당연히 그 원리를 명확하게 알고 있습니다. 이것이 (system of) 이변수 homogenous linear differential equation이 되는 순간 사인함수나 코사인함수, 혹은 지수함수의 쌍이 generalized soultions를 이루게 되는데 그 원리에 대해 아주 자세히 알고있지 못합니다. 정확히 알려면 matrix exponentiation에 대해 알아야하고, 그것이 강의에서 언급되기도 했었습니다. 더 나아가, 이 경우의 jacobian matrix가 어떻게 differential equation에 활용되는지 하는 것도 알아야 할 것입니다.

또다른 주제는 Fourier transform, Fourier series, Wavelet transform입니다. 이에 관해서는 행렬의 대각화 글을 마칠 때에도 언급했던 적이 있습니다. 이 포스트는 Fourier transform 직전에 마쳤습니다. Fourier transform은 수학적으로도 매우 중요할 뿐만 아니라, 신호처리나 음성인식 같은 활용 측면에서 너무나도 중요하다고 알려져있습니다. 어떤 구간에서 정의된 임의의 연속함수가 사인함수와 코사인함수들의 급수를 이룬다는 Fourier series의 사실은 참 매력적입니다. 이것이, (어떤 종류의) 사인함수와 코사인함수들의 집합이 Hilbert space의 complete orthogonal system을 이룬다는 선형대수적인 사실과 연관되어 있다는 것도 너무 재밌습니다. 그리고 Fourier series처럼 discrete한 레벨의 논의에서 더 나아가면 continuous한 레벨의 Fourier transform이 됩니다. 여기에서 (강의에서 언급된) convolution은 중요한 연산의 역할을 하게 됩니다. 이 주제를 공부하고 싶은 또다른 이유는, 얼마 전에 포트폴리오를 작성하면서 2년 반쯤 전에 했던 연구가 생각나서였습니다. Fourier series/transform과 상당히 닮은, Wavelet이라는 개념은 상당히 매력적으로 보입니다. 그때에는 시간이 없어서 원리를 깊이 이해하지 못한 채로 코드를 짰어야 했었고, 아직까지도 이해해야 할 부분들이 많이 남아있습니다. 그때의 연구가 완전히 성공적이었던 것도 아니었지만, 어쨌든 그 연구를 다른 사람에게 설명하려 할 때면, 약간의 마음의 가책과 확실하게 알아야 겠다는 마음을 가지게 됩니다.

또한, 확률과정(stochastic process)에 대해서도 긴히 알아야 할 필요가 있습니다. 강의에서도 몇번이고 강조하셨지만, stochastic process는 그 쓰임새가 무궁무진합니다. 강화학습의 세팅에서도 확률과정은 기본이고, 심지어는 ARIMA와 같은 고전적인 시계열 솔루션은 시계열 데이터를 stochastic process로 간주합니다. 그래도, 이번 확률 및 통계 강의를 들으면서 그 기본단계를 정확하게 이해했다고 생각하니, 나중에 혹시 ARIMA를 다시 배우게 되더라도 이번에 배웠던 것이 도움이 많이 될 것 같습니다.

통계의 일반적인 사항에 대해서도 공부해야 합니다. 이 강의를 정리하는 시발점이 되었던 통계스터디 모임의 원래 목적은 통계를 공부하는 것이었습니다. 그런데 이 강의 자체도 통계에 대해서는 아주 많이 다루고 있지 않고, 정작 이 포스트에서도 그 부분은 제외하고 일단 적어놓은 상태입니다. 때문에, 다시 기회가 된다면, 통계 일반에 대해서 공부해야 할 필요가 있습니다.

---

수학을 좋아하는 사람이라, 기술블로그를 열겠다 해놓고 정작 수학 이야기만 잔뜩 적어보았습니다. 한 번은 선형대수에 빠져서, 또 한 번은 확률론에 빠져서 열심히 적었습니다. 주변 사람들로부터, ‘코딩/데이터사이언스’를 공부하는 것만도 바쁘고 그게 더 우선인데, 왜 수학에만 매진하고 있냐’는 말을 들을 정도였습니다. 하지만, 재미있었고 또 유익했기 때문에, 후회하지는 않습니다.

앞으로는 코딩적인 이야기를 많이 포스팅으로 남겨보려고 합니다. 최근 구직활동을 하며 “실무에서는, 프로그래밍적인 능력을 우선으로 치는구나”라는 것을 느꼈습니다. 아무리 수학에 대한 지식이 어떻건 간에, 중요한 것은 코딩능력이라고 느낍니다.

최근 냈었던 이력서/포트폴리오에 다음과 같은 기술 스택 그래프를 다음과 같이 적어봤었습니다.

조금 솔직하게 적다보니 저렇게 적게 되었습니다. 그리고, pytorch에 대한 능력이 저렇게 낮다는 것이, 조금 더 정확하게는, pytorch에 대한 낮은 능력을 이력서나 포트폴리오에 적는 것이 별로 좋지 않다고 느꼈습니다. 물론, pytorch를 잘하지도 못하면서 저 그래프는 높게 그릴 수도 있겠지만은, 거짓말은 하고 싶지 않기 때문에, 실무적인 코딩능력을 보완하는 것을 당장의 목표로 잡아보려 합니다. 우선 keras/tensorflow부터 시작하여 차근차근 필요한 내용들을 점검하고, 최종적으로는 pytorch로 갈 예정입니다. 구체적으로는, 머신러닝의 기본적인 알고리즘들인 MLP, CNN, RNN (혹은 그 외) 정도를 각각 keras / tensorflow / pytorch로 구현해보는 것을 그 목표로 합니다. 여러 개의 정도의 지도학습 문제 (regression, classification, 등)에 대하여 그것들을 각각 다른 framework로 구현해보면 좋은 포트폴리오 자료는 물론 두고두고 열어볼 수 있는 참고자료가 될 것입니다.

이것은, 약 1년 전에 교수님께서 저에게 요청하셨던 사항이기도 한데, 그때 교수님의 말씀을 듣지 않고 속을 썩였던 것에 대한 반성일지도 모르겠습니다. 그래도 그 당시에, numpy에 대해서만큼은 폭넓게, 그리고 나름대로는 깊게 공부하여 발표까지 했던 기억이 있습니다. 꼭 그런 정도로까진 아니더라도, 비슷한 정도로 keras, tensorflow, pytorch에 대해 공부하고, 결국은 위의 기술 스택 그래프를 (양심에 찔리지 않고) 늘리는 것이 당장의 목표입니다.

참고한 자료들

1. KOCW(Korea Open Course Ware), 『확률과 통계』, 한양대학교 이상화 교수님 강의
2. DeGroot, Probability and Statistics, 4ed
3. The Book of Statistical Proofs
4. Introduction to Probability, Statistics and Random Process
5. Mathematics Stack Exchange
6. G. Strang, Linear Algebra and Its Applications, 4ed
7. StatQuest - Covariance, Clearly Explained!!!