자동차의 두 바퀴는 같은 거리를 이동하는가

3월 16일 일요일 새벽 6시 46분. 일기에 이렇게 썼다.

꿈에서 어떤 수학문제를 생각했고 그 문제를 풀었다고 생각해서 뿌듯했는데 일어나고 보니 무슨 문제를 풀었는지 까먹었다. 하지만 깨어나서 눈을 감고 일어나기 전에 자동차의 두 앞바퀴에 대한 문제를 생각하고 이걸 math exchange에 질문하고 싶어졌다. 이 문제는 대학 2학년 때 K 교수님의 교양 수업에서 내가 생각했던 문제와도 조금 비슷하고 아마 differential geometry의 기본적인 문제가 될 것 같다.

전날인 토요일에는 매우 피곤했다. 이번 환절기는 그냥 지나가나 싶었지만 어김없이 감기 기운이 스멀스멀 올라왔고 그때문에 토요일에 본가에 내려가려던 계획을 다음날로 미뤘던 것이다. 일기에 저 글을 쓴 후 바로 math exchange에 글을 썼다. 머릿속에 있는 그림, 그러니까 해당 문제에 대한 trivial case의 그림을 geogebra로 그려서 첨부하기도 했다.

글을 게시한 후 몇 시간동안은 두 개 정도의 댓글만 달렸다. 그 댓글들에 나는 적절하게 답글을 적을 수 있었다. 그만큼 내가 제기한 문제는 명확했고 구체적이었다. 첫번째 댓글은 자동차의 두 바퀴가 앞의 두 바퀴가 아닌 뒤의 두 바퀴여야 한다는 것이어서 나는 해당사항을 글에 반영했다. 두번째 댓글은 왜 꼭 trajectile이 원호와 선분으로 이루어져야 한다고 생각했냐는 질문이었고 나는 trivial case를 생각한 것뿐이라고 대답했다. 모든 걸 elementary level에서 계산할 수 있는 예시를 든 것이고 이 예시에서 내 문제의 답은 yes인데, 일반적인 경우에 대해서는 어떻게 묘사되고 서술되고 계산될 수 있는지 묻는 것이라고도 부연했다.

그리고는 글을 볼 새가 없었다. 나는 본가에 내려가 가족행사에 참여해야 했다. 11시에 청량리에서 출발하는 itx 열차를 타고 내려갔다가 저녁 6시쯤 되어서야 서울 집으로 귀가할 수 있었다. 매우 피곤하여 푹 쉬다가 아까 수학 질문글을 올렸음을 기억해내고 밤 10시쯤에야 해당 글을 다시 확인했다. 두번째 댓글을 쓴 Ted Shifrin이라는 사람이 이 문제에 대한 풀이를 써주었다. 아주 간결하고 깔끔하게 적힌 글이었다. 새벽 1시반까지 해당 풀이를 이해하려고 관련 내용을 간단히 공부하고 질문자와 댓글을 주고받았고 마침내 주요한 내용들은 다 이해할 수 있게 되었다.

정말로 math exchange는 대단한 사람들이 많은 공간이다. 수학을 쬐끔 안다고 하여도 결코 여기서 잘난 체를 할 수 없다. 풀이를 써준 Ted Shifrin이라는 사람이 어떤 사람인가 하고 보니 reputation이 12만 정도 되는 사람이고 미국의 조지아 공립대학에서 36년간 differential geometry와 algebraic geometry을 연구한, 지금은 퇴직한 교수님이었다. 풀이의 Ted Shifrin이 펼친 논리에서 조금 어려운 부분이 있었는데 그 부분에 대해서는 자기가 쓴 책의 1.3 섹션을 참고하라고 했다. 그러니까 여기는 석사나 박사 정도가 방귀뀌는 곳이기도 하지만 가끔 교수님들이 등장해 완벽한 설명을 해내곤 한다.

기분이 좋았던 건 내가 제기한 이 문제가 좋은 문제라는 평가를 들었다는 것이다. 두 사람에게서 “A (very) nice question”이라는 말을 들었다. 물론 그들도 재밌는 문제라고 생각했겠지만 그 누구보다도 내가 제일 흥미롭게 느꼈다. 3월 26일 기준으로 해당 글은 49개의 upvote를 얻었고 Ted Shifrin의 풀이도 38개의 upvote를 얻었다. 지금까지 math exchange에 질문글을 올리거나 아니면 풀이를 작성했을 때에도 내가 받은 upvote 수가 2개를 넘지 않았던 것을 생각하면 이례적이다. 내 reputation도 270에서 792 정도로 세 배 가까이 뛰었다.

풀이글은 하나밖에 없긴 하지만 꽤 많은 사람들이 댓글을 달아주었고 나는 그것들을 다 보진 않았다. 또한 Ted Shifrin의 풀이도 주요한 부분은 이해했지만 완전히 다 이해하진 못했다. 이해하려면 그의 책 Differential Geometry를 조금 읽어야 할텐데 다른 공부하고 있는 것이 있어서 그것을 공부할 시간은 없는 것이다.

이 포스트에서는 내가 제기한 문제를 다시 적어보고 이 문제에 대한 Ted Shifrin의 풀이를 좀 더 자세하게 풀어서 써본다. 모든 것은 stack exchange의 원래 글에 충분히 자세히 적혀있다. 하지만 영어로 된 것을 한글로 바꿔놓으면 더 보기가 좋을 것이다. 또한 Ted Shifrin의 풀이를 내가 나중에 직접 다시 읽으면 이해를 못할 것 같아서 어제 이해한 것을 부연하여 자세히 써내려가보려 한다.

1. 문제

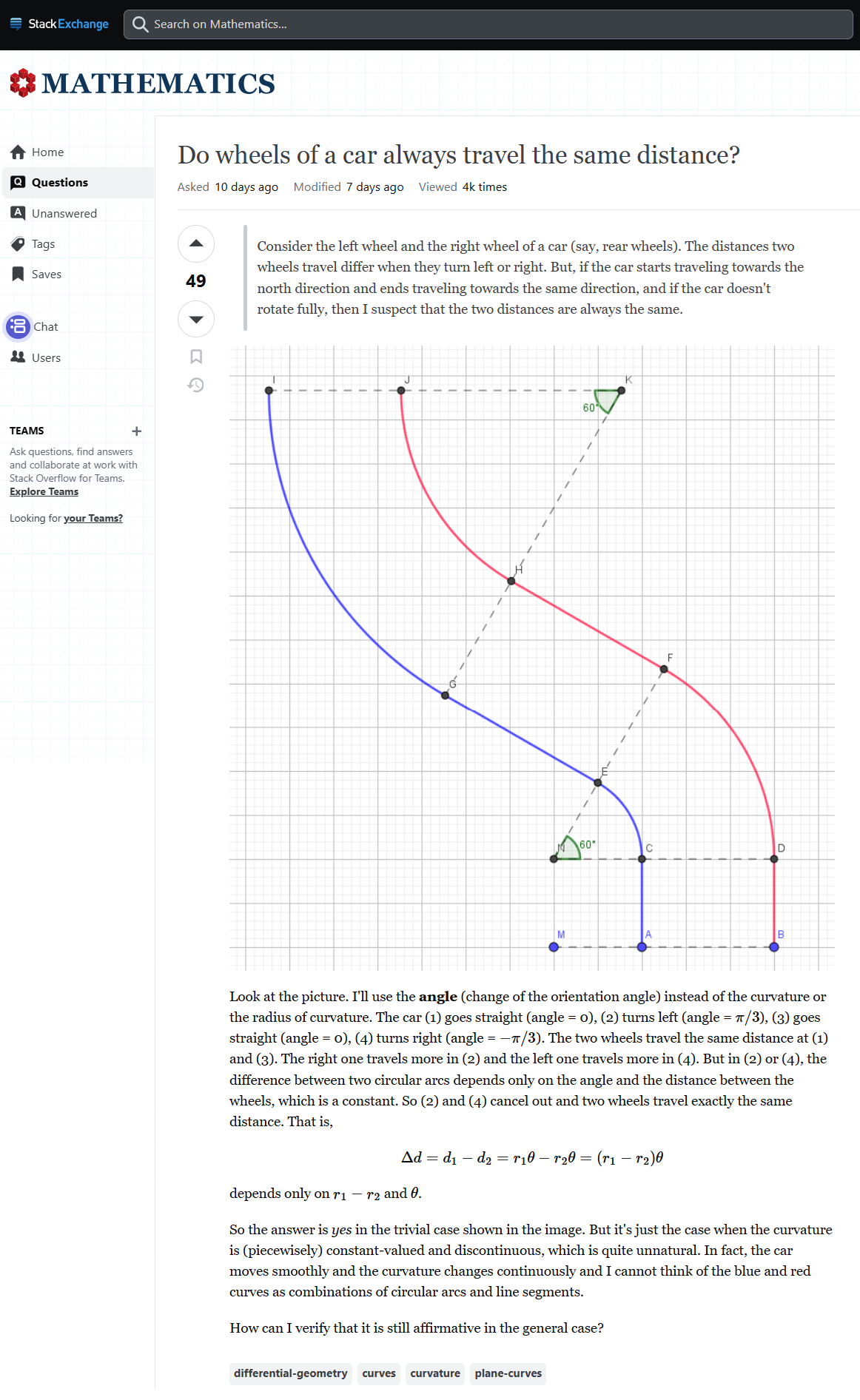
자동차의 두 뒷바퀴를 생각하자. 자동차가 좌회전하는 동안에는 왼바퀴보다 오른바퀴가 더 많은 거리를 이동할 것이고 우회전하는 동안에는 오른바퀴가 왼바퀴보다 더 많은 거리를 이동할 것이다. 하지만, 만약 자동차가 처음 향하던 방향과 마지막에 향하는 방향이 같다면, 그리고 한바퀴를 완전히 돌지 않았다면 두 바퀴가 이동한 총 거리는 같을 것이다.

1.1 간단한 예시 (trivial case)

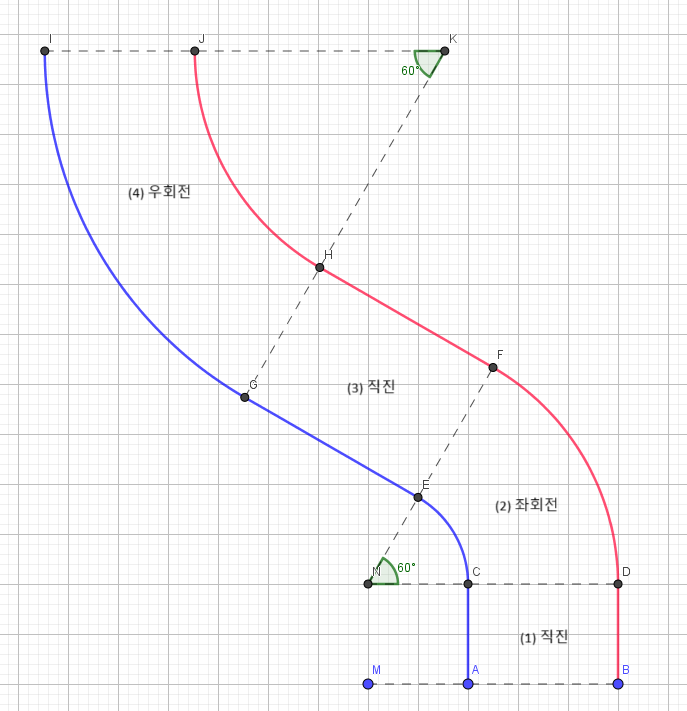
위 그림에서 파란 선은 왼바퀴의 궤적을, 빨간 선은 오른바퀴의 궤적을 나타낸다. 자동차는 (1) 직진하다가 (2) 60도만큼 좌회전하다가 (3) 다시 직진하다가 (4) 60도만큼 우회전한다. (1)과 (3)에서는 파란 선과 빨간 선의 길이가 당연히 같다. (2)에서는 빨간 선이 파란 선보다 더 길고 (4)에서는 파란 선이 빨간 선보다 더 길다. 하지만, (2)에서의 두 선의 길이의 차이가 (4)에서의 두 선의 길이의 차이가 같으므로 빨간 선과 파란 선의 전체 길이는 같게 된다. 이것은 차량이 회전할 때 두 선의 길이의 차이가 오로지 진행방향의 각도차이에만 의존하기 때문이다. 원글에서는

\[\Delta d = d_1-d_2=r_1\theta-r_2\theta=(r_1-r_2)\theta\]

라고 설명했고 이 설명으로도 충분하다고 생각된다. 하지만 좀 더 자세히 써보면 다음과 같다.

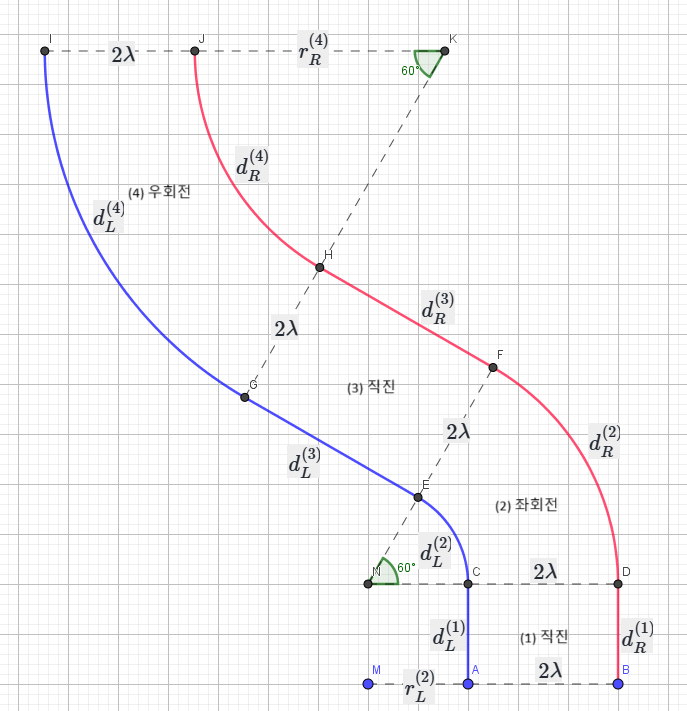
$k$번째 단계의 왼바퀴, 오른바퀴의 이동거리를 각각 $d_L^{(k)}$, $d_R^{(k)}$이라고 하자. 그러면 $d_L^{(1)}=d_R^{(1)}$이고 $d_L^{(3)}=d_R^{(3)}$이다. 각 바퀴의 이동거리는

\[\begin{align*} d_L&=d_L^{(1)}+d_L^{(2)}+d_L^{(3)}+d_L^{(4)}\\ d_R&=d_R^{(1)}+d_R^{(2)}+d_R^{(3)}+d_R^{(4)} \end{align*}\]

으로 쓰자.

$\Delta d^{(k)}=d_L^{(k)}-d_R^{(k)}$이라고 하면 $\Delta d^{(1)}=\Delta d^{(3)}=0$ 이고

\[\begin{align*} d_L-d_R &=\Delta d^{(1)}+\Delta d^{(2)}+\Delta d^{(3)}+\Delta d^{(4)}\\ &=\Delta d^{(2)}+\Delta d^{(4)}\\ \end{align*}\]

이 된다. 2단계와 4단계에서 각 바퀴는 일정한 곡률로 운동하고 있다. $k$단계의 왼바퀴, 오른바퀴의 곡률반지름을 각각 $r_L^{(k)}$, $r_R^{(k)}$이라고 하면, 곡률반지름의 차이는 두 바퀴 사이의 간격($=2\lambda$)으로 일정하다. 즉, $r_L^{(2)} \lt r_R^{(2)}$, $r_L^{(4)} \gt r_R^{(4)}$이고

\[r_R^{(2)}-r_L^{(2)}=r_L^{(4)}-r_R^{(4)}=2\lambda\]

이다. 그러면 ($\theta=\frac\pi3$)

\[\begin{align*} d_L-d_R &=\Delta d^{(2)}+\Delta d^{(4)}\\ &=d_L^{(2)} - d_R^{(2)} + d_L^{(4)} - d_R^{(4)}\\ &=r_L^{(2)}\theta - r_R^{(2)}\theta + r_L^{(4)}\theta - r_R^{(4)}\theta\\ &=\left(r_L^{(2)} - r_R^{(2)}\right)\theta + \left(r_L^{(4)} - r_R^{(4)}\right)\theta\\ &=-2\lambda\theta+2\lambda\theta\\ &=0 \end{align*}\]

인 것이다. 따라서 $d_L=d_R$이다.

1.2 예시 상황의 한계

이 예시는 문제를 떠올리는 계기를 만들어주었지만 계산을 편하게 하기 위해 매우 특수한 상황을 가정하고 있다. 운전자는 (1)에서는 자동차를 핸들을 정중앙에 놓고 운전하고 있고 (2)에서는 핸들을 일정 방향의 좌회전으로 돌린 채로 운전한다. 이것은 실제로는 불가능한 상황에 가깝다. (1)동안은 핸들이 정방향이다가 갑자기 (2)가 되는 순간 핸들이 돌아가져 있어야 한다. 즉, 핸들의 움직임이 불연속적이라는 것이고 곡률이 불연속적이라는 소리다. 이것이 실제 운전상황에서 가능하려면 (1)의 마지막 순간에 차량을 멈췄다가 핸들을 돌려 다시 운행하는 방식이면 가능하겠지만, 결코 일반적인 운동상황이라고는 생각할 수 없는 것이다. 실제로는 핸들, 즉 곡률과 곡률반지름이 적어도 연속적으로 (아마도 2차미분까지는 연속이 되도록) 변화할 것이다.

하지만, 또한 생각해보면, 예시 상황에서의 두 곡선의 길이가 같다면 곡률이 연속적으로 변하는 상황을 가정한다고 하더라도 여전히 두 곡선의 길이는 무한소의 상황에서도 잘 상쇄되어 같아지 않을까 하고 추정해볼 수 있을 것이다. 또한 만약 꼭 두 길이가 같지 않다면 어떤 경우에 같지 않은지도 생각해볼 수 있을 것이다.

1.3 수학적인 묘사

이 문제는 아주 실용적인 문제라 할 만하지만, 순수하게 수학적인 문제로 여길 수도 있다. 즉, 다음과 같은 문제로 치환될 수 있을 것이다.

폐구간 $I$에서 정의된 미분가능한 2차원 곡선 $\alpha:I\to\mathbb R^2$, $\beta:I\to\mathbb R^2$이 있다. 모든 $t\in I$에 대하여 $\left|\alpha’(t)\right|\gt0$, $\left|\beta’(t)\right|\gt0$이고 $\alpha’(t)\parallel\beta’(t)$이며 $\left|\alpha(t)-\beta(t)\right|=2\lambda$일 때, 다음이 성립합니다;

\[\int_I|\alpha(t)|\,dt=\int_I|\beta(t)|\,dt.\]

2. 풀이