직사각형 돌리기

2024-11-13 1 분 소요

어떤 독서모임에서 「로스할데」에 대해 소개했었는데 기다리다가 문득 다음과 같은 간단한 문제가 궁금해졌다.

1. 문제Permalink

$xy$ 평면 위에, 인접한 두 변의 길이가 $a$ , $b$ 인 직사각형 $R$ 이 있다고 하자. $R$ 의 양 변은 각 축과 할 필요는 없다. 이때 $R$ 의 최대 $x$ 값, 최소 $x$ 값, 최대 $y$ 값, 최소 $y$ 값을 통해 이루어지는 직사각형 $S$ 의 넓이는 언제 최대가 되며 그 최댓값은 얼마인가?

위 설명이 조금 descriptive한 설명이었다면, 조금 더 수식적인 설명은 다음과 같다.

직사각형 $R$ 에 대하여

S = {x : (x, y) \in R} \times {y : (x, y) \in R}

$S=\{x:(x,y)\in R\}\times\{y:(x,y)\in R\}$

일 때, $S$ 의 넓이의 최댓값을 구하여라.

말이 복잡하다. 그냥 그림으로 보면 쉽다.

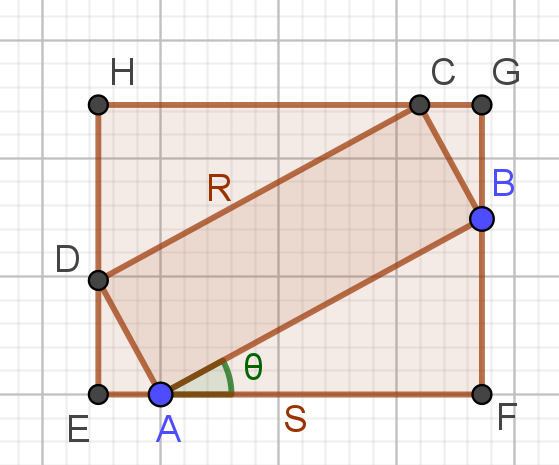
alt text

위 그림에서 직사각형 $R=\square ABCD$ 의 $x$ 축 기준으로의 최솟값이 $D$ 에서 최댓값이 $B$ 에서 발생하고, $y$ 축 기준으로의 최솟값이 $A$ 에서 최댓값이 $C$ 에서 발생하고 있으니, $B$ 와 $D$ 를 각각 지나는 수직선과 $A$ 와 $C$ 를 각각 지나는 수평선을 그어서 만들어지는 새로운 직사각형 $S=\square EFGH$ 를 생각했을 때, 이 $S$ 의 넓이는 언제 최대가 되며, 최댓값은 얼마인가?

2. 풀이Permalink

당연히, 문제는 각도 $\angle BAF$ 를 $\theta$ 로 두어 접근할 수 있고, 일반성을 잃지 않고 $0\le\theta\le\frac\pi2$ 라고 가정할 수 있다. 문제를 풀기 전에 생각해보면, 당연하게도 $\theta=\frac\pi4$ 인 경우에 최댓값이 되지 않을까, 하고 생각해볼 수 있다. 그럼 왜 그때 최대가 되며, 그 의미는 무엇일지.

주어진 $\theta$ 의 범위에서 $S$ 의 두 변의 길이는

\begin{aligned} E F & = x (B) - x (D) \\ E H & = y (C) - x (A) \end{aligned}

$\begin{align*} EF&=x(B)-x(D)\\ EH&=y(C)-x(A)\\ \end{align*}$

임이 명확하다. 그러면 ( $a=AD$ , $b=AB$ )

\begin{aligned} E F & = a \sin θ + b \cos θ \\ E H & = a \cos θ + b \sin θ \end{aligned}

$\begin{align*} EF&=a\sin\theta+b\cos\theta\\ EH&=a\cos\theta+b\sin\theta \end{align*}$

여서 문제는

A (θ) = (a \sin θ + b \cos θ) (a \cos θ + b \sin θ)

$A(\theta)=(a\sin\theta+b\cos\theta)(a\cos\theta+b\sin\theta)$

의 최댓값을 구하는 문제가 된다. 단순히 전개하면

\begin{aligned} A (θ) & = (a^{2} + b^{2}) \sin θ \cos θ + a b \sin^{2} θ + a b \cos^{2} θ \end{aligned}

$\begin{align*} A(\theta) &=(a^2+b^2)\sin\theta\cos\theta+ab\sin^2\theta+ab\cos^2\theta \end{align*}$

이고

\begin{aligned} A^{'} (θ) & = (a^{2} + b^{2}) (\cos^{2} θ - \sin^{2} θ) \\ = (a^{2} + b^{2}) (\cos θ - \sin θ) (\cos θ + \sin θ) \end{aligned}

$\begin{align*} A'(\theta) &=(a^2+b^2)(\cos^2\theta-\sin^2\theta)\\ &=(a^2+b^2)(\cos\theta-\sin\theta)(\cos\theta+\sin\theta) \end{align*}$

이다. $A’(\theta)=0$ 이 되는 유일한 $\theta$ 는 $\theta=\frac\pi4$ 가 되며 이때 극댓값을 가지므로 이것은 최댓값이기도 하다. 그 최댓값은

A (\frac{π}{4}) = \frac{1}{2} (a + b)^{2}

$A\left(\frac\pi4\right)=\frac12(a+b)^2$

이다.

어 문제가 너무 쉽게 풀리는데? 왜 나는 그당시에 $a$ 와 $b$ 에 대해 편미분하고 0으로 두었지. 이 문제를 $a$ 와 $b$ 에 대한 함수로 보는게 의미는 크게 없어보이는데.

3. 첨언Permalink

하지만, 마지막으로 한가지는 언급하고 넘어가자. $A(\theta)$ 는 삼각함수의 합성을 통해 재밌는 방식으로 표현될 수 있다.

각도 $\phi$ 를 ( $0\le\phi\lt2\pi$ )

\begin{aligned} \sin ϕ & = \frac{a}{\sqrt{a^{2} + b^{2}}} \\ \cos ϕ & = \frac{b}{\sqrt{a^{2} + b^{2}}} \end{aligned}

$\begin{align*} \sin\phi&=\frac a{\sqrt{a^2+b^2}}\\ \cos\phi&=\frac b{\sqrt{a^2+b^2}} \end{align*}$

를 만족시키는 각도라고 하자. 그러면

\begin{aligned} E F & = \sin θ \sin ϕ + \cos θ \cos ϕ \\ = \sqrt{a^{2} + b^{2}} \cos (θ - ϕ) \\ E H & = \cos θ \sin ϕ + \sin θ \cos ϕ \\ = \sqrt{a^{2} + b^{2}} \sin (θ + ϕ) \end{aligned}

$\begin{align*} EF &=\sin\theta\sin\phi+\cos\theta\cos\phi\\ &=\sqrt{a^2+b^2}\cos(\theta-\phi)\\ EH &=\cos\theta\sin\phi+\sin\theta\cos\phi\\ &=\sqrt{a^2+b^2}\sin(\theta+\phi) \end{align*}$

가 된다. 재밌는건, $\angle CAB$ 는 $\phi$ 와 같다고 볼 수 있으니까, 선분 $AC$ 와 각도 $\angle CAF$ 를 통해 보면 그림으로부터 $EH=\sqrt{a^2+b^2}\sin(\theta+\phi)$ 라는 식이 명확하다는 거다. $EF$ 도 마찬가지다.

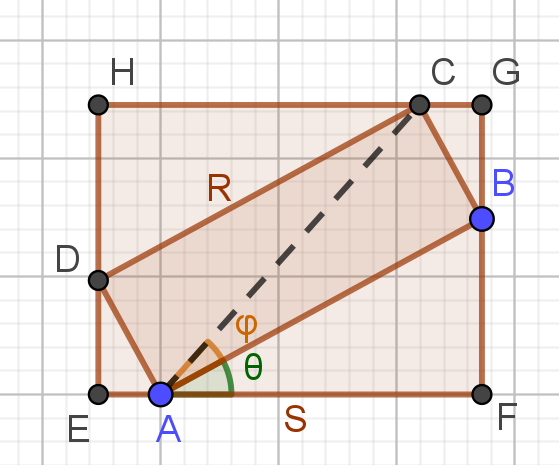
alt text

여하튼, 그러면

\begin{aligned} A (θ) & = (a^{2} + b^{2}) \sin (θ + ϕ) \cos (θ - ϕ) \\ = \frac{1}{2} (a^{2} + b^{2}) (\sin 2 θ + \sin 2 ϕ) \end{aligned}

$\begin{align*} A(\theta) &=(a^2+b^2)\sin(\theta+\phi)\cos(\theta-\phi)\\ &=\frac12(a^2+b^2)\left(\sin2\theta+\sin2\phi\right) \end{align*}$

이 된다. 그럼 $\theta=\frac\pi4$ 일 때 최대가 되는 게 당연하고 그때의 최댓값은

\begin{aligned} A (\frac{π}{4}) & = \frac{1}{2} (a^{2} + b^{2}) (1 + 2 \frac{a}{\sqrt{a^{2} + b^{2}}} \frac{b}{\sqrt{a^{2} + b^{2}}}) \\ = \frac{1}{2} (a^{2} + b^{2} + 2 a b) \\ = \frac{1}{2} (a + b)^{2} \end{aligned}

$\begin{align*} A\left(\frac\pi4\right) &=\frac12(a^2+b^2)\left(1+2\frac a{\sqrt{a^2+b^2}}\frac b{\sqrt{a^2+b^2}}\right)\\ &=\frac12(a^2+b^2+2ab)\\ &=\frac12(a+b)^2 \end{align*}$

이 되어 이전 결과와 일치한다.

P.S.Permalink

이 블로그의 단점 중 하나는, 최근 포스트만 너무 강조되어 표시된다는 거다. 아직 Fourier Analysis의 A1과 2단원의 내용을 다 쓰지 못했는데, 도중에 다른 글을 써버리면 이전 글이 묻혀버리는 것 같은 느낌이 들어 아쉽다.

1. 문제Permalink

2. 풀이Permalink

3. 첨언Permalink

P.S.Permalink

댓글남기기