확률론 : 1.3. 조건부확률과 독립 사건
1. 확률론 기초
확률론에 대한 기초적인 개념들에 대해 설명해봅니다. 흔히 고등학교 교과과정에서 하는 식으로, 경우의 수와 이항정리에 대해 먼저 다룹니다. 그 다음으로는 확률에 대하여 직관적인 방식과 엄밀한 방식으로 각각 설명해봅니다. 이후에는 조건부확률과 독립사건의 개념을 배운 후 Sterling’s lemma에 대해 간략히 살펴봅니다.
1.3. 조건부확률과 독립 사건
(1) 조건부확률
주사위를 던지는 시행에서 표본공간은
\[S=\{1,2,3,4,5,6\}\]이었습니다. 또한, $A$를 짝수가 나올 사건이라고 하면,
\[A=\{2,4,6\}\]이라고 쓸 수 있고 $P(A)$를
\[P(A)=\frac{n(A)}{n(S)}=\frac36=\frac12\]로 계산할 수 있다고 했었습니다. 한편, $B$를 3의 배수가 나올 사건이라고 하면
\[B=\{3,6\}\]이고
\[P(B)=\frac{n(B)}{n(S)}=\frac26=\frac13\]입니다.
이번 파트에서 생각하는 것은 “주사위를 한 번 던져서 짝수($A$)가 나왔다고 가정할 때, 그 눈이 3의 배수($B$)일 확률”입니다. 짝수가 나오는 경우가 2, 4, 6의 세 경우이고, 이 중 3의 배수가 6밖에 없으므로 그 확률은 $\frac13$으로 계산할 수 있을 것입니다. 즉,
\[P(B\mid A)=\frac{n(A\cap B)}{n(A)}=\frac{n(\{6\})}{n(\{2,4,6\})}=\frac13\]입니다. 이런 것을 조건부확률(conditional probability)이라고 하는데, 정확한 정의는 다음과 같습니다.
사건 $A$가 일어났다는 것을 가정했을 때 사건 $B$가 일어날 확률을 조건부확률이라고 부르고, $P(B\mid A)$로 적습니다. $P(B\mid A)$의 값은 $$P(B\mid A)=\frac{P(A\cap B)}{P(A)}$$ 으로 정의됩니다.
아까의 계산에서 사용한 정의
\[P(B\mid A)=\frac{n(A\cap B)}{n(A)}\]와 위의 정의는 일치합니다.
\[\frac{n(A\cap B)}{n(A)}=\frac{\frac{n(A\cap B)}{n(S)}}{\frac{n(A)}{n(S)}} = \frac{P(A\cap B)}{P(A)}\]이기 때문입니다.
$P(B\mid A)$를 계산했으니 반대로 $P(A\mid B)$도 계산해볼 수 있습니다. 이것은 “3의 배수($B$)가 나왔다고 가정할 때 그 눈이 짝수($A$)일 확률”입니다. 조건부확률의 정의에 의해
\[P(A\mid B)=\frac{P(A\cap B)}{P(B)}=\frac{\frac16}{\frac26}=\frac12\]입니다. 아니면
\[P(A\mid B)=\frac{n(A\cap B)}{n(B)}=\frac12\]와 같이 계산하여도 될 것입니다.
(2) 독립 사건
두 사건이 서로 영향을 미치지 않으면 두 사건을 독립(independent)이라고 합니다. 즉, 사건 $A$가 발생하는 것이 사건 $B$가 발생할 확률에 영향을 미치지 않는다면 (반대로, $B$가 $A$에 영향을 미치지 않는다면) 두 사건이 독립적이라고 말할 수 있을 것입니다. 다시 말하면, 사건 $B$가 발생할 확률과, 사건 $A$가 발생했을 때 사건 $B$가 발생할 확률과, 사건 $A$가 발생하지 않았을 때 사건 $B$가 발생할 확률이 모두 같으면 두 사건이 독립적이라고 말할 수 있습니다. 수식으로 쓰면
\[P(B)=P(B\mid A)=P(B\mid A^c)\]가 될 것입니다. 이것을 반대로 쓰면
\[P(A)=P(A\mid B)=P(A\mid B^c)\]입니다. 다시 말해, 총 4개의 식
\[\begin{align} P(B)&=P(B\mid A)\tag a\\ P(B)&=P(B\mid A^c)\tag b\\ P(A)&=P(A\mid B)\tag c\\ P(A)&=P(A\mid B^c)\tag d \end{align}\]이 성립하면 두 사건 $A$, $B$가 독립이라고 말할 수 있을 것입니다. 재미있는 것은 이 네 개의 식이 모두
\[P(A)P(B)=P(A\cap B)\tag e\]와 필요충분조건의 관계에 있다는 것입니다. 분모가 0이 되는 상황을 피하기 위해 $P(A)\ne0$, $P(B)\ne0$을 가정하고 각각을 증명해보겠습니다. 먼저 $\text{(e)}$의 양변을 $P(A)$로 나누면
\[P(B)=\frac{P(A\cap B)}{P(A)}=P(B\mid A)\]가 되어 $\text{(a)}$가 성립합니다. 반대로 $\text{(a)}$식의 양변에 $P(A)$를 곱하면 (e)가 됩니다. 따라서 $\text{(a)}\iff\text{(e)}$ 입니다. 마찬가지의 논리를 적용하면 $\text{(c)}\iff\text{(e)}$ 입니다. $\text{(b)}$에 관해서는
\[\begin{align*} \text{(b)} &\iff P(B)=P(B\mid A^c)\\[5pt] &\iff P(B)=\frac{P(B\cap A^c)}{P(A^c)}\\[5pt] &\iff P(B)P(A^c)=P(B\cap A^c)\\[5pt] &\iff P(B)(1-P(A))=P(B-A)\\[5pt] &\iff P(B)-P(A)P(B)=P(B)-P(A\cap B)\\[5pt] &\iff P(A)P(B)=P(A\cap B)\\[5pt] &\iff \text{(e)} \end{align*}\]이므로 $\text{(b)}\iff\text{(e)}$입니다. 또한, 마찬가지의 이유로 $\text{(d)}\iff\text{(e)}$ 입니다. $\square$
그러므로, 다음과 같이 독립의 개념을 정의할 수 있습니다.
$P(A)\ne0$, $P(B)\ne0$인 두 사건 $A$, $B$에 대하여 $$P(A\cap B)=P(A)P(B)$$ 이면 두 사건이 서로 독립이라고 말합니다. 한편, 두 사건이 서로 독립이 아니면, 두 사건이 서로 종속이라고 말합니다.
(3) 독립 사건 (예시)
예를 들어, (1)에서 $A$와 $B$는 독립입니다.
\[\begin{align*} A&=\{2,4,6\}\\ B&=\{3,6\} \end{align*}\]에서
\[P(A\cap B)=\frac16=\frac12\times\frac13=P(A)P(B)\]이기 때문입니다.
한편, $C$를 소수가 나올 사건이라고 하면
\[C=\{2,3,5\}\]이고,
\[P(A\cap C)=\frac16\ne\frac12\times\frac12=P(A)P(C)\]이므로 $A$와 $C$는 서로 종속이라는 것을 알 수 있습니다.
(4) 독립 사건의 해석
$A$와 $B$가 독립인 것은
\[\begin{align*} P(A)&=\frac36\\ P(A\mid B)&=\frac12\\ P(A\mid B^c)&=\frac24 \end{align*}\]가 되어
\[P(A)=P(A\mid B)=P(A\mid B^c)\]인 것을 통해서도 알 수 있습니다.
이와 같은 계산은 아래와 같이 표로 표현하면 쉽게 볼 수 있습니다. 가로축을 $A$에 속하는지 속하지 않는지, 세로축을 $B$에 속하는지 속하지 않는지로 나누어 4등분하고 각각에 원소의 갯수를 채워넣은 것입니다.

아래와 같이 빨간색 네모와 초록색 네모 부분을 살피면 $P(A\mid B)=\frac12$ 이고

$P(A\mid B^c)=\frac24$ 이며

$P(A)=\frac36$ 인 것을 확인할 수 있습니다.

다시 말해, 왼쪽열($A$)과 오른쪽열($A^c$)에 있는 숫자들의 갯수의 비율이 윗행($B$)과 아랫행($B^c$)과 관계없이 일정하면 독립인 것입니다.
마찬가지로, $P(B\mid A)=\frac13$ 이고

$P(B\mid A^c)=\frac13$ 이며

$P(B)=\frac26$ 이므로

인 것도 확인할 수 있습니다. 즉, 윗행($B$)과 아랫행($B^c$)에 있는 숫자들의 갯수의 비율이 왼쪽열($A$)과 오른쪽열($A^C$)에 상관없이 일정하므로 독립입니다.
한편, $A$와 $C$에 대해서도 표를 그려보면 다음과 같은데, 행과 열의 비율이 일정하지 않습니다. 왼쪽열($A$)과 오른쪽열($A^c$)에 있는 숫자들의 갯수의 비율이 윗행은 1:2이고 아랫행은 2:1입니다. 따라서 $A$와 $C$는 서로 종속이라고 생각해볼 수 있습니다.

실제로, $P(A\mid C)=\frac13$ 이고

$P(A\mid C^c)=\frac23$ 이며

$P(A)=\frac36$ 이므로

$A$와 $C$는 서로 독립이 아님을 확인할 수 있습니다.
(5) 독립과 배반
두 사건 $A$, $B$가 서로 독립인 것과 배반인 것은 완전히 별개의 문제입니다. 서로 독립이라고 배반이라고 할 수 없고, 서로 배반이라고 독립이라고 할 수도 없습니다.
예를 들어, 주사위를 하나 던지는 시행에서 $A=\{2,4,6\}$와 $B=\{3,6\}$는 서로 독립인 것을 아까 확인했지만, 서로 배반이라고는 할 수 없습니다.
또, 사건 $D$가 1이 나오는 경우를 가리킨다고 했을 때,
\[D=\{1\}\]인데, 그러면 $A$와 $D$는 서로 배반입니다. 하지만,
\[P(A\cap D)=0\ne\frac12\times\frac16=P(A)P(D)\]이므로 $A$와 $B$는 서로 독립이 아닙니다.
(6) 분할
사건들의 집합 $\mathcal A=\{A_i\mid i=1,2,\cdots,n\}$이 pairwisely exclusive이고, 다 합했을 때 전사건이 되면, $\mathcal A$를 $S$의 분할(partition)이라고 부릅니다. 다시 말해, 다음의 두 조건 (a), (b)을 만족시키면 됩니다 ;
\[\begin{align*} (a)~~&i\ne j\Longrightarrow A_i\cap A_j=\varnothing\\ (b)~~&A_1\cup A_2\cup\cdots\cup A_n=S \end{align*}\]$\mathcal A$의 정의에서 $i$는 임의의 index set의 원소여도 됩니다. 다시 말해, 공집합이 아닌 집합 $I$에 대하여 $\mathcal A=\{A_i\mid i\in I\}$가
\[\begin{align*} (a)~~&i\ne j\Longrightarrow A_i\cap A_j=\varnothing\\ (b)~~&\bigcup_{i\in I}A_i=S \end{align*}\]이면 $\mathcal A$는 $S$의 분할이라고 할 수 있습니다.
(7) 전확률의 정리
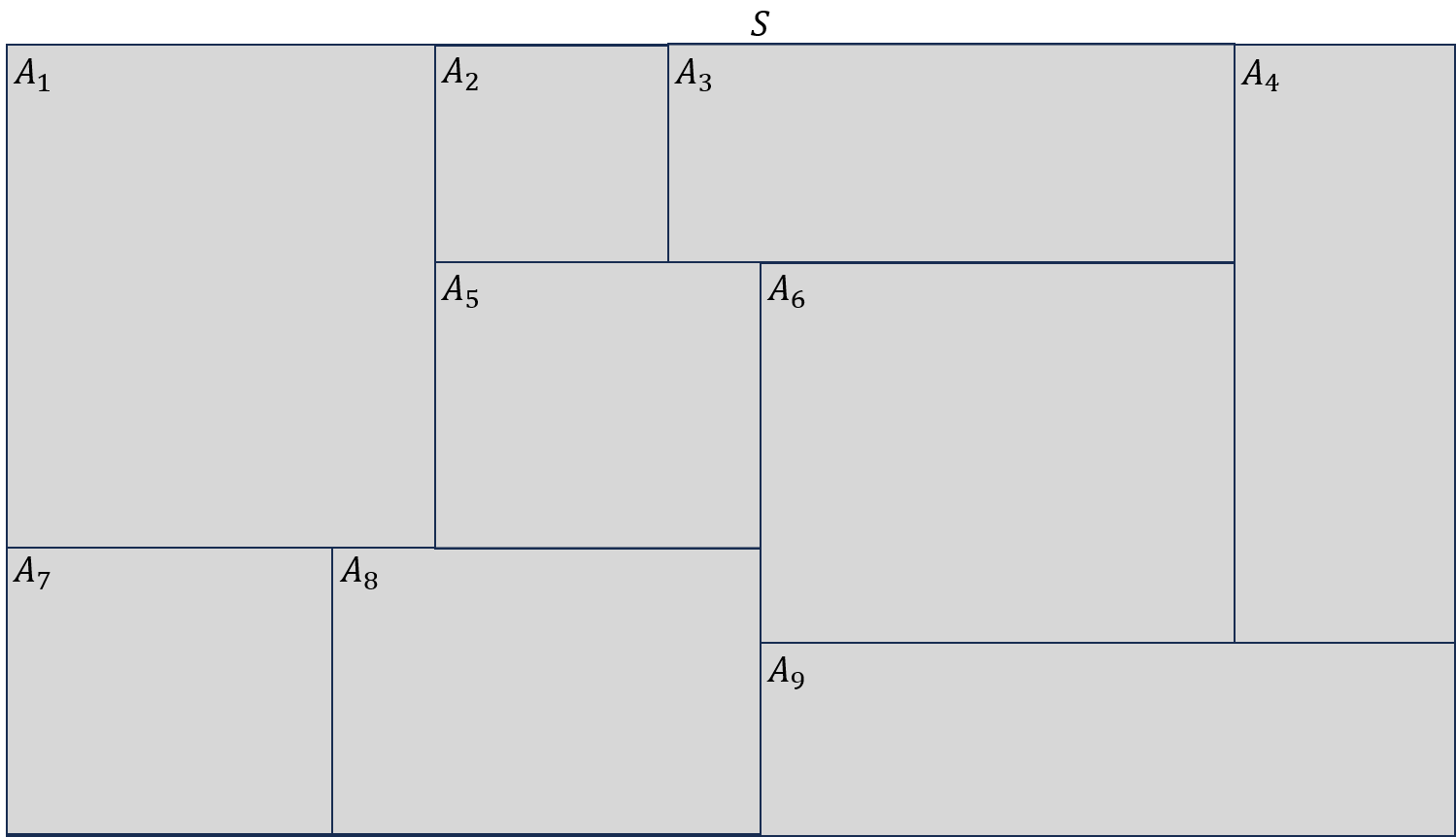
$\mathcal A=\{A_i\mid i=1,2,\cdots,n\}$가 $S$의 분할인 것은 그림으로 다음과 같이 나타낼 수 있을 것입니다.
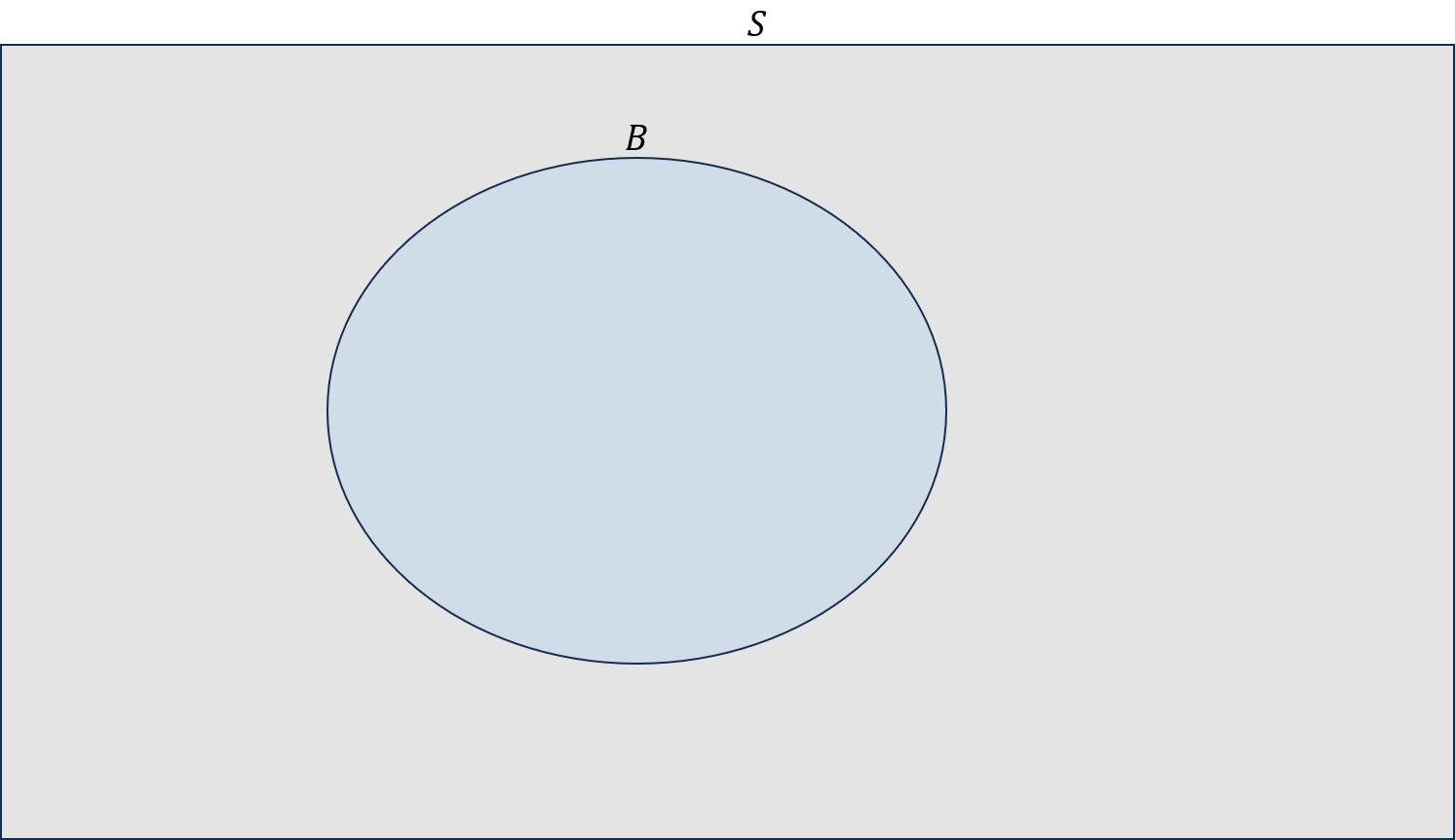
그리고 또다른 사건 $B$가 있다고 하겠습니다.
그러면, 아래 그림에서 $P(B)=P(A_1\cap B)+P(A_2\cap B)+\cdots+P(A_n\cap B)$임을 직관적으로 확인할 수 있습니다.
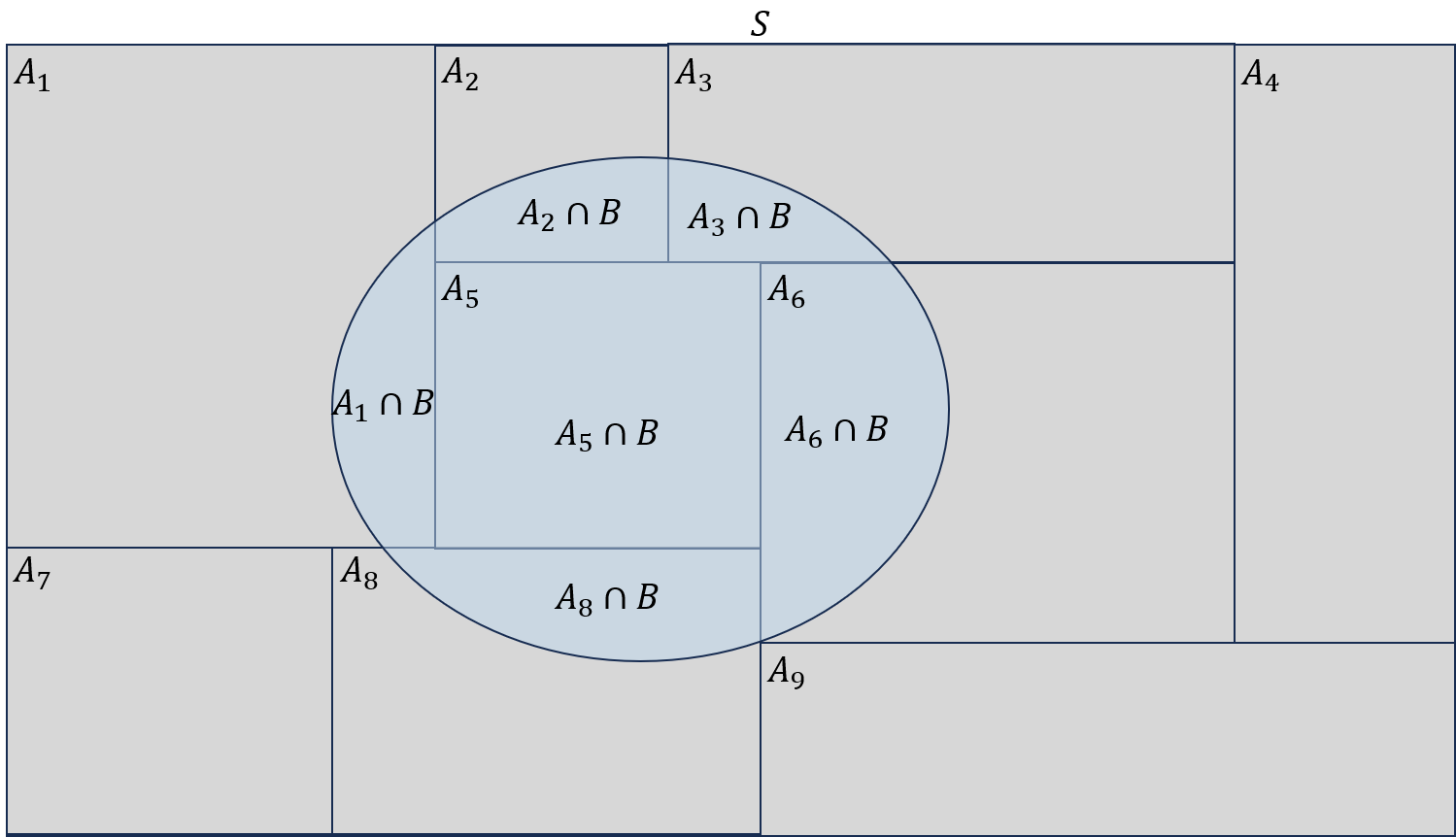
일반적으로, 다음의 전확률의 정리(law of total probability)가 성립합니다.
사건들의 집합 $\mathcal A=\\{A_i\mid i=1,2,\cdots,n\\}$가 $S$의 분할이고 $B$가 사건일 때, \begin{align*} P(B) &=\sum_{i=1}^nP(A_i\cap B)\\ &=\sum_{i=1}^nP(A_i)P(B\mid A_i) \end{align*}
이에 대한 증명은 집합의 분배법칙으로부터 간단히 나옵니다. 먼저,
\[\begin{align*} P(B) &=P(S\cap B)\\ &=P\left((A_1\cup A_2\cup\cdots\cup A_n)\cap B\right)\\ &=P\left((A_1\cap B)\cup(A_2\cap B)\cup\cdots\cup(A_n\cap B)\right)\\ &=P(A_1\cap B)+P(A_2\cap B)+\cdots+P(A_n\cap B) \end{align*}\]입니다. 따라서 첫번째 등식이 성립합니다. 또한, 조건부확률의 정의에서 $P(A_i\mid B)=\frac{P(A_i\cap B)}{P(B)}$으로부터 $P(A_i\cap B)=P(A_i)P(B\mid A_i)$가 성립하므로
\[\begin{align*} P(B) &=P(A_1\cap B)+P(A_2\cap B)+\cdots+P(A_n\cap B)\\ &=P(A_1)P(B\mid A_1)+P(A_2)P(B\mid A_2)+\cdots+P(A_n)P(B\mid A_n) \end{align*}\]이 성립합니다. $\square$
이상은 $\mathcal A$가 유한집합인 경우에 대한 설명이지만, $\mathcal A$가 countably infinte인 경우에도 비슷한 설명을할 수 있습니다. 즉, $\mathcal A={A_i\mid i=1,2,3,\cdots}$가 $S$의 분할이고 $B$가 사건일 때,
\[\begin{align*} P(B) &=\sum_{i=1}^\infty P(A_i\cap B)\\ &=\sum_{i=1}^\infty P(A_i)P(B\mid A_i) \end{align*}\]가 성립합니다.
(8) 전확률의 정리 (예시)
다음과 같은 문제를 풀어봅시다. 각각 5개의 구슬이 담겨있는 세 종류의 자루가 있습니다.
- 첫번째 자루에는 4개의 빨간 구슬과 1개의 파란 구슬이 담겨있습니다.
- 두번째 자루에는 2개의 빨간 구슬과 3개의 파란 구슬이 담겨있습니다.
- 세번째 자루에는 5개의 파란 구슬이 담겨있습니다.
임의로 자루를 하나 택한 뒤 자루 속에서 구슬을 하나 꺼낼 때, 빨간 구슬이 나올 확률은 얼마일까요?
쉬운 문제이지만, 앞서 설명한 개념들을 활용해서 풀어보겠습니다. 표본공간 $S$는 $S=\{1,2,3\}\times\{1,2,3,4,5\}$로 나타낼 수 있습니다. 즉,
\[\begin{align*} S =\{&1,2,3\}\times\{1,2,3,4,5\}\\ =\{&(1,1), (1,2), (1,3), (1,4), (1,5),\\ &(2,1), (2,2), (2,3), (2,4), (2,5),\\ &(3,1), (3,2), (3,3), (3,4), (3,5)\} \end{align*}\]입니다. 각각의 근원사건 $(i,j)$는 $i$번째 자루를 선택한 뒤 $j$번째 구슬을 선택하는 상황을 나타냅니다. 총 15개의 근원사건들 중, 빨간구슬이 택해지는 경우는 첫번째 자루를 택했을 때의 4개의 경우, 두번째 자루를 택했을 때의 2개의 경우이므로, 구하는 확률은 $\frac{2+4}{15}=\frac25$이 될 것입니다.
이것을 전확률의 정리로 풀어보겠습니다. 사건 $A_1$, $A_2$, $A_3$를 각각 첫번재 자루, 두번째 자루, 세번째 자루를 선택하는 사건이라고 하겠습니다. 수학적으로 표현하면
\[\begin{align*} A_1&=\{1\}\times\{1,2,3,4,5\}=\{(1,1), (1,2), (1,3), (1,4), (1,5)\}\\ A_2&=\{2\}\times\{1,2,3,4,5\}=\{(2,1), (2,2), (2,3), (2,4), (2,5)\}\\ A_3&=\{3\}\times\{1,2,3,4,5\}=\{(3,1), (3,2), (3,3), (3,4), (3,5)\} \end{align*}\]입니다. 그러면 $\{A_1,A_2,A_3\}$은 $S$의 분할이 됩니다.
사건 $R$을 빨간 구슬을 선택하는 사건이라고 하면 전확률의 정리에 의해
\[\begin{align*} P(R) &=P(A_1\cap R)+P(A_2\cap R)+P(A_3\cap R)\\ &=P(A_1)P(R\mid A_1)+P(A_2)P(R\mid A_2)+P(A_3)P(R\mid A_3)\\ &=\frac13\times\frac45+\frac13\times\frac25+\frac13\times0\\ &=\frac{4+2}{15}\\ &=\frac25 \end{align*}\]가 됩니다.
참고한 자료
댓글남기기