M/M/1 Queue

0. Overview

\(\mathbb E[K] = \frac\rho{1-\rho}\tag{1}\)

학부에 다니면서는 확률 공부를 아예 하지 않았고, 대학원에 있으면서는 확률을 다루기는 했지만 큐잉이론은 공부할 일은 없었습니다. 다만, 이 분야를 전공하시는 교수님이 계셨기 때문에 queueing theory 라는 이름 자체에는 익숙했고, 대충 무슨 것을 하는 지는 알고 있었습니다. 그러다 작년, 확률론 일반을 공부하면서 Poisson process를 배우게 되었고, 그때 배웠던 것이 이번에 M/M/1 대기행렬 이론을 이해하는 데 큰 도움이 되었습니다.

주로 공부한 자료는 다음의 유튜브 영상입니다.

• Queueing theory and Poisson process

워낙 유튜브 영상에서 완벽하고 친절하게 M/M/1 queueing theory에 대해 설명하고 있어서, 별도로 포스팅을 하는 게 의미가 있을까 싶을 정도입니다. 하지만, 공부한 기록을 남기고 싶기도 하고, 해당 영상에서는 $\mathbb E[K]$ 식에 대한 증명까지는 하고 있지 않으므로, 포스팅을 남겨봅니다.

$\mathbb E[K]$ 식에 대한 증명은

• Expected waiting time in M/M/1 queue

를 보고 해봤지만, 해당 글에 증명이 직접적으로 있지는 않습니다.

모든 논의는 Poisson process를 기반으로 합니다. Poisson process에 대해서는 어느 정도 알고 있다고 자부했지만, 막상 글을 쓰려니 확실히 설명하기가 어려웠습니다. 위키피디아에 개략적인 설명이 있고 University of Münster 자료에서는 axiomatic한 정의를 찾았지만,

• Chapter2 : Poisson Processes (MIT 자료)

가 가장 잘 설명되어 있기에 많이 참고했습니다.

1. Poisson Process

카페를 운영하고 있는 사장님이 손님을 기다리고 있습니다. 만약 10분에 한 명 꼴로 손님이 들어온다고 하면 손님이 카페에 들어오는 과정은 Poisson process로 모델링될 수 있습니다.

배달기사가 배달주문을 기다리고 있습니다. 1시간에 5번 꼴로 배달주문이 접수된다고 하면, 몇 분 후에 배달 일이 잡힐 지 하는 것도 Poisson process로 모델링될 수 있습니다.

방사성 물질에서 방사선이 방출됩니다. 방출되는 방사선의 양 또한 Poisson process으로 모델링될 수 있습니다.

이렇듯, 많은 자연현상 혹은 사회현상들이 Poisson process으로 해석될 수 있습니다. 정확하게는, 어떤 사건이 시간에 따라 반복적으로 일어날 수 있고, 사건이 일어날 것이라고 기대되는 정도가 이전의 사건 발생에 관계없이 일정하다고 가정될 때, Poisson process를 생각할 수 있습니다.

확률론에서 '사건(event)'이라는 말은 표본공간의 부분집합을 의미합니다. 하지만 이 글에서는 특정한 일이 발생하는 것을 '사건(arrival)'이라고 썼습니다. 이것은 MIT 자료에서 두 개념 사이의 모호성을 방지하기 위해 event라는 단어 대신 arrival이라는 단어를 사용한 데 따른 것입니다. 이런 관점에서 '사건'이라는 단어는 event가 아닌 arrival을 지칭합니다.

1.1 stochastic process

확률변수들의 집합(a collection of random variables)을 확률과정(stochastic process)라고 합니다. 즉, 공집합이 아닌 집합 $J$(index set)이 존재해서 모든 $j\in J$에 대하여 $X_j$가 확률변수이면

\[\{X_j:j\in J\}\]

를 확률과정이라고 합니다.

1.2 arrival process

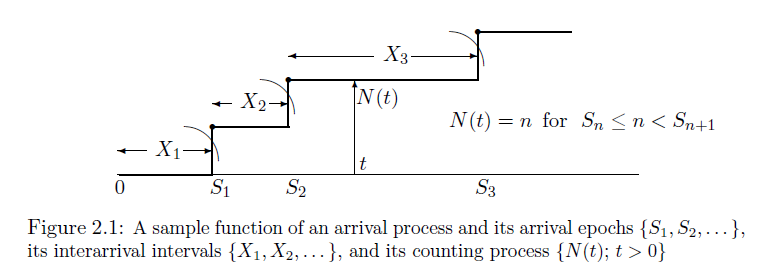
어떤 사건(arrival)이 시간 $t\ge0$에 따라 반복적으로 일어나면 이것을 arrival process라고 부릅니다. 만약 사건이 시각 $S_1$, $S_2$, $S_3$, $\cdots$ 에서 일어난다면 ($S_1<S_2<S_3<\cdots$) 다음과 같은 그림으로 arrival process의 상황을 표현할 수 있습니다.

사건이 일어나는 시점 $S_i$가 일정하게 결정되어 있지 않고 확률적으로 발생한다면, 각각의 실수 $S_i$는 확률변수로 해석될 수 있습니다. 따라서 arrival process는 확률과정

\[\{S_i:i=1,2,3,\cdots\}\tag{2}\]

으로 표현될 수 있습니다. 이때의 index set은 자연수 집합입니다.

한편, 인접한 두 사건의 시간간격을 $X_i$라고 하면, 다시 말해

\[X_i= \begin{cases} S_i-S_{i-1} &(i>1)\\ S_1 &(i=1) \end{cases}\]

라고 하면, 그림으로는

로 표현할 수 있을 것입니다. 그러면 $X_i$들도 확률변수라고 말할 수 있으므로 arrival process는 확률과정

\[\{X_i:i=1,2,3,\cdots\}\tag{3}\]

으로도 표현될 수도 있습니다.

또한, 특정한 시점 $t\ge0$에 대하여, 시각 $t$까지 사건이 발생한 횟수를 $N_t$라고 하면

$N_t$는 확률변수입니다. 따라서 arrival process는 확률과정

\[\{N_t:t\ge0\}\tag{4}\]

으로도 표현될 수 있습니다. 이때의 index set은 0보다 크거나 같은 실수들의 집합입니다. 즉, 위의 그림에서는 편의상 $t$가 자연수인 경우만을 나타냈는데, 임의의 양수 $t$에 대하여 확률변수 $N_t$를 생각할 수 있습니다.

다시 말해, arrival process는 확률과정의 일종인데, (2), (3), (4)의 서로 다른 세 방식의 확률변수로 나타낼 수 있습니다.

1.3 renewal process

만약 각 arrival의 발생이 서로 독립적이고 각 arrival의 발생조건이 일정하다면 문제 상황을 조금 더 간결하게 만들 수 있습니다.

$X_i$들이 서로 독립적이면서 확률분포가 일정한 (IID, independent and identically distributed) arrival process를 renewal process라고 부릅니다.

1.4 Poisson process

모든 $i$에 대하여 $X_i$의 PDF가

\[f_{X_i}(x)=\lambda e^{-\lambda x}\quad(x\ge0)\]

로 일정하게 주어지는 renewal process를 Poisson process라고 부릅니다. 이때, $\lambda\gt0$는 상수입니다. 이 분포를 지수분포(exponential distribution)라고 부르므로, Poisson process는 사건이 일어나는 시간의 간격이 지수분포를 이루는 경우를 말한다고 할 수 있습니다.

1.5 exponential distribution

Poisson process에서의 시간간격 $X_i$는 지수분포를 따른다고 했었습니다. 이때, 지수분포란, $X\ge0$에서 정의되는 연속확률분포로서

\[f_X(x)=\lambda e^{-\lambda x}\quad(x\ge0)\tag{5}\]

와 같은 PDF를 가지는 분포를 말합니다.

여기에서는 지수분포에 대한 기본적인 계산을 해봅니다. 먼저, $X$의 전체 확률은 1로 계산됩니다.

\[\begin{align*} P(X\ge0) &=\int_0^\infty f_X(x)\,dx\\ &=\int_0^\infty\lambda e^{-\lambda x}\,dx\\ &=\left[-e^{-\lambda x}\right]_0^\infty\\ &=0-(-1)\\ &=1 \end{align*}\]

$X$의 CDF를 구해보면

\[\begin{align*} F_X(x) &=P(X\le x)\\ &=\int_0^xf_X(x)\,dx\\ &=\int_0^x\lambda e^{-\lambda x}\,dx\\ &=\left[-e^{-\lambda x}\right]_0^x\\ &=(-e^{-\lambda x})-(-1)\\ &=1-e^{-\lambda x} \end{align*} \tag{6}\]

이 됩니다. $X$의 평균을 구해보면

\[\begin{align*} \mathbb E[X] &=\int_0^\infty xf_X(x)\,dx\\ &=\int_0^\infty x\lambda e^{-\lambda x}\,dx\\ &=\left[-xe^{-\lambda x}\right]_0^\infty + \int_0^\infty e^{-\lambda x}\,dx\\ &=\left[(-0) - (-0)\right] + \left[-\frac1\lambda e^{-\lambda x}\right]_0^\infty\\ &=(-0)-\left(-\frac1\lambda\right)\\ &=\frac1\lambda \tag{7} \end{align*}\]

이 됩니다.

따라서, Poisson process에서 arrival이 발생하는 시간간격의 평균은 $\frac1\lambda$이고, $\lambda$는 arrival이 발생하는 평균빈도를 나타냅니다.

1.6 memoryless property

지수분포는 memoryless property라는 중요한 성질을 가집니다.

$X$가 연속확률변수일 때, 임의의 두 양수 $x_1$, $x_2$에 대하여 다음이 성립하면 $X$가 memoryless property를 가진다고 말합니다;

\[\begin{align*} P(X\gt x_1+x_2\vert X\gt x_2) = P(X\gt x_1) \end{align*} \tag{8}\]

$X\gt x$는 $x$의 시간동안 사건이 발생하지 않았음을 의미합니다. 따라서, 위 식의 좌변은 $x_2$의 시간동안 사건이 발생하지 않았을 때, $x_1+x_2$의 시간동안 사건이 발생하지 않았음을 의미합니다. 그러면 위 식은 $x_2$의 시간동안 사건이 발생하지 않았다고 가정할 때, 그다음 $x_1$만큼의 시간동안 사건이 발생하지 않을 확률이, ($x_2$의 시간동안 사건이 발생하지 않았다는 가정 없이) $x_1$의 시간동안 사건이 발생하지 않을 확률과 같다는 것을 뜻합니다. 즉, 이전에 사건이 발생했건 발생하지 않았건 상관없이, 앞으로 $x_1$만큼의 시간동안 사건이 일어날 확률은 일정하다는 것입니다.

식 (8)은 조건부확률의 정의에 의해 다음 식과 동치입니다 ;

\[P(X\gt x_1+x_2)=P(X\gt x_1)P(X\gt x_2)\]

그리고 이 식은 식 (6)에 의해 쉽게 증명됩니다;

\[\begin{align*} P(X\gt x_1)P(X\gt x_2) &=\left(1-F_X(x_1)\right)\left(1-F_X(x_2)\right)\\ &\stackrel{(6)}=e^{-\lambda x_1}e^{-\lambda x_2}\\ &=e^{-\lambda(x_1+x_2)}\\ &\stackrel{(6)}=1-F_X(x_1+x_2)\\ &=P(X\gt x_1+x_2) \end{align*}\]

흥미로운 것은, memoryless property를 가지는 유일한 연속확률분포가 지수분포라는 것입니다. 이에 대한 증명을 위해 연속확률변수 $X$가 memoryless property (8)을 가진다고 가정하고 $h(x)=\ln P(X\gt x)$로 두면,

\[\begin{align*} h(x_1+x_2) &=\ln P(X\gt x_1+x_2)\\ &=\ln P(X\gt x_1)P(X\gt x_2)\\ &=\ln P(X\gt x_1) + \ln P(X\gt x_2)\\ &=h(x_1)+h(x_2) \tag{9} \end{align*}\]

이 성립합니다.

확률변수 $X$가 음이 아닌 실수인 경우만을 고려합니다. 즉, $P(X\lt0)=0$인 상황을 가정합니다. 따라서 함수 $h(x)=\ln P(X\gt x)$에서 $x$의 범위는 $x\ge0$ 입니다.

그러면 수학적 귀납법에 의해서, 자연수 $n$에 대하여

\[h(nx) = h(x+x+\cdots+x)=h(x)+h(x)+\cdots+h(x)=nh(x)\]

입니다. 그러면, 자연수 $m$에 대하여

\[mh\left(\frac1mx\right)=h(x)\]

이 성립하고 이 식의 양변을 $m$으로 나누면

\[h\left(\frac1mx\right)=\frac1mh(x)\]

가 됩니다. 따라서 유리수 $q=\frac nm\gt0$에 대하여

\[h(qx)=h\left(n\cdot\frac1mx\right)=nh\left(\frac 1mx\right)=n\cdot\frac1mxh(x) = qh(x)\]

입니다. 마지막으로 극한의 개념을 적절히 사용하면 실수 $c\gt0$에 대하여

\[h(cx)=ch(x)\tag{10}\]

임을 증명할 수 있습니다. 식 (9)과 (10)에 의해, $h(x)$는 선형함수이고, 따라서

\[h(x)=\ln P(X\gt x)=kx\]

인 실수 $k$가 존재합니다. $0\lt P(X\gt x)\lt1$ 에서 $k\lt0$이므로 $k=-\lambda$로 두면 ($\lambda\gt0$)

\[P(X\gt x)=e^{-\lambda x}\]

가 성립합니다. 그러면

\[F_X(x) = 1-e^{-\lambda x}\]

이고 미분을 통해

\[f_X(x)=\lambda e^{-\lambda x}\]

를 얻을 수 있습니다. 따라서, memoryless property를 가지는 유일한 연속확률분포는 지수분포임을 확인할 수 있습니다. $\square$

1.7 Poisson distribution

Poisson process는 $X_i$가 지수분포를 따르는 경우를 말한다고 했습니다. 그런데 Poisson process는 세 종류의 확률변수 $S_i$, $X_i$, $N_t$로 표현될 수 있다고 했으므로, Poisson process의 상황은 다른 확률변수 $S_i$, $N_t$로도 묘사될 수 있습니다. 특히 $N_t$로 묘사될 수 있습니다. $t=1$인 경우, 그러니까 $N_1$은 하나의 확률변수인데, $N_1$의 분포를 Poisson distribution이라고 합니다. 이것은 단위시간동안의 arrival의 횟수의 분포를 의미합니다. 이 절에서는 간단히 $N=N_1$으로 쓰겠습니다.

(7)에서 평균적으로 $\frac1\lambda$만큼의 시간간격마다 arrival이 발생한다고 했었습니다. 따라서, ‘단위시간마다 평균적으로 $\lambda$번의 arrival이 발생’합니다.

이때, 단위시간간격을 $m$개의 짧은 시간간격(subinterval) $\left[\frac{k-1}m, \frac km\right]$으로 나누게되면($k=1,2,\cdots,m$), 각 subinterval마다 평균적으로 $\frac\lambda m$번의 arrival이 발생하리라고 기대할 수 있습니다.

충분히 큰 $m$을 생각하면, subinterval 동안 두 번 이상의 arrival이 발생하지 않으리라고 가정할 수 있습니다. 다시 말해, 해당 subinterval에서의 arrival이 발생한 횟수를 $N^{(k)}$라고 하면, $N^{(k)}$는 0 또는 1입니다. 그리고 $N^{(k)}$의 기댓값이 $\frac\lambda m$이라고 했으므로, $N^{(k)}\sim\text{Bernoulli}(\frac\lambda m)$입니다. 그러면, 단위시간동안의 arrival의 횟수 $N$은

\[N=N^{(1)}+\cdots+N^{(n)}\]

이고, 각각의 subinterval에서의 베르누이 시행이 독립적이라고 가정할 수 있으므로, $N$의 분포는 독립시행의 확률로 특정될 수 있습니다 ;

\[P(N=n)=\binom mn\left(\frac\lambda m\right)^n\left(1-\frac\lambda m\right)^{m-n}\quad(n=0,1,2,\cdots,m)\]

이 식은 $m$이 충분히 크다는 가정하에서만 성립합니다. 따라서, $m$을 무한대로 보내서 $P(N=n)$를 정확하게 구하면

\[\begin{align*} P(N=n) &=\lim_{m\to\infty}\binom mn\left(\frac\lambda m\right)^n\left(1-\frac\lambda m\right)^{m-n}\\ &=\lim_{m\to\infty}\frac{m(m-1)\cdots(m-n+1)}{n!}\left(\frac\lambda m\right)^n\left(1-\frac\lambda m\right)^{m-n}\\ &=\lim_{m\to\infty}\frac{m(m-1)\cdots(m-n+1)}{m^n}\left(\frac{\lambda^n}{n!}\right)\left(1-\frac\lambda m\right)^{m-n}\\ &=\frac{\lambda^n}{n!}\lim_{m\to\infty}1\frac{m-1}m\cdots\frac{m-n+1}m\lim_{m\to\infty}\left(1-\frac\lambda m\right)^{m-n}\\ &=\frac{\lambda^n}{n!}\lim_{m\to\infty}\left(1-\frac\lambda m\right)^{-n}\lim_{m\to\infty}\left(1-\frac\lambda m\right)^m\\ &=\frac{\lambda^n}{n!}\lim_{m\to\infty}\left(\left(1-\frac\lambda m\right)^{-\frac m\lambda}\right)^{-\lambda}\\ &=\frac{\lambda^n}{n!}e^{-\lambda}\\ \end{align*}\]

입니다. 정리하면

\[P(N=n)=\frac{\lambda^n}{n!}e^{-\lambda}\quad(n=0,1,2,\cdots)\tag{11}\]

입니다. 이것이 Poisson distribution의 PMF입니다.

Poisson distribution에 대하여 간단한 계산을 해보겠습니다. 가능한 모든 $n$에 대한 확률을 더하면 1이 됩니다 ;

\[\begin{align*} \sum_{n=0}^\infty P(N=n) &=\sum_{n=0}^\infty\frac{\lambda^n}{n!}e^{-\lambda}\\ &=e^{-\lambda}\sum_{n=0}^\infty\frac{\lambda^n}{n!}\\ &\stackrel{(\ast)}=e^{-\lambda}e^\lambda\\ &=1 \end{align*}\]

$(\ast)$에서 지수함수에 대한 Taylor(Maclaurin) series를 사용했습니다. 이번에는 확률변수 $N$의 평균을 구해보면

\[\begin{align*} \mathbb E[N] &=\sum_{n=0}^\infty nP(N=n)\\ &=\sum_{n=0}^\infty n\times\frac{\lambda^n}{n!}e^{-\lambda}\\ &=\sum_{n=1}^\infty n\times\frac{\lambda^n}{n!}e^{-\lambda}\\ &=\lambda e^{-\lambda}\sum_{n=1}^\infty \frac{\lambda^{n-1}}{(n-1)!}\\ &=\lambda e^{-\lambda}\sum_{n'=0}^\infty \frac{\lambda^{n'}}{n'!}\\ &=\lambda e^{-\lambda}\times e^\lambda\\ &=\lambda \end{align*}\]

이 됩니다. 따라서 ‘단위시간마다 평균적으로 $\lambda$번의 arrival이 발생’한다는 사실이 이 계산으로 재확인된 셈입니다.

어떤 arrival이 시간에 따라 독립적으로, 그리고 동일한 확률조건에 따라 발생하는 상황을 Poisson process라고 한다고 했습니다. 그리고 여기서 말하는 arrival은 '도착'이라기보다는 일반적인 '사건'을 의미합니다. 즉, '카페에 손님이 들어오는 사건', '배달 주문이 접수되는 사건', '방사성 물질에서 방사선이 방출되는 사건' 같은 것을 의미합니다.

2. M/M/1 queue

카페에 손님이 들어오면 손님은 키오스크를 통해 음료를 주문합니다. 키오스크는 한 대밖에 없고, 따라서 첫번째 손님이 주문을 하는 도중에 두번째 손님이 들어오면 두번째 손님은 첫번째 손님 뒤에 줄을 서게 됩니다. 손님이 더 들어오면 줄은 길어질 것이고, 앞 손님이 주문을 마쳐서 줄에서 빠져나가면 줄은 짧아질 겁니다. 만약 손님이 카페에 들어오는 사건과 주문을 마치는 사건이 어떤 조건에 의해 발생하는지 알 수 있다면 손님들이 서있는 줄의 길이에 대한 확률분포를 계산하는 데 사용될 수 있을 겁니다.

총 100대의 차량을 수용할 수 있는 주차장이 있습니다. 이 주차장에는 현재 80대의 차량이 주차되어 있습니다. 주차장에는 입구와 출구가 각각 하나씩 있는데, 입구에서는 한시간에 열 대 꼴로 차가 들어오고 있고, 출구에서는 한시간에 여섯 대 꼴로 차가 나가고 있습니다. 시간이 지날 수록 주차장에 주차된 차량의 대수는 점점 많아지는 경향을 보이다가, 다섯 시간 후에는 주차장이 꽉 찰 것이라고 예상할 수 있습니다. 어떤 시점 $t$에 주차장에 주차되어 있는 차량의 대수를 $K_t$라고 할 때, $K_t$에 대한 분포를 계산해보는 문제를 생각할 수 있습니다.

위의 두 사례는 M/M/1 queue를 사용하여 기술될 수 있습니다.

2.1 queue

queue란, job과 server로 이루어진 어떤 대상을 의미합니다. server는 job을 받아서 처리하는 일을 반복합니다. server가 job을 받는 것을 arrival이라고 하고, 처리하는 것을 departure이라고 합니다.

위의 첫번째 사례에서는 job, server, arrival, departure가 다음과 같습니다.

• job : 음료 주문 (또는 손님)
• server : 키오스크
• arrival : 손님이 카페에 들어와서 줄을 서는 것
• departure : 음료를 주문하는 것을 마치고 줄에서 빠져나가는 것

두번째 사례에서는

• job : 주차 (또는 자동차)
• server : 주차장
• arrival : 차량이 주차장 입구로 들어오는 것
• departure : 차량이 주차장 출구로 빠져나가는 것

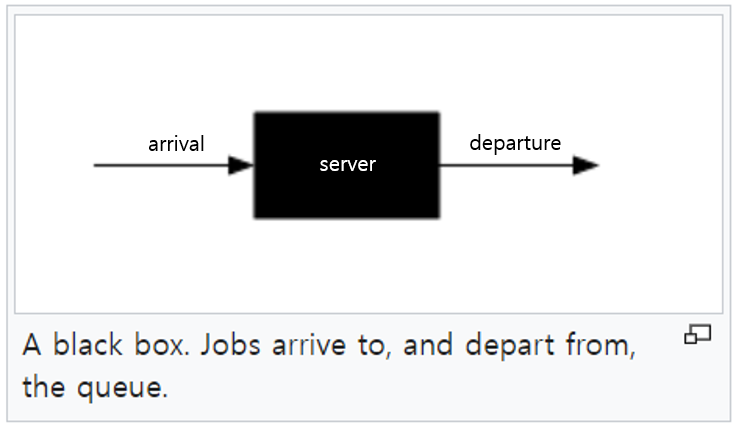
위키피디아에서는 queue의 개념을 다음과 같이 설명하고 있습니다.

A queue or queueing node can be thought of as nearly a black box. Jobs (also called customers or requests, depending on the field) arrive to the queue, possibly wait some time, take some time being processed, and then depart from the queue.

2.2 M/M/1 queue

설명한 두 사례에서는 server가 한 개였습니다. 하지만 server는 여러 개 있을 수도 있습니다. 예를 들어, 카페 안에 키오스크가 여러 대 있을 수 있고, 주차장 건물도 두 동이 있을 수 있습니다. 아래 그림은 세 개의 server가 존재하는 queueing system을 나타내고 있습니다.

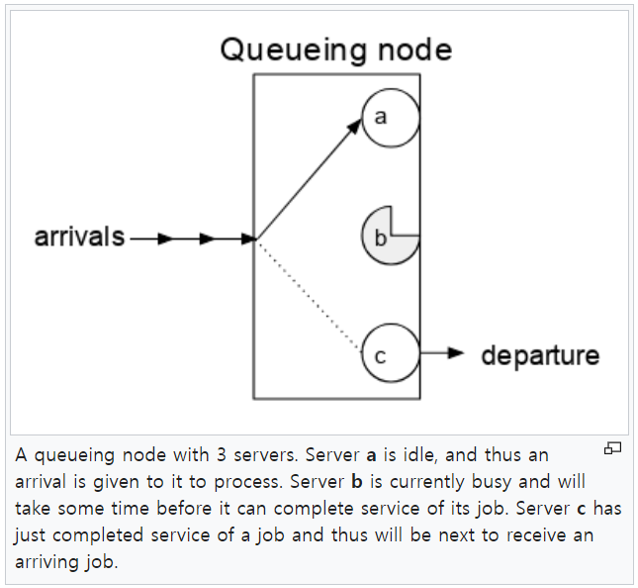
이 포스트에서 다루려고 하는 M/M/1 queue에서 M, M, 1은 각각 queue의 특성을 나타냅니다. 마지막의 1은 server의 개수를 의미합니다. 따라서 이 포스트에서는 server가 한 개인 간단한 경우에 대하여 다룹니다.

두 개의 M은 각각 arrival과 departure이 일어나는 방식을 나타냅니다. 여기서 M은 arrival(과 departure)이 일어나는 방식이 memoryless한 성질을 가진다는 것을 의미합니다. 즉, arrival들 사이의 시간간격의 확률분포가 memoryless 성질을 가진다는 것을 말합니다. 다시 말해, arrival이 일어나는 것과 departure가 일어나는 것이 모두 Poisson process라는 것을 가리키고 있는 것입니다.

arrival의 Poisson parameter가 $\lambda$이고 departure의 Poisson parameter가 $\mu$라고 하겠습니다. 이것은, arrival과 departure가 각각, 단위시간동안 평균적으로 $\lambda$회, $\mu$회 일어난다는 것을 의미합니다.

\[\begin{align*} \lambda &=\mathbb E\left[\text{# arrivals in unit time}\right]\\ \mu &=\mathbb E\left[\text{# departures in unit time}\right] \end{align*}\]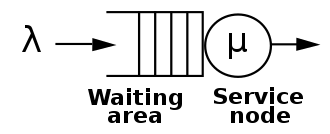

2.3 queue length $K_t$

queue의 상태는 실시간으로 변합니다. 예를 들어, 대기열의 길이(queue length)는 시간이 지남에 따라 바뀝니다. 시각 $t$에서의 대기열의 길이를 $K_t$라고 하면, 확률변수 $K_t$ 시간에 따른 추이를 생각해볼 수 있습니다.

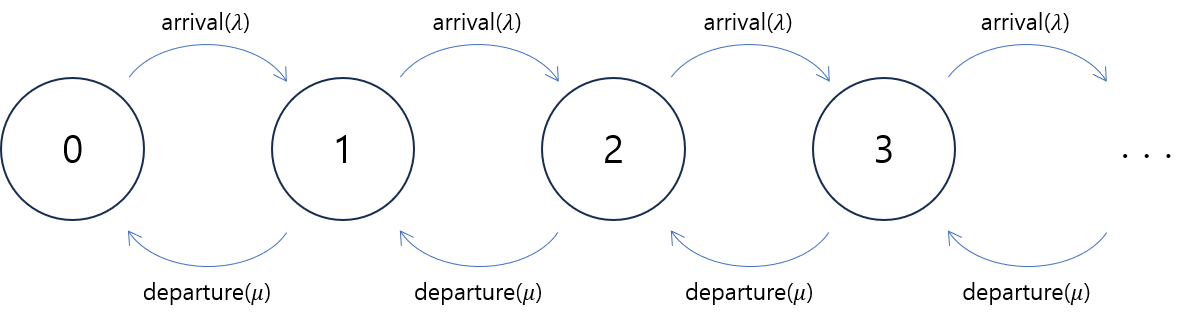
예를 들어, 시각 $t$에서의 대기열의 길이가 $2$였다고 할 때, 시각 $t+1$에서의 대기열의 길이는 $1$로 바뀔 수도 있고 $3$으로 바뀔 수도 있으며, $4$로 바뀔 수도 있습니다.

확률변수 $K_t$의 확률질량함수를 $p_k(t)$로 표시하면, 즉

\[p_k(t)=P\left(K_t=k\right)\tag{12}\]

라고 하면, 임의의 $t$에 대하여

\[p_0(t) + p_1(t) + p_2(t) + p_3(t) + \cdots = 1\tag{13}\]

이 성립합니다.

$p_k(t)$의 변화를 정확하게 분석하기 위해서 Poisson distribution 식을 유도했을 때처럼 시간을 잘게 쪼개는 방법을 사용할 수 있습니다. 단위시간동안 arrival은 $\lambda$번 발생하리라고 기대되므로, $\frac1m$ 만큼의 시간 동안에는 arrival이 $\frac\lambda m$번 발생하리라고 기대됩니다. 마찬가지로, $\frac1m$ 만큼의 시간동안 departure은 $\frac\mu m$번 발생하리라고 기대됩니다.

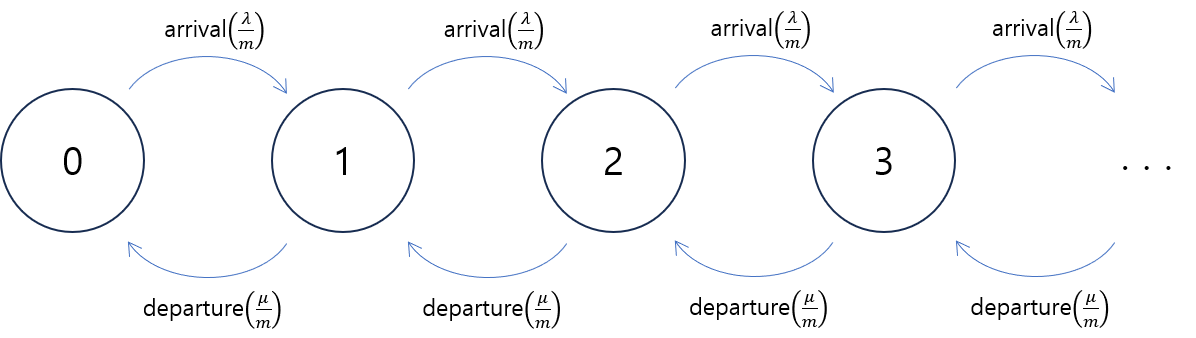
$m$이 충분히 크면, 구간 $\left[t, t+\frac1m\right]$동안 arrival 또는 departure이 두 번 이상 발생하지 않았다고 가정할 수 있습니다. 다시 말해, $\frac\lambda m$의 확률로 arrival이 발생하고, $\frac\mu m$의 확률로 departure이 발생합니다. 그러면, $p_n(t)$에 대한 점화식을 다음과 같이 얻을 수 있습니다 ;

\[\begin{align*} p_0\left(t+\tfrac1m\right)&=\left(1-\tfrac\lambda m\right)p_0(t)+\tfrac\mu mp_1(t)\\ p_1\left(t+\tfrac1m\right)&=\tfrac\lambda mp_0(t)+ \left(1-\tfrac\lambda m\right)\left(1-\tfrac\mu m\right)p_1(t)+\tfrac\mu mp_2(t)\\ p_2\left(t+\tfrac1m\right)&=\tfrac\lambda mp_1(t)+ \left(1-\tfrac\lambda m\right)\left(1-\tfrac\mu m\right)p_2(t)+\tfrac\mu mp_3(t)\\ &\vdots \end{align*}\]

다시 말해, $K_{t+\frac1m}=0$인 경우는 $K_t=0$이면서 arrival이 발생하지 않는 $\left(1-\tfrac\lambda m\right)$ 경우이거나 $K_t=1$이면서 departure가 발생하는 $\left(\tfrac\mu m\right)$ 경우로 나뉠 수 있습니다. 또한, $K_{t+\frac1m}=1$인 경우는 $K_t=0$이면서 arrival이 발생한 $\left(\tfrac\lambda m\right)$ 경우이거나 $K_t=1$이면서 arrival이나 departure가 모두 발생하지 않거나 $\left(1-\tfrac\lambda m\right)\left(1-\tfrac\mu m\right)$ 아니면 $K_t=2$이면서 departure가 발생한 경우$\left(\tfrac\mu m\right)$로 나뉠 수 있습니다.

조금 더 일반적으로 쓰면 다음과 같습니다. 즉, $K_{t+\frac1m}$의 확률질량함수는 $K_t$의 확률질량함수로 다음과 같이 표현할 수 있습니다.

\[\begin{align*} p_0\left(t+\tfrac1m\right) =&\left(1-\tfrac\lambda m\right)p_0(t)+\tfrac\mu mp_1(t) &&(k=0)\\ p_k\left(t+\tfrac1m\right) =&\tfrac\lambda mp_{k-1}(t)+\left(1-\tfrac\lambda m\right)\left(1-\tfrac\mu m\right)p_k(t)+\tfrac\mu mp_{k+1}(t) &&(k\ge1) \end{align*}\tag{14}\]

그러니까, $m$이 충분히 크면 $K_{t+\frac1m}=k$인 경우는 $K_t=k-1$, $K_t=k$, $K_t=k+1$인 경우에서만 발생할 수 있다고 가정하고 있는 것입니다.

식 (14)를 변형하면 $k=0$일 때,

\[\begin{align*} p_0\left(t+\tfrac1m\right) - p_0(t) &=-\frac\lambda m p_0(t) + \frac\mu mp_1(t)\\ \frac{p_k\left(t+\frac1m\right) - p_k(t)}{\frac1m} &=-\lambda p_k(t)+\mu p_{k+1}(t) \end{align*}\]

이고, 따라서 다음과 같은 미분방정식을 얻을 수 있습니다($m\to\infty$).

\[p_0'(t)=-\lambda p_0(t)+\mu p_1(t)\]

마찬가지로 $k=1,2,3,\cdots$일 때,

\[\begin{align*} p_k\left(t+\tfrac1m\right) - p_k(t) &=\frac\lambda mp_{k-1}(t)+\left(-\tfrac\lambda m-\tfrac\mu m+\tfrac{\lambda\mu}{m^2}\right)p_k(t)+\tfrac\mu mp_{k+1}(t)\\ \tfrac{p_k\left(t+\tfrac1m\right) - p_k(t)}{\tfrac 1m} &=\lambda p_{k-1}(t)+\left(-\lambda-\mu+\tfrac{\lambda\mu}m\right)p_k(t)+\mu p_{k+1}(t) \end{align*}\]

이고

\[p_k'(t)=\lambda p_{k-1}(t)+\left(-\lambda-\mu\right)p_k(t)+\mu p_{k+1}(t)\]

입니다. 정리하면 확률변수 $K_t$에 대한 확률질량함수 $p_k(t)$는 다음과 같은 연립미분방정식으로 표현될 수 있습니다 ;

\[\begin{align*} p_0'(t) &=-\lambda p_0(t)+\mu p_1(t) &&(k=0)\\ p_k'(t) &=\lambda p_{k-1}(t)+\left(-\lambda-\mu\right)p_k(t)+\mu p_{k+1}(t) &&(k\ge1) \end{align*}\tag{15}\]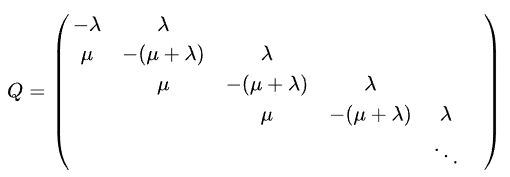

그런 의미에서 wikipedia에서는 M/M/1 queue model이 다음과 같은 rate transition matrix $Q$로 표현할 수 있다고 서술하고 있습니다.

2.4 stationary system

연립미분방정식 (15)를 통해 $p_k(t)$의 해를 analytic하게 구할 수 있습니다. 그 해는 조금 복잡하며, Bessel function을 포함하는 형태를 가집니다.

이 포스트에서 증명하려고 하는 식 (1)은 M/M/1 queue system이 평형상태 (stationary system)인 경우에서 성립하는 식입니다. 즉, $K_t$의 분포가 $t$에 따라서 변하지 않는 경우에 성립합니다. 그리고, $K_t$가 평형상태를 이루기 위한 필요충분조건은 $\lambda\le\mu$인 것으로 알려져 있습니다. 이에 대한 간략한 설명은 다음과 같습니다.

만약, $\lambda\gt\mu$이면, 즉, arrival이 departure보다 많으면, queue에 들어오는 client가 queue를 나가는 client보다 많다는 뜻이므로, queue에 계속해서 client가 쌓이는 경향성을 보이게 됩니다. 다시 말해, 시간 $t$ 따라 $K_t$가 점점 커지는 쪽으로 진행됩니다. 따라서 $\lambda\le\mu$이어야만 평형상태가 될 수 있습니다. 반대로, $\lambda\le\mu$이면 이 시스템은 평형상태를 이룹니다.

평형상태 조건인 $\lambda\le\mu$에서 조금 더 나아가 $\lambda\lt\mu$인 상황을 가정하겠습니다. 그러면, $t\to\infty$에서 $p_k’(t)=0$입니다. $p_k(t)$의 극한을

\[\pi_k = \lim_{t\to\infty}p_k(t)\]

라고 하면 $\pi_k$는 평형상태에서의 대기열의 길이

\[K=\lim_{t\to\infty}K_t\]

의 확률질량함수가 됩니다. 또한,

\[P(K=k)=\pi_k\]

입니다. 식 (15)에 $t\to\infty$를 적용하면

\[\begin{align*} 0&=-\lambda\pi_0+\mu\pi_1\\ 0&=\lambda\pi_{k-1}+\left(-\lambda-\mu\right)\pi_k+\mu\pi_{k+1} &&(k=1,2,3,\cdots) \end{align*}\]

입니다. 그러면

\[\begin{align*} \pi_1&=\frac\lambda\mu\pi_0\\ \pi_{k+1}-\pi_k&=\frac\lambda\mu(\pi_k-\pi_{k-1}) &&(k=1,2,3,\cdots) \end{align*}\]

이고 두번째 식을

\[\pi_{i+1}-\pi_i=\rho^i(\pi_1-\pi_0)\]

로 변형하면 $\left(\rho=\frac\lambda\mu\right)$

\(\begin{aligned} \pi_k &=\pi_0 + \sum_{i=0}^{k-1}(\pi_{i+1} - \pi_i)\\ &=\pi_0 + \frac{\left(\rho\pi_0-\pi_0\right)\left(1-\rho^k\right)}{1-\rho}\\ &=\pi_0 + \pi_0\left(\rho^k-1\right)\\ &=\pi_0\cdot\rho^k \end{aligned} \quad k=0,1,2,3\cdots \tag{16}\) 입니다.

즉, 수열 ${\pi_k}$는 $\pi_0$를 첫항으로 하고 공비가 $\rho$인 등비수열입니다. 그리고 $\pi_0$의 값도 결정될 수 있습니다. 왜냐하면, 식 (13)에서 $t\to\infty$를 하면

\[\pi_0+\pi_1+\pi_2+\cdots=1\]

이고 (16)을 적용하면

\[\frac{\pi_0}{1-\rho}=1\]

으로부터

\[\pi_0=1-\rho\]

이기 때문입니다. 따라서

\[\pi_k = (1-\rho)\rho^k\quad k=0,1,2,\cdots\tag{17}\]

입니다.

2.5 The expectation of $K$

이전 절에서 $K$는 평형상태에서의 대기열의 길이라고 했습니다. 이때, $K$는 확률변수였습니다. $\lambda\lt\mu$인 상태를 가정하고 있으므로 대기열이 점점 줄어드는 경향을 보이게 되겠지만, 그렇다고 하더라도 평형상태에서 $K$는 임의의 nonnegative 정수 값을 가질 수 있습니다. 그러니까, $K$는 $0$, $1$, $2$, $\cdots$의 값을 가질 가능성이 있습니다. 그리고 각각의 값 $k$를 가질 확률을 나타내는 확률질량함수가

\[P(K=k)=\pi_k=(1-\rho)\rho^k\]

임을 이전 절에서 유도했습니다.

그러면 이 블로그 포스트의 목적인 식 (1)을 증명할 준비가 다 되었습니다. 하지만 그 전에, 증명을 조금 더 쉽게 하기 위해, 다음과 같이 기본적인 계산을 먼저 해보겠습니다. 멱급수로 정의된 함수

\[f(x)=\sum_{k=0}^\infty x^k\]

를 생각하면 이 함수는 $\vert x\vert\lt1$인 조건에서

\[f(x)=\frac1{1-x}\]

이 성립합니다.

\[\sum_{k=0}^\infty x^k=\frac1{1-x}\]

의 양변을 $x$에 대해 미분하면

\[\sum_{k=1}^\infty kx^{k-1}=\frac1{(1-x)^2}\]

이 됩니다. $x=\rho$를 대입하면

\[\sum_{k=1}^\infty k\rho^{k-1}=\frac1{(1-\rho)^2}\tag{18}\]

입니다. 이제 $\mathbb E[K]$를 계산하면

\[\begin{align*} \mathbb E[K] &=\sum_{k=0}^\infty kP(K=k)\\ &\stackrel{(17)}=\sum_{k=0}^\infty k(1-\rho)\rho^k\\ &=\rho(1-\rho)\sum_{k=0}^\infty k\rho^{k-1}\\ &=\rho(1-\rho)\sum_{k=1}^\infty k\rho^{k-1}\\ &=\rho(1-\rho)\times\frac1{(1-\rho)^2}\\ &\stackrel{(18)}=\frac\rho{1-\rho} \end{align*}\]

입니다. 이로써 식 (1)이 증명되었습니다.

3. 마치며

지금까지 M/M/1 queue에서 대기열의 길이의 평균을 구하는 식을 유도해보았습니다. 여러 참고문헌들에 비해서는 꽤 많은 내용이 빠져있고, 유튜브 영상에 비해서는 자세히 적었습니다.

조금 더 글을 보완한다면 식 (15)에 대한 analytic한 해를 구해보고 관련된 Bessel function에 대한 내용을 적을 수 있을 것입니다. 또, stationary 조건에 대해 조금 더 엄밀하게 적을 필요가 있을 수도 있습니다. 그밖에, 확률론적인 개념들을 정확하게 서술할 필요도 있고 급수로 표현된 함수의 미분에 대해서도 이야기해야할 필요도 있습니다.

하지만, 당분간은 글의 내용을 더 추가하기보다는, 이미 쓴 내용들에서 잘못된 부분만 수정하는 정도로 그칠 것 같습니다.