10 분 소요

0. Overview

0.1. Motivation

0.2. 자료들

참고한 자료들은 다음의 세 개 입니다.

[1]에는 Lagrange multiplier에 대한 아주 기본적인 설명과 예제가 있습니다. [2]에는 Lagrange multiplier에 대한 증명 혹은 설명을 두 가지(기하학적인 설명, 해석적인 증명)로 제시하고 있습니다. 이때, [1]과 [2]는 모두 constraint의 개수가 1개인 Lagrange multiplier method에 대해 다루고 있고 변수의 개수는 각각 2개와 3개입니다. [3]에서는 constraint의 개수가 2개이고 변수의 개수가 3개인 Lagrange multiplier method의 방법론을 기하학적으로 증명하고, 예시도 들고 있습니다.

그러니까, 아주 일반적인 Lagrange multiplier에 대해서는 보지 않은 셈입니다. 다시 말해, 변수의 개수와 constraint의 개수가 임의로 주어지는 경우에 대해서는 공부하지 않았습니다. 이러한 일반적인 경우에 대해서는

에 자세히 설명되어 있는 듯합니다.

0.3. 이전 공부

학부 1학년 2학기에 Lagrange multiplier method에 대해 배웠습니다. 그런데 아마도 시험범위에는 속하지 않았던 것 같기도 합니다. 워낙 vector calculus에서 다루는 내용이 방대하니, Lagrange multiplier는 뒷전이었던 것 같습니다. 그 이후 해석학이나 다른 학부 수업에서는 이걸 다루는 걸 거의 못봤고, 기하학 수업에서 잠깐 K교수님이 언급하는 걸 들었던 것도 같습니다. 사실 1학년 수준에서 생각될 수 있는 기본적인 수학이라서 이후에 굳이 다룰 필요가 없었을는지도 모르겠습니다.

대학원에서, 매학기 초에 “미적분 조교자격시험”이라는 걸 치러야 했습니다. 이 시험은 한 번 통과하면 다음 학기에는 다시 치르지 않아도 됐는데, 제가 다닐 당시에는 이 시험을 너무 어렵게 내서 대학원생들 중 거의 아무도 시험에 통과하지 못했었습니다. 그러니까, 문제들 각각은 고민하면 풀리는 문제이긴 한데, 한시간 안에 풀려니 풀 수가 없었습니다. 그 때문에 거의 네 학기 정도 동안 (어느 순간엔가는 통과했습니다.) 매학기 초마다 1학년 미적분 전체 범위에 대해 시험을 봐야 했었고, 그때 Lagrange multiplier 문제가 꽤 자주 나왔었던 것 같습니다.

대학원에 다닐 동안 시험기간이면 늘 미적분 시험감독을 들어가야 했는데, 시험을 보는 1학년 학생들을 감독하는 게 조금 따분하거나 할 일이 없으면 시험지에 무슨 문제가 나왔나 들춰보기도 했습니다. 그리고, 문제 오류가 생기면 수정사항을 학생들에게 공지해주어야 하기 때문에도 시험문제들을 조금씩 보곤 했는데, 그때에도 Lagrange multiplier 문제가 보이곤 했습니다. 15년 전의 1학년 대상으로는 Lagrange multiplier 문제가 나오지 않았고 최근 학부에서는 시험문제로 나온 걸 보면, 그만큼 최근에는 최적화 기법을 포함한 응용수학이 강조되는 추세인 것 같기도 합니다.

0.4. 문제정의

Lagrange multiplier method는 다음과 같은 방법론을 지칭합니다. (조금 추상적으로 적어놓았습니다. 사전지식이 확실히 있는 것이 아니라면 다음 장으로 넘어갈 것을 권합니다.)

  1. 다음과 같은 최적화 문제가 있다고 합시다.

    Maximize $f(x_1,\cdots,x_n)$ subject to $\begin{cases}g_1(x_1,\cdots,x_n)&=k_1\\&\vdots\\g_m(x_1,\cdots,x_n)&=k_m\end{cases}$.

  2. 이 최적화문제를 풀기 위해서 다음과 같은 연립방정식을 풉니다.

    $$ \begin{cases} \nabla f(x_1,\cdots,x_n) + \lambda_1\nabla g_1(x_1,\cdots,x_n)+\cdots+\lambda_m\nabla g_m(x_1,\cdots,x_n)=0\\ g_j(x_1,\cdots,x_n)=k_j\quad(j=1,2,\cdots,m) \end{cases} $$

  3. 연립방정식의 해가 $(x_1,\cdots,x_n)=\left({x_1}^{(1)},\cdots,{x_n}^{(1)}\right), \cdots, \left({x_1}^{(L)},\cdots,{x_n}^{(L)}\right)$ 과 같이 $L$개 주어진다면, 이 중에서 위 최적화문제의 답이 있습니다. 그러니까, $f\left({x_1}^{(1)},\cdots,{x_n}^{(1)}\right)$, $\cdots$, $f\left({x_1}^{(L)},\cdots,{x_n}^{(L)}\right)$ 를 각각 계산하고 이 중에 가장 큰 값을 고르면 그 값이 구하고자 하는 최댓값이 됩니다.

이와 관련한 몇가지 사항들입니다.

  • 1에서 $f$를 objective function(목적함수)라고 하고, $g_j(x_1,\cdots,x_n)=k_j$ 꼴의 식들을 constraint(제약조건)라고 합니다. 여기에서 $f$는 $f:\mathbb R^n\to\mathbb R$이고, $g_j$도 $g_j:\mathbb R^n\to\mathbb R$입니다. 즉, $f$와 $g_j$는 모두 다변수 실함수입니다.
  • 일반성을 잃지 않고 $k_j$들을 모두 $0$으로 두어도 괜찮습니다. 그러니까, $g_j(x_1,\cdots,x_n)=k_j$라는 제약조건이 있었다면, 새로운 함수 $g’_j$를 $g’_j(x_1,\cdots,x_n)=g_j(x_1,\cdots,x_n)-k_j$으로 둘 수 있습니다. 그러면 제약조건이 $g’_j(x_1,\cdots,x_n)=0$의 형태로 바뀔 수 있다는 것입니다.
  • 2에서 $f$와 $g_j$의 gradient가 있으므로 $f$와 $g_j$는 당연히 미분가능한 함수여야 합니다. 적어도 모든 종류의 partial derivative(편미분계수)들이 존재해야 합니다.

  • 2는 “잘 풀리는” 연립방정식입니다. 다시 말해, 변수의 개수와 식의 개수가 같습니다. 변수는 $x_1$, $\cdots$, $x_n$, $\lambda_1$, $\cdots$, $\lambda_m$의 $n+m$개이고, 식도

    \[\begin{align*} \frac{\partial f}{\partial x_1}(x_1,\cdots,x_n)=&\lambda_1\frac{\partial g_1}{\partial x_1}(x_1,\cdots,x_n)+\cdots+\lambda_m\frac{\partial g_m}{\partial x_1}(x_1,\cdots,x_n)\\ &\vdots\\ \frac{\partial f}{\partial x_n}(x_1,\cdots,x_n)=&\lambda_1\frac{\partial g_1}{\partial x_n}(x_1,\cdots,x_n)+\cdots+\lambda_m\frac{\partial g_m}{\partial x_n}(x_1,\cdots,x_n)\\ g_1(x_1,\cdots,x_n) =& k_1\\ &\vdots\\ g_m(x_1,\cdots,x_n) =& k_m\\ \end{align*}\]

    의 $n+m$개이기 때문입니다.

  • 2에서 첫번째 식 대신에, $\nabla g_i$들을 모두 우변으로 이항한

    \[\nabla f(x_1,\cdots,x_n) = \lambda_1\nabla g_1(x_1,\cdots,x_n)+\cdots+\lambda_m\nabla g_m(x_1,\cdots,x_n)\tag{$\star$}\]

    으로 바꿔도 당연히 문제를 푸는 데는 지장이 없습니다. 이 포스트에서는 $k=1$일 때 $(\star)$ 식을 사용하고 $k=2$일 때는 원래 식을 사용합니다.

  • 최댓값을 구하는 것만 썼지만, 최솟값을 구하는 것도 똑같은 방식으로 진행될 수 있습니다. 그러니까 Lagrange multiplier method는 일반적으로 주어진 실함수의 optima(최댓값과 최솟값)를 구하는 방법입니다.
  • 위 식에서의 $\lambda_j$를 Lagrange multiplier라고 부릅니다. 그러니까, 이러한 최적화 기법을 보통 Lagrange multiplier 라고 부르긴 하지만 더 정확하게는 Lagrange multiplier method(라그랑지 승수법) 라고 불리는 게 맞을 것 같습니다.

문제의 formulation을 꽤 일반적으로 적어보았습니다. 그래서 잘 눈에 들어오지 않을 수 있는데, 이후부터는 더 쉽게 서술할 것 같습니다. 다만, 지금 여기에 쓴 것보다도 더 일반적으로 많이 기술되는 경우가 많은 것 같습니다. 예를 들어, $g_1$, $\cdots$, $g_m$을 합쳐서 하나의 $g:\mathbb R^n\to\mathbb R^m$으로 쓸 수 있을 것이고, 그러면 $\lambda$도 하나의 벡터 $\boldsymbol \lambda=\begin{bmatrix}\lambda_1\cdots\lambda_n\end{bmatrix}^T$로서 표현할 수도 있을 것이며, $(x_1,\cdots x_n)$과 같은 표현도 $\boldsymbol x=\begin{bmatrix}x_1\cdots x_n\end{bmatrix}^T$로 나타낼 수 있을 것입니다.

그런 식으로 서술되어 있는 곳이 위키피디아입니다. Summary and rationale은 굉장히 추상적으로 쓰여져있고, Statement도 마찬가지로 쉽지 않게 쓰여져있습니다.

Lagrange multiplier의 방법론이 성립한다는 사실을 “if (…) then (…)” 형식의 조건문으로 서술하면 다음과 같이 될 것입니다.

정리
제약조건 $g_1(x_1,\cdots,x_n)=k_1$, $\cdots$, $g_m(x_1,\cdots,x_n)=k_m$ 하에서 $f$가 $P^\ast$에서 최댓값(최솟값)을 가지면 $\nabla f(P^\ast)+\lambda_1\nabla g_1(P^\ast)+\cdots+\lambda_m\nabla g_m(P^\ast)=0$를 만족시키는 실수 $\lambda_1$, $\cdots$, $\lambda_m$이 존재한다.

1. A Simple Example

여기에서는 아주 간단한 Lagrange multiplier의 예시를 들고 있습니다.

1.1. 문제

  1. 다음과 같은 최적화 문제가 있다고 합시다.

    제약조건 $g(x,y)=k$ 하에서 $f(x,y)$의 최댓값을 구하여라.

  2. 이 최적화문제를 풀기 위해서 다음과 같은 연립방정식을 풉니다.

    $$ \begin{cases} \nabla f(x,y)=\lambda\nabla g(x,y)\\ g(x,y)=k \end{cases} $$

  3. 연립방정식의 해가 $(x,y)=(x^{(1)},y^{(1)}), \cdots, (x^{(L)},y^{(L)})$ 과 같이 $L$개 주어진다면, 이 중에서 위 최적화문제의 답이 있습니다. 그러니까, $f(x^{(1)},y^{(1)}), \cdots, f(x^{(L)},y^{(L)})$ 를 각각 계산하고 이 중에 가장 큰 값을 고르면 그 값이 구하고자 하는 최댓값이 됩니다.

만약 $f$와 $g$가

\[\begin{align*} f(x,y)&=8x^2-2y\\ g(x,y)&=x^2+y^2 \end{align*}\]

이고 $k=1$이면, 다음과 같은 문제가 됩니다.

제약조건 $x^2+y^2=1$ 하에서 $8x^2-2y$의 최댓값을 구하여라.

1.2. 풀이(이차함수)

이 문제는 너무 간단한 문제여서 굳이 Lagrange multiplier를 쓰지 않아도 됩니다. 예를 들어 중학교 3학년에서 배우는 ‘이차함수’를 사용하면

\[\begin{align*} 8x^2-2y &=8(1-y^2)-2y\\ &=-8y^2-2y+8\\ &=-8\left(y+\frac18\right)^2+\frac{65}8 \end{align*}\]

이 됩니다. 즉 $8x^2-2y$는 $(x,y)=\left(\pm\frac{3\sqrt7}8,-\frac18\right)$에서 최댓값 $\frac{65}8$을 가집니다.

1.3. 풀이(부등식의 영역)

고등학교 1학년 수준의 ‘부등식의 영역’으로도 풀릴 수 있습니다. 사실 2015년 개정 교육과정으로 오면서 이것이 고등학교 1학년 범위에서 빠졌지만, 그래도 진로선택과목으로서 ‘경제 수학’에 해당 내용이 있는 것 같으니, 어쨌든 고등학교 수학에 속하는 수준으로 풀립니다. 다음과 같이 풀면 됩니다.

$8x^2-2y$를 $m$으로 둡니다. 즉,

\[8x^2-2y=m\]

로 둡니다. 그러면 문제는

$x^2+y^2=1$, $8x^2-2y=m$를 만족하는 $m$의 최댓값을 구하여라.

로 바뀔 수 있습니다. 이것을 조금 더 정확하게 쓰면

두 식 $x^2+y^2=1$, $8x^2-2y=m$를 모두 만족시키는 $(x,y)$가 존재할 때, $m$의 최댓값을 구하여라.

라고 바꿔쓸 수 있습니다. 이것은 또다시,

두 그래프 $x^2+y^2=1$, $8x^2-2y=m$의 교점이 존재할 때, $m$의 최댓값을 구하여라.

로 바뀔 수 있습니다. 좀 더 엄밀하게 쓰면

두 그래프 $\{(x,y):x^2+y^2=1\}$, $\{(x,y):8x^2-2y=m\}$의 교점이 존재할 때, $m$의 최댓값을 구하여라.

와 같이 쓰일 수도 있을겁니다. 여하튼, 그러면 문제는 너무 쉬워집니다.

첫번째 그래프인 단위원은 고정되어 있고, 두번째 그래프인 포물선은 $m$값에 따라 달라집니다. 정확하게는,

\[\begin{gather*} 8x^2-2y=m\\ y=4x^2-\frac m2 \end{gather*}\]

로부터 포물선의 개형($4$)은 일정한데 꼭짓점 $(0,-\frac m2)$의 $y$좌표가 바뀝니다.

$m$의 값을 변경해가면서 두 그래프가 교차하는 경우를 따져보면 아래 그림과 같습니다.

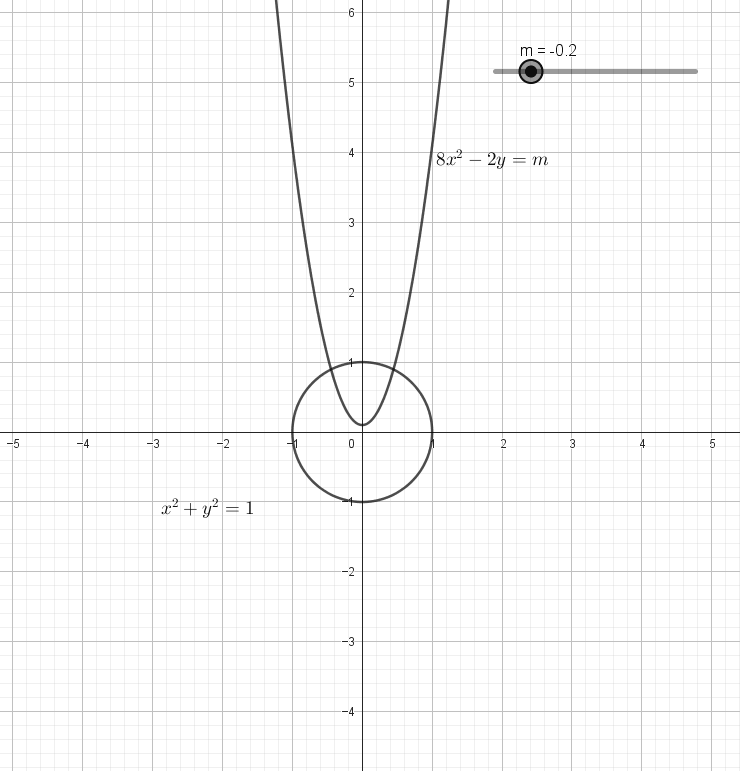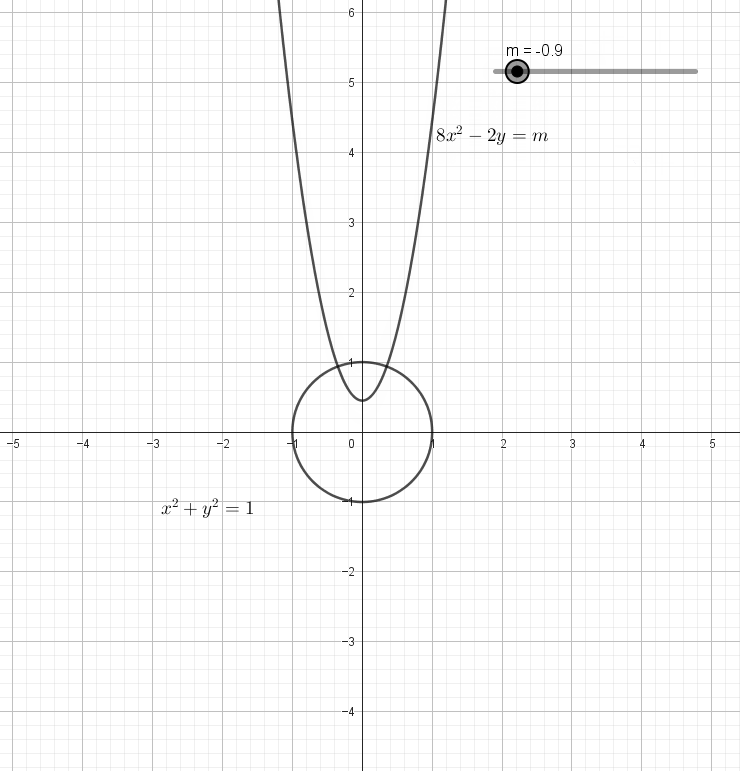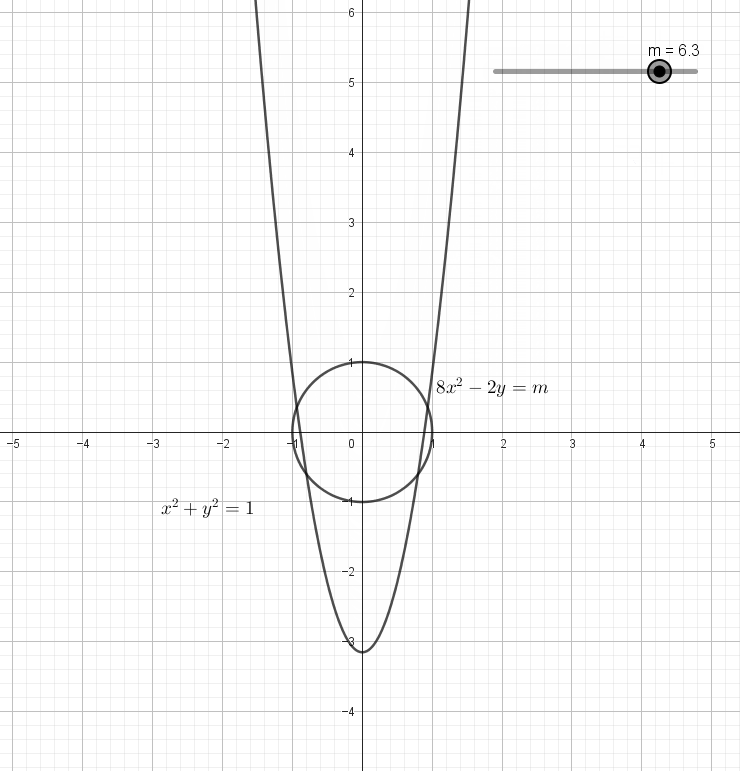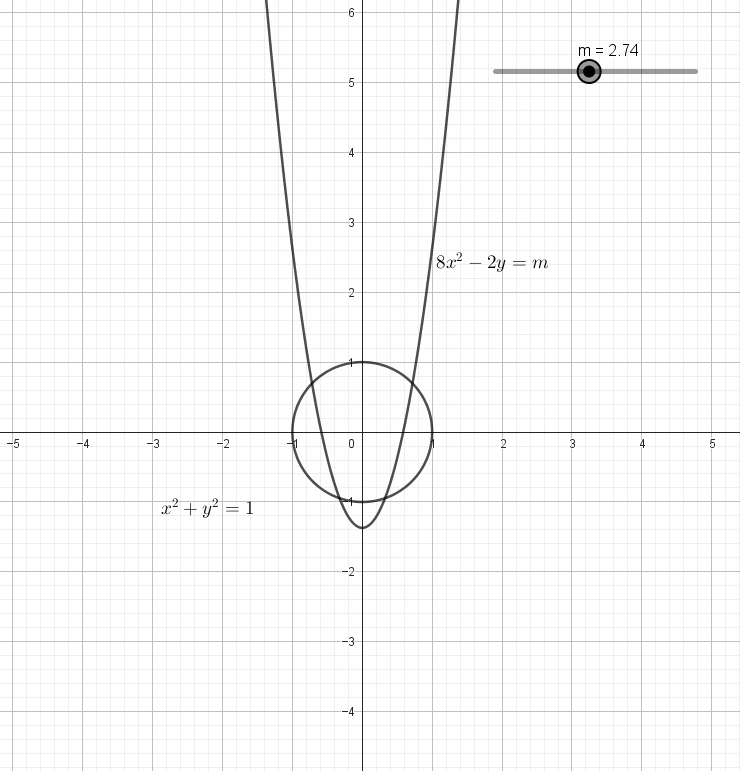
$m$의 값이 가장 클 때에는 꼭짓점의 $y$좌표가 가장 작을 때이므로 포물선과 원이 아래에서 접할 때입니다.

이 경우의 $m$값을 구하기 위해서 (판별식을 쓰면 답을 쉽게 구할 수 있지만, 좀 더 정확하게 구하기 위해) 미분을 활용할 수 있습니다. 두 식

\[\begin{align*} 8x^2-2y&=m\\ x^2+y^2&=1 \end{align*}\]

의 양변을 $x$에 대해 미분하면

\[\begin{align*} 16x-2\frac{dy}{dx}&=0\\ 2x+2y\frac{dy}{dx}&=0 \end{align*}\] \[\begin{align*} 8x-\frac{dy}{dx}&=0\\ x+y\frac{dy}{dx}&=0 \end{align*}\]

에서

\[x+8xy=0\]

이고

\[x(1+8y)=0\]

입니다.

그러면 $x=0$ 이거나 $y=-\frac18$입니다. 그런데 $\frac{dy}{dx}=8x$가 양수 또는 음수인 경우를 찾고 있으므로 $x\ne0$이고 따라서 $y=-\frac18$입니다. 이때의 $x$는 $x=\pm\frac{3\sqrt7}8$이고, 따라서 $(x,y)=\left(\pm\frac{3\sqrt7}8,-\frac18\right)$ 이며, 구하는 최댓값은 $m=8x^2-2y=\frac{65}8$이 됩니다.

참고로 판별식을 사용한 풀이는 다음과 같습니다.

\[\begin{gather*} 8x^2-2y=m\\ 8(1-y^2)-2y=m\\ -8y^2-2y+8-m=0\\ \frac D4=1+8(8-m)=0\\ m=\frac{65}8 \end{gather*}\]

1.4. 풀이(Lagrange multiplier)

이번에는 Lagrange multiplier로 이 문제를 풀어보겠습니다.

  1. 풀어야 하는 최적화 문제는

    제약조건 $g(x,y)=k$ 하에서 $f(x,y)$의 최댓값을 구하여라.

    이고 이때, $f(x,y)=8x^2-2y$, $g(x,y)=x^2+y^2$, $k=1$입니다.

  2. 이 문제를 풀기 위한 연립방정식은

    $$ \begin{cases} \nabla f(x,y)=\lambda\nabla g(x,y)\\ g(x,y)=k \end{cases} $$

    이고, 이것을 다시 풀면

    \[\begin{align*} f_x(x,y)&=\lambda g_x(x,y)\\ f_y(x,y)&=\lambda g_y(x,y)\\ g(x,y)&=k \end{align*}\]

    입니다. 이때, $f_x=\frac{\partial f}{\partial x}$, $f_y=\frac{\partial f}{\partial y}$, $g_x=\frac{\partial g}{\partial x}$, $g_y=\frac{\partial g}{\partial y}$입니다. 따라서 지금 풀어야 하는 연립방정식은

    \[\begin{align*} 16x&=2\lambda x\tag1\\ -2&=2\lambda y\tag2\\ x^2+y^2&=1\tag3 \end{align*}\]

    입니다. (변수 3개, 식 3개) (1)에서 $x=0$이거나 $\lambda=8$입니다.

    만약 $x=0$이면, (3)으로부터 $y=\pm 1$이고 (2)로부터 이때의 $\lambda$는 $\lambda=\mp1$이 됩니다.

    만약 $\lambda=8$이면, (2)에서 $y=-\frac18$이고 (3)으로부터 $x=\pm\frac{3\sqrt7}8$입니다.

  3. 따라서 연립방정식의 해는 $(x,y)=(0,1), (0,-1), \left(\frac{3\sqrt7}8,-\frac18\right), \left(-\frac{3\sqrt7}8,-\frac18\right)$ 이 됩니다. 각각의 경우에 대하여 $f(x,y)$를 계산하면

    \[\begin{align*} f(0,1)&=-2\\ f(0,-1)&=2\\ f\left(\frac{3\sqrt7}8,-\frac18\right)&=\frac{65}8\\ f\left(-\frac{3\sqrt7}8,-\frac18\right)&=\frac{65}8 \end{align*}\]

    입니다. 따라서 $f(x,y)$의 최댓값은 $\frac{65}8$이고 최대일 때의 $x$와 $y$는 $(x,y)=\left(\pm\frac{3\sqrt7}8,-\frac18\right)$ 입니다. 이것은 이차함수나 부등식의 영역을 통해 구한 답과 일치합니다.

1.5. 해석(Lagrange multiplier)

이러한 Lagrange multiplier 방식의 풀이가 왜 유효한지에 대한 설명은 다음과 같습니다.

1.3에서 이 최적화 문제는

두 그래프 $\{(x,y):g(x,y)=k\}$, $\{(x,y):f(x,y)=m\}$의 교점이 존재할 때, $m$의 최댓값을 구하여라.

와 같이 쓰일 수 있다고 했습니다. (단, $f(x,y)=8x^2-2y$, $g(x,y)=x^2+y^2$, $k=1$.)

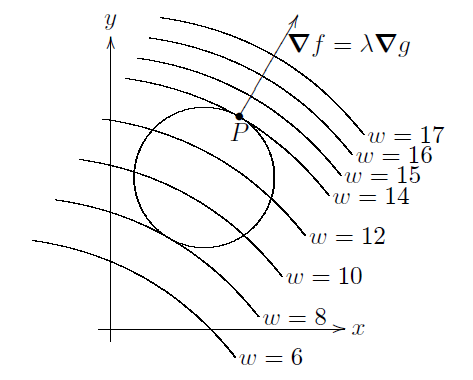
그러면 $m$값이 최대 또는 최소가 되는 순간은 두번째 도형(포물선)이 $m$값에 따라 움직이다가, 첫번째 도형(단위원)에서 막 떨어지는, 닿을락 말락한 순간입니다. 그리고 그 순간은 $f$와 $g$의 gradient가 서로 같은 방향을 가리키는 (혹은 반대방향을 가리키는) 순간입니다. 즉,

\[\nabla f\parallel\nabla g\]

이어야 합니다. 따라서, $f(x,y)$가 최댓값을 가지는 때는 $\nabla f(x,y)=\lambda\nabla g(x,y)$을 만족시키는 실수 $\lambda(\ne0)$가 존재하는 때인 것입니다. 아래 그림은 [2]에 나오는 그림이지만 왜 $f$가 최댓값을 가질 때 $\nabla f\parallel\nabla g$여아 하는지를 잘 설명해주는 그림이니 여기에 첨부합니다.

2. One multiplier

MIT의 자료 [2]에서는 아주 우아하고 깔끔하게, Lagrange multiplier에 대한 문제 정의와 기하학적인 설명, 그리고 해석적인 증명을 보여주고 있습니다. 꼭 필요한 말들만 적어서 간결하게 설명하고 있습니다. 여기에서는 문제 정의와 해석적인 증명만 옮겨보았습니다.

2.1. 문제 정의

  1. 변수가 3개인 함수 $f$에 대한 최적화문제

    제약조건 $g(x,y,z)=k$ 하에서 $f(x,y,z)$의 최댓값을 구하여라.

    를 풀기위해서는

  2. 연립방정식

    $$ \begin{cases} \nabla f(x,y,z)=\lambda\nabla g(x,y,z)\\ g(x,y.z)=k \end{cases} $$

    를 풀고,

  3. 그 연립방정식의 해들을 대입하여 $f(x,y,z)$가 가장 큰 경우를 구하면 $f$의 최댓값을 구하는 것이 됩니다.

그리고, 이것은 다음과 같은 정리로 서술될 수 있습니다.

정리
제약조건 $g(x,y,z)=k$ 하에서 $f(x,y,z)$가 $P^\ast(x^\ast,y^\ast,z^\ast)$에서 최댓값을 가지면 $\nabla f(x^\ast,y^\ast,z^\ast)=\lambda\nabla g(x^\ast,y^\ast,z^\ast)$를 만족시키는 실수 $\lambda$가 존재합니다.

MIT 자료에서는 이 정리를 기본적인 vector calculus를 사용하여 증명합니다.

2.2. 증명

$g$가 미분가능한 것을 가정하고 있으므로 제약조건 $g(x,y,z)=k$은 하나의 곡면 $\alpha$를 의미합니다. 주어진 최적화문제는, 점 $P(x,y,z)$가 곡면 $\alpha$ 위에서 움직일 때, $f(x,y,z)$의 최댓값을 구하는 문제가 됩니다.

위 정리의 가정에 의하면, $f$는 이 곡면 $\alpha$ 위의 점 $P^\ast(x^\ast,y^\ast,z^\ast)$에서 최댓값을 가집니다. 곡선 $\boldsymbol r(t)=\left(x(t), y(t), z(t)\right)$을 $\boldsymbol r(0)=P^\ast$를 만족시키는 곡면 $\alpha$ 위의 임의의 곡선이라고 가정하면, 곡선 $\boldsymbol r:\mathbb R\to\mathbb R^3$와 $f:\mathbb R^3\to\mathbb R$의 합성함수인 $f\circ \boldsymbol r:\mathbb R\to\mathbb R$은 $t=0$에서 최댓값을 가지는 실함수입니다. 즉, 함수

\[t\mapsto f\left(x(t),y(t),g(t)\right)\]

는 $t=0$에서 최댓값을 가지는 함수입니다. 따라서,

\[\frac{d}{dt}\left[f\left(x(t),y(t),z(t)\right)\right]=0\]

입니다. 그러면 연쇄법칙(chian rule)에 의해

\[\left.\frac{dx}{dt}\frac{\partial f}{\partial x}+\frac{dy}{dt}\frac{\partial f}{\partial y}+\frac{dz}{dt}\frac{\partial f}{\partial z}\right|_{t=0}=0\]

입니다. 이것을 다시 쓰면

\[\left.\left(\frac{dx}{dt},\frac{dy}{dt},\frac{dz}{dt}\right) \cdot \left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}\right)\right|_{t=0}=0\]

이고, 따라서

\[\boldsymbol r'(0) \cdot \nabla f(x^\ast,y^\ast,z^\ast) =0\]

입니다.

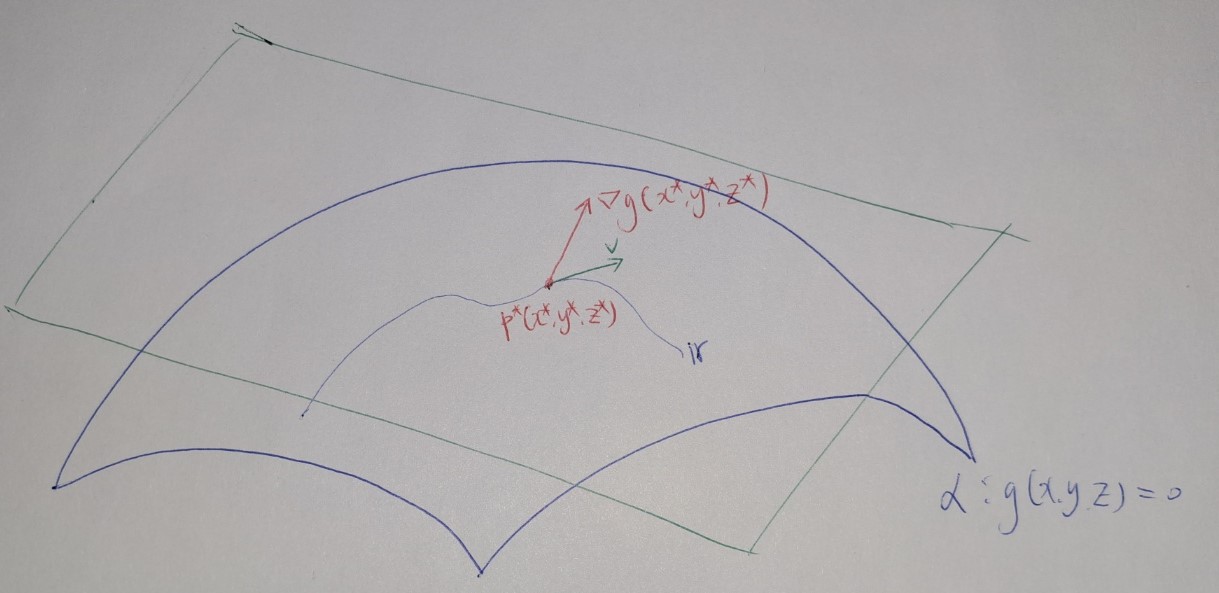
그런데 $\boldsymbol r$이 $\boldsymbol r(0)=P^\ast$를 만족시키는 곡면 $\alpha$ 위의 임의의 곡선이었으므로, 곡면 $\alpha$의 $P^\ast$에서의 접평면 위의 임의의 벡터 $v$에 대하여

\[v\cdot \nabla f(x^\ast,y^\ast,z^\ast)=0\]

입니다. 그렇다는건, $\nabla f(x^\ast,y^\ast,z^\ast)$이 $\alpha$의 $P^\ast$에서의 법선벡터라는 말입니다. 이때, $\nabla g(x^\ast, y^\ast, z^\ast)$도 마찬가지로 $\alpha$의 $P^\ast$에서의 법선벡터이므로, 두 벡터 $\nabla g(x^\ast, y^\ast, z^\ast)$와 $\nabla f(x^\ast,y^\ast,z^\ast)$는 서로 평행하거나 반대방향일 수밖에 없습니다. 그러므로

\[\nabla g(x^\ast, y^\ast, z^\ast)=\lambda\nabla f(x^\ast,y^\ast,z^\ast)\]

를 만족시키는 실수 $\lambda$가 존재합니다. $\square$

3. Two multipliers

이 자료에서는 제약조건이 두 개인 경우에 대해 설명합니다. 따라서 Lagrange multiplier도 $\lambda_1$, $\lambda_2$의 두 개인 경우를 다루고 있습니다.

이 부분은 따로 pdf 파일을 만들어두기도 했습니다. [3]과 pdf 파일에서는 최솟값을 구하는 경우를 다루고 있는데 여기에서는 이전 장과의 연관성을 고려해 최댓값을 구하는 문제를 고려했습니다. 그래서 pdf 파일과 이 포스트는 증명 과정의 부등호에 있어 약간의 차이가 있습니다.

3.1. 문제 정의

  1. 변수가 3개이고 제약조건이 2개인 함수 $f$에 대한 최적화문제

    제약조건 $g_1(x,y,z)=k_1$, $g_2(x,y,z)=k_2$ 하에서 $f(x,y,z)$의 최댓값을 구하여라.

    를 풀기위해서는

  2. 연립방정식

    $$ \begin{cases} \nabla f(x,y,z)+\lambda_1\nabla g_1(x,y,z)+\lambda_2\nabla g_2(x,y,z)=0\\ g_1(x,y,z)=k_1\\ g_2(x,y,z)=k_2\\ \end{cases} $$

    를 풀고,

  3. 그 연립방정식의 해들을 대입하여 $f(x,y,z)$가 가장 큰 경우를 구하면 $f$의 최댓값을 구하는 것이 됩니다.

위의 연립방정식을 상세하게 풀면

\[\begin{gather*} \frac{\partial f}{\partial x}(x,y,z)+\lambda_1\frac{\partial g_1}{\partial x}(x,y,z)+\lambda_2\frac{\partial g_2}{\partial x}(x,y,z)=0\\ \frac{\partial f}{\partial y}(x,y,z)+\lambda_1\frac{\partial g_1}{\partial y}(x,y,z)+\lambda_2\frac{\partial g_2}{\partial y}(x,y,z)=0\\ \frac{\partial f}{\partial z}(x,y,z)+\lambda_1\frac{\partial g_1}{\partial z}(x,y,z)+\lambda_2\frac{\partial g_2}{\partial z}(x,y,z)=0\\ g_1(x,y,z)=k_1\\ g_2(x,y,z)=k_2 \end{gather*}\]

입니다. 그리고, 이것은 다음과 같은 정리로 서술될 수 있습니다.

정리
제약조건 $g_1(x,y,z)=k_1$, $g_2(x,y,z)=k_2$ 하에서 $f(x,y,z)$가 $P^\ast(x^\ast,y^\ast,z^\ast)$에서 최댓값을 가지면 $\nabla f(x^\ast,y^\ast,z^\ast)+\lambda_1\nabla g_1(x^\ast,y^\ast,z^\ast)+\lambda_2\nabla g_2(x^\ast,y^\ast,z^\ast)=0$를 만족시키는 실수 $\lambda_1$, $\lambda_2$가 존재한다.

3.2. 증명

$g_1$, $g_2$가 미분가능하다는 것을 가정하고 있으므로 제약조건 $g_1(x,y,z)=k_1$, $g_2(x,y,z)=k_2$는 각각 곡면 $\alpha_1$, $\alpha_2$을 의미합니다. 두 곡면 $\alpha_1$과 $\alpha_2$가 $P^\ast(x^\ast,y^\ast,z^\ast)$의 근방에서 서로 일치하지 않는다고 가정하면, $\alpha_1$과 $\alpha_2$는 교선 $l:g_1-k_1=g_2-k_2=0$을 형성합니다. (아래 그림에서, $\alpha_1$은 검은 곡면, $\alpha_2$는 파란 곡면, $l$은 빨간 곡선) 그렇다면 주어진 최적화문제는, 점 $P(x,y,z)$가 교선 $l$ 위에서 움직일 때, $f(x,y,z)$의 최댓값을 구하는 문제가 됩니다.

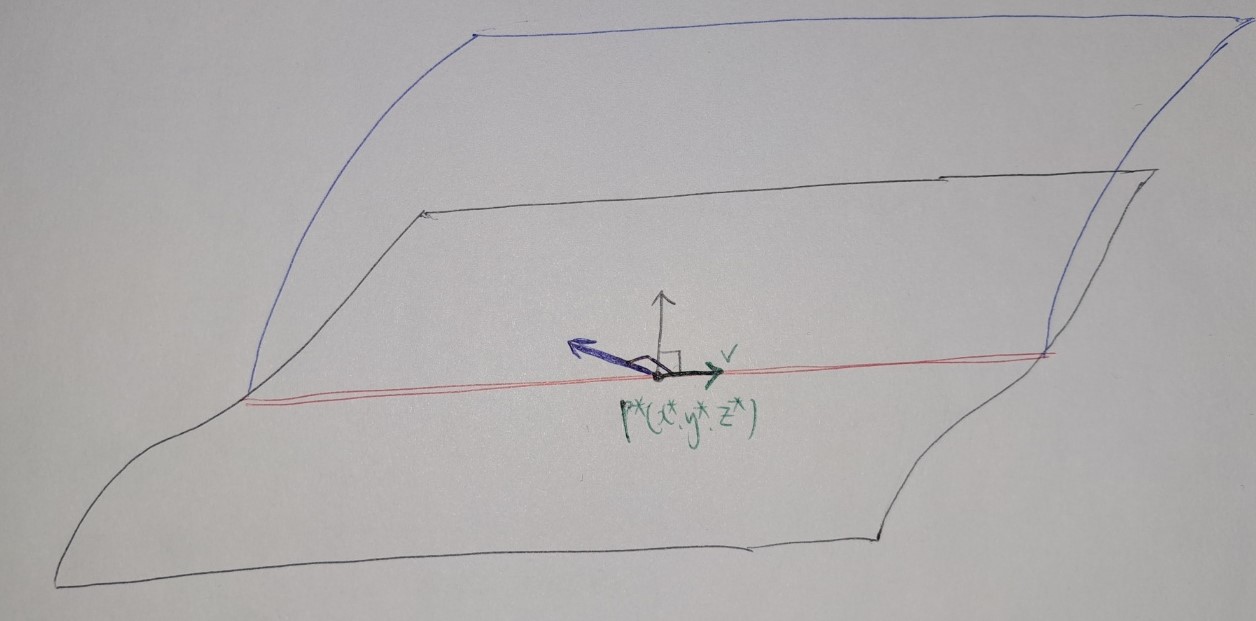
위 정리의 가정에 의하면 $f$는 이 교선 $l$ 위의 점 $P^\ast(x^\ast,y^\ast,z^\ast)$에서 최댓값을 가집니다. 이때, 교선 $l$은 미분가능한 곡선이므로, 점 $P^\ast$를 지나는 $l$의 한 접선방향 $v$를 생각할 수 있습니다. (단, $v$는 단위벡터, $||v||=1$.) $f$가 $P^\ast$에서 최댓값을 가지므로, $f$의 $v$방향의 방향도함수(directional derivative)는 0보다 작거나 같습니다. 즉,

\[D_vf(x^\ast,y^\ast,z^\ast)\le0\]

이고, 따라서

\[\nabla f(x^\ast,y^\ast,z^\ast)\cdot v\le0\tag{$*$}\]

입니다. 그런데, $f$의 $-v$방향의 방향도함수 또한 0보다 작거나 같습니다. 그러니까

\[D_{-v}f(x^\ast,y^\ast,z^\ast)\le0\]

이고,

\[\nabla f(x^\ast,y^\ast,z^\ast)\cdot v\le0\tag{$**$}\]

입니다. 그러면 $(*)$와 $(**)$으로부터

\[\nabla f(x^\ast,y^\ast,z^\ast)\cdot v=0\tag4\]

입니다. (이상의 과정은 2.2에서 했던 것처럼 $\boldsymbol r(0)=v$인 $\boldsymbol r:\mathbb R\to\mathbb R^3$을 도입해서 설명해도 마찬가지로 설명될 수 있을 겁니다.)

한편, 벡터 $v$는 곡면 $\alpha_1$에 속하므로 $v$는 곡면 $\alpha_1$에서의 법선벡터인 $\nabla g_1(x^\ast, y^\ast, z^\ast)$에 직교합니다. 즉, \(\nabla g_1(x^\ast,y^\ast,z^\ast)\cdot v = 0\tag5\) 입니다. 마찬가지로 \(\nabla g_2(x^\ast,y^\ast,z^\ast)\cdot v = 0\tag6\) 입니다.

$\mathbb R^3$에서의 $v$의 orthogonal complement를 $v^\perp$이라고 쓰면, $v^\perp$는 원점을 지나고 $v$를 법선벡터로 가지는 평면이므로 2차원의 벡터공간입니다. 그러면 (4), (5), (6)으로부터 각각

\[\begin{align*} \nabla f(x^\ast,y^\ast,z^\ast)&\in v^\perp\\ \nabla g_1(x^\ast,y^\ast,z^\ast)&\in v^\perp\\ \nabla g_2(x^\ast,y^\ast,z^\ast)&\in v^\perp \end{align*}\]

입니다.

그리고, 두 곡면 $\alpha_1$과 $\alpha_2$가 $P^\ast$의 근방에서 서로 일치하지 않는다고 가정하고 있으므로

\[\nabla g_1(x^\ast,y^\ast,z^\ast)\not\parallel\nabla g_2(x^\ast,y^\ast,z^\ast)\]

입니다. 따라서, $\nabla g_1(x^\ast,y^\ast,z^\ast)$, $\nabla g_2(x^\ast,y^\ast,z^\ast)$는 $v^\perp$의 기저(basis)를 이룹니다. 그러므로 $\nabla f(x^\ast,y^\ast,z^\ast)$는 $\nabla g_1(x^\ast,y^\ast,z^\ast)$와 $\nabla g_2(x^\ast,y^\ast,z^\ast)$의 일차결합으로 표현될 수 있습니다. 즉,

\[\nabla f(x^\ast,y^\ast,z^\ast)=(-\lambda_1)\nabla g_1(x^\ast,y^\ast,z^\ast)+(-\lambda_2)\nabla g_2(x^\ast,y^\ast,z^\ast)\]

를 만족시키는 실수 $\lambda_1$, $\lambda_2$가 존재합니다.

따라서,

\[\nabla f(x^\ast,y^\ast,z^\ast)+\lambda_1\nabla g_1(x^\ast,y^\ast,z^\ast)+\lambda_2\nabla g_2(x^\ast,y^\ast,z^\ast)=0\]

이 성립합니다. $\square$

4. 마치며

지금까지 Lagrange multiplier method에 대해 써봤습니다. 처음 생각했던 것보다는 훨씬 시간이 많이 들기는 했는데, 그래도 마쳤다는 것에 의미를 둘 수 있을 것 같습니다. 글을 다 쓰고 나서 시간이 날때마다 교정하기는 했는데 그래도 오타나 비문이 있을 수 있겠습니다.

댓글남기기