행렬의 직교대각화

2020년 3월, 대학원의 두번째 학기에 행렬의 직교대각화(orthogonal diagonalization)에 대해 고민했습니다. 해당 내용은 수학과 기준 학부 2학년 2학기에 배워야 하는 내용이지만, 그리고 해당 시기의 〈선형대수2〉 과목은 A+을 받기는 했지만, 완벽하게 직교대각화에 대해 이해하지는 못했습니다. 개별적인 행렬의 직교대각화는 할 줄 알았고, eigenvalue-eigenvector가 뭔지 알았지만,

• real symmetric 행렬은 왜 orthogonally diagonalizable한지
• complex Hermitian 행렬은 왜 unitarily diagonalizable한지

에 대해서는 정확하게 이해하지 못했습니다.

그리하여, 한 번 시간을 잡고 위의 두 내용에 대해 고민해본 적이 있습니다. 많은 자료들을 뒤졌지만 정작 제가 궁금해하는 저 위의 사실에 대하여 AtoZ로 알려주는 자료는 찾지 못했습니다. 그래서, 관련 내용을 직접 TeX으로 정리해 본 적이 있습니다. 링크

해당 파일은 영어로 작성해본 것인데, 이번 포스트에서는 이것을 한글로 적으면서 내용도 풀어서 다시 정리해보고자 합니다. 사실, 어느 정도 선형대수에 대한 지식이 있다면, 간결하게 적어놓은 원래 파일이 더 잘 읽힐 수 있습니다.

참고
이 포스트는 기본적으로 한글을 사용하지만, 사용된 수학 용어들은 대부분 영어로 적었습니다. 용어가 처음 등장할 때에 한해서만 한글 표현을 병기해보았습니다. 다만, 고등학교 수준의 수학 용어는 그냥 한국어 용어로 썼습니다.

많은 내용을 한 포스트에 담았습니다. 페이지를 넘기면서 내용을 보는 것 보다는 단지 스크롤과 하이퍼링크만을 사용해 내용을 보는 것이 읽는 입장에서도 편하다고 생각했고 쓰면서 검수하는 입장에서도 편했기 때문입니다. 하지만, 내용이 너무 많다보니 페이지의 모든 수식이 완전히 조판되는 데에는 조금 시간이 걸릴 수 있습니다.

1 정의

1.1 행렬

이 포스트에서 다루는 행렬들은 모두 성분(entry)들이 실수 혹은 복소수인 행렬들만을 다룹니다. 즉, 여기에서 행렬(matrix)이란, 실수 혹은 복소수들을 직사각형 모양으로 배열해 괄호로 묶어 놓은 것을 말합니다. 예를 들어,

\[P=\begin{bmatrix}1&2\\0&2\end{bmatrix},\qquad Q=\begin{bmatrix}0&1&0\\1&0&0\end{bmatrix}\]

는 행렬입니다.

참고

• 개별적인 행렬들은 $P$, $Q$, $R$, $\cdots$ 등으로 적었고, 일반적인 행렬은 $A$, $B$, $C$ 등으로 적었습니다.
• 개별적인 벡터들은 $u$, $v$, $w$ 등으로 적었고, 일반적인 벡터는 $x$, $y$ 등으로 적었습니다.

이때, $P$는 2개의 행과 2개의 열로 이루어진 행렬이어서 ‘$2\times 2$ 행렬’이라고 부르고 $Q$는 2개의 행과 3개의 열로 이루어진 행렬이어서 ‘$2\times3$ 행렬’이라고 부릅니다. 이 포스트에서는 $2\times 2$, $2\times 3$ 등을 그 행렬의 모양이라고 하겠습니다.

행이 하나인 행렬과 열이 하나인 행렬도 행렬로 취급합니다. 이것들은 각각 ‘행벡터’, ‘열벡터’ 라는 이름으로도 불립니다. 예를 들어

\[R=\begin{bmatrix}2&4\end{bmatrix},\qquad S=\begin{bmatrix}1\\-1\\0\end{bmatrix}\]

이면 $R$는 $1\times2$ 행렬이기도 하지만 2차원의 행벡터라고도 불리고, $S$는 $3\times1$ 행렬이기도 하지만 3차원의 열벡터라고도 불립니다.

선형대수를 말할 때 흔히 그렇듯이, 이 포스트에서도 벡터는 열벡터로 표시합니다. 그러니까, 고등학교 수학에서는 $v=(2,1)$을 2차원 벡터, $w=(1,0,3)$을 3차원 벡터로 생각했었습니다. 그런데 선형대수에서는 보통 이것들을 열벡터로 쓰고

\[v=\begin{bmatrix}2\\1\end{bmatrix},\qquad w=\begin{bmatrix}1\\0\\3\end{bmatrix}\]

와 같이 나타내게 됩니다.

행렬을 대문자 알파벳으로 표시한다면, 이 행렬의 성분들은 소문자 알파벳과 두 개의 아래첨자로 표시합니다. 이때 첫번째 아래첨자는 행 번호를, 두번째 아래첨자는 열 번호를 각각 의미합니다. 예를 들어, 위의 행렬

\[P=\begin{bmatrix}1&2\\0&2\end{bmatrix}\]

에서

\[p_{11}=1,\quad p_{12}=2,\quad p_{21}=0,\quad p_{22}=2\]

입니다.

가끔씩은, 행렬 자체에 아래첨자를 주어 행렬의 성분을 표시하기도 합니다. 즉, 행렬 $A$가 주어졌을 때 이 행렬의 $i$행 $j$열 성분은 보통 $a_{ij}$로 나타내지만, $A_{ij}$로 나타내기도 합니다. 이것은 행렬 자체의 표현이 조금 복잡할 때 많이 쓰입니다. 만약 $AB+C$라는 행렬의 $i$행 $j$열 성분을 표현하고 싶다면 $\left(AB+C\right)_{ij}$라고 표현하는 것입니다.

어떤 행렬을 나타낼 때, 행렬의 성분을 소괄호로 감싸고, 거기에 다시 아래첨자로 행렬의 모양을 특정해 표시하기도 합니다. 즉

\[A=(a_{ij})_{m\times n}\]

이면, 이것은 이 행렬 $A$가 $m\times n$ 행렬이고, 그 성분이 $a_{ij}$라는 뜻입니다. 예를 들어,

\[T=\left(t_{ij}\right)_{2\times2}=\left(i+j-1\right)_{2\times2}\]

이면

\[T=\begin{bmatrix}1&2\\2&3\end{bmatrix}\]

이 될 것입니다.

여러가지 행렬

어떤 행렬의 행의 개수와 열의 개수가 같으면 그 행렬을 정사각행렬(정방행렬, square matrix)이라고 부릅니다. 예를 들어, $P$, $T$는 정사각행렬이지만 $Q$, $R$, $S$는 정사각행렬이 아닙니다.

어떤 행렬 $A$에 대하여, $A$의 대각성분이란 $i=j$를 만족시키는 $a_{ij}$들을 말합니다. 만약 대각성분들을 제외한 모든 성분들이 0이면, 이 행렬을 대각행렬이라고 부릅니다.

예를 들어,

\[D=\begin{bmatrix}2&0\\0&5\end{bmatrix},\qquad E=\begin{bmatrix}1&0&0\\0&0&0\\0&0&2\end{bmatrix},\qquad F=\begin{bmatrix}-1&0&0\\0&4&0\end{bmatrix}\]

와 같은 행렬들은 대각행렬입니다. 반면, 위에서 정의한 $P$, $Q$, $R$, $S$, $T$는 모두 대각행렬이 아닙니다.

대각행렬 중 가장 간단하면서 중요한 행렬은 항등행렬이라고 불리는 행렬입니다. 항등행렬은, 정사각행렬 중에서 대각성분이 모두 1인 대각행렬을 말합니다. 즉,

\[\begin{bmatrix}1&0\\0&1\end{bmatrix},\quad\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix},\quad\cdots\]

와 같은 행렬을 말합니다. 항등행렬의 행의 수(=열의 수)가 $n$개이면 그 항등행렬을 $I_n$으로 표현합니다. ($n$이 중요하지 않다면 $n$를 생략하여 그냥 $I$라고 쓸 수도 있습니다.) 즉, 위의 항등행렬들은

\[I_2=\begin{bmatrix}1&0\\0&1\end{bmatrix},\quad I_3=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix},\quad\\ \cdots\]

와 같이 표현될 수 있습니다.

두 정사각행렬 $A$, $B$에 대하여

\[AB=BA=I\]

가 성립하면 $B$를 $A$의 역행렬이라고 말하고, $B=A^{-1}$라고 씁니다. 반대로, $A$는 $B$의 역행렬이기도 합니다. 즉 $A=B^{-1}$이기도 합니다. 따라서 $A$의 역행렬이 존재하면

\[AA^{-1}=A^{-1}A=I\]

입니다. 역행렬이 존재하는 행렬을 가역행렬(invertible matrix)이라고 부릅니다.

참고
두 정사각행렬 $A$, $B$에 대하여 $AB=I$이면 $BA=I$가 성립합니다.
이것은 당연한 말 같아보이기는 해도, 쉽게 증명되지는 않습니다. 뒤에 나오는 정리 14(a)를 사용하면 determinant를 사용하여 증명 할 수 있습니다. 만약, 정사각행렬들의 집합이 algebra over a field 라는 사실을 사용하면 선형대수의 다른 개념들을 많이 사용하지 않고도 증명 할 수 있습니다.
여하튼, 이것을 적용하면 다음과 같이 쓸 수 있습니다. 두 정사각형 $A$, $B$에 대하여 $AB=I$이면 $B=A^{-1}$ 입니다.

1.2 행렬의 연산

이항연산

두 행렬의 모양이 같으면 두 행렬을 더할 수 있습니다. 두 행렬을 더할 때에는 성분별로 더하면 됩니다. 예를 들어, $P$와 $T$는 모양이 서로 같으므로 서로 더할 수 있고, 그 결과가

\[P+T=\begin{bmatrix}1&2\\0&2\end{bmatrix}+\begin{bmatrix}1&2\\2&3\end{bmatrix}=\begin{bmatrix}1+1&2+2\\0+2&2+3\end{bmatrix}=\begin{bmatrix}2&4\\2&5\end{bmatrix}\]

로 나타나지만, $P$와 $Q$는 모양이 서로 다르므로 더할 수 없습니다.

두 행렬에 대해서 첫번째 행렬의 열의 수와 두번째 행렬의 행의 수가 같으면 두 행렬을 곱할 수 있습니다. 그러니까, $A$가 $m\times n$ 행렬이고, $B$가 $n\times l$ 행렬이면, 두 행렬 $A$, $B$의 곱 $AB$를 생각할 수 있습니다. 이때, $AB$의 성분은

\[\left(AB\right)_{ij}=\sum_{k=1}^na_{ik}b_{kj}\]

입니다.

예를 들어, $P$와 $Q$는 각각 $2\times2$, $2\times3$ 행렬이고 따라서 두 행렬을 곱할 수 있습니다. ($m=2$, $n=2$, $l=3$) 그 결과는

\[\begin{align*} PQ &=\begin{bmatrix}1&2\\0&2\end{bmatrix}\begin{bmatrix}0&1&0\\1&0&0\end{bmatrix}\\ &=\begin{bmatrix} 1\times0+2\times1&1\times1+2\times0&1\times0+2\times0\\ 0\times0+2\times1&0\times1+2\times0&0\times0+2\times0 \end{bmatrix}\\ &=\begin{bmatrix} 2&1&0\\ 2&0&0 \end{bmatrix} \end{align*}\]

입니다.

마찬가지로,

\[\begin{align*} PT&=\begin{bmatrix}1&2\\0&2\end{bmatrix}\begin{bmatrix}1&2\\2&3\end{bmatrix}=\begin{bmatrix}5&8\\4&6\end{bmatrix}\\ QS&=\begin{bmatrix}0&1&0\\1&0&0\end{bmatrix}\begin{bmatrix}1\\-1\\0\end{bmatrix}=\begin{bmatrix}-1\\1\end{bmatrix}\\ RP&=\begin{bmatrix}2&4\end{bmatrix}\begin{bmatrix}1&2\\0&2\end{bmatrix}=\begin{bmatrix}2&12\end{bmatrix}\\ P^2&=\begin{bmatrix}1&2\\0&2\end{bmatrix}^2=\begin{bmatrix}1&2\\0&2\end{bmatrix}\begin{bmatrix}1&2\\0&2\end{bmatrix} =\begin{bmatrix}1&6\\0&4\end{bmatrix} \end{align*}\]

와 같이 계산할 수 있습니다. 이상은 행렬이 두 개 주어졌을 때 만들 수 있는 이항연산인 덧셈과 곱셈입니다.

단항연산

행렬 하나에 대해서도 연산을 정의할 수 있는데, 대표적인 것이 transpose (전치)와 conjugate transpose (켤레전치)입니다.

행렬 $A$에 대하여, $A$의 transpose는 $A^T$와 같이 표시하는데, 이것은 $A$의 대각성분을 기준으로 양옆을 뒤집어놓은 행렬입니다. 예를 들면,

\[\begin{align*} P^T&=\begin{bmatrix}1&2\\0&2\end{bmatrix}^T=\begin{bmatrix}1&0\\2&2\end{bmatrix}\\ Q^T&=\begin{bmatrix}0&1&0\\1&0&0\end{bmatrix}^T=\begin{bmatrix}0&1\\1&0\\0&0\end{bmatrix}\\ R^T&=\begin{bmatrix}2&4\end{bmatrix}^T=\begin{bmatrix}2\\4\end{bmatrix} \end{align*}\]

등입니다. $A=\left(a_{ij}\right)_{m\times n}$의 transpose $A^T$를 다음과 같이 정의할 수도 있습니다.

\[A^T=\left(a_{ji}\right)_{n\times m}\]

conjugate transpose에 대해 설명하기 전에 conjugation(켤레복소수화, 공액)에 대해 먼저 이야기하겠습니다. 어떤 복소수 $z=a+bi$에 대하여 ($a$, $b$는 실수) 이 복소수의 켤레복소수는 $a-bi$이고, 이것을 $\bar z$로 표시합니다. 이와 같이, 주어진 복소수를 그 켤레복소수(conjugate)로 변환하는 연산을 conjugation이라고 합니다.

예를 들어

\[\begin{align*} \overline{2+3i}&=2-3i\\ \overline{2-3i}&=2+3i\\ \overline{i}&=-i\\ \overline{3}&=3\\ \overline{\frac{i-2}3}&=\frac{-i-2}3\\ \end{align*}\]

입니다. 이때, 실수의 켤레복소수가 자기 자신이 된다는 것은 중요합니다.

$z$가 실수이면, $\bar z=z$이고, 그 역도 성립합니다.

이에 대한 증명은 간단합니다. 복소수 $z=a+bi$에 대하여, 만약 $z$가 실수이면 $b=0$이고, $\bar z=\overline{a+0i}=a-0i=z$입니다. 반대로,$\bar z=z$이면 $a+bi=a-bi$입니다. 두 복소수가 같으려면 실수부분과 허수부분이 서로 같아야 하므로 $b=-b$, $2b=0$, $b=0$입니다. 따라서 $z$는 실수입니다. $\square$

conjugation은 단순히 복소수에 대해서만이 아니라, 복소수를 성분으로 가지는 행렬에 대해서도 취할 수 있습니다. 행렬 $A$에 대하여 $A$의 conjugate은 $\bar A$로 표시하며, $A$의 각 성분들에 conjugation을 취한 행렬로 정의합니다;

\[\bar A = \left(\overline{a_{ij}}\right)_{m\times n}\]

예를 들어 복소수를 성분으로 갖는 행렬 $Z$가

\[Z=\begin{bmatrix}0&2-3i\\2+3i&3\end{bmatrix}\]

와 같이 정의될 때,

\[\begin{align*} \overline Z &=\begin{bmatrix}\overline 0&\overline{2-3i}\\\overline{2+3i}&\overline3\end{bmatrix}\\ &=\begin{bmatrix}0&2+3i\\2-3i&3\end{bmatrix} \end{align*}\]

인 것입니다. 복소행렬의 conjugation에 대해서도 위의 명제와 비슷한 명제가 성립합니다;

$A$가 실수로 이루어진 행렬이면, $\bar A=A$이고, 그 역도 성립합니다.

만약, $A$가 실수로 이루어진 행렬이면,

\[\bar A = \left(\overline{a_{ij}}\right)_{m\times n} = \left(a_{ij}\right)_{m\times n} = A\]

입니다. 반대로, $\bar A=A$이면, 모든 $i$, $j$에 대하여 $\overline{a_{ij}}=a_{ij}$가 성립한다는 뜻입니다. 따라서 $a_{ij}$들은 모두 실수입니다. $\square$

지금까지 정의한 행렬 $P$, $Q$, $R$, $S$, $T$, $Z$에서 위의 사실을 간단히 확인해볼 수 있습니다. $P$, $Q$, $R$, $S$, $Z$는 실수로 이루어진 행렬들이고 따라서 $\overline P=P$, $\overline Q=Q$, $\overline R=R$, $\overline S=S$, $\overline T=T$가 성립합니다. $Z$는 실수로만 이루어진 행렬이 아니고, 허수가 포함된 행렬입니다. 따라서 $\bar Z\neq Z$입니다.

이제 행렬의 conjugate transpose를 정의할 수 있습니다. 어떤 행렬 $A$의 conjugate transpose는 $A^H$와 같이 표시하는데, 이것은 $A$를 transpose하고, conjugation한 것을 말합니다. 즉,

\[A^H=\overline{A^T}\]

입니다. 그런데, 사실 transpose를 먼저 취하나, conjuagtion을 먼저 취하나 그 결과는 같으므로

\[A^H = \bar A^T\]

와 같이 정의해도 정확히 같은 정의가 됩니다.

한편, 실수로 이루어진 행렬 $A$에 대하여는 transpose를 취하는 것과 conjugate transpose를 취하는 것에는 차이가 없습니다 ;

\[A^H=\overline{\left(a_{ij}\right)_{n\times n}\,^T} =\overline{\left(a_{ji}\right)_{n\times n}} =\left(\overline{a_{ji}}\right)_{n\times n} =\left(a_{ji}\right)_{n\times n} =A^T\]

또한, 두 행렬 $A$, $B$의 곱 $AB$에 대하여 transpose나 conjugate transpose를 취한 결과는 각 행렬을 transpose 혹은 conjugate transpose한 후 순서를 바꾸어 곱한 결과와 같습니다 ;

\[\begin{align*} \left((AB)^T\right)_{ij} &=\left(AB\right)_{ji} =\sum_{k=1}^na_{jk}b_{ki}\\ &=\sum_{k=1}^m{B^T}_{ik}{A^T}_{kj} =\left(B^TA^T\right)_{ij} \\ \left(\overline{AB}\right)_{ij} &=\overline{\left(AB\right)_{ij}} =\overline{\sum_{k=1}^na_{ik}b_{kj}}\\ &=\sum_{k=1}^n\overline{a_{ik}}\overline{b_{kj}} =\left(\overline A\;\overline B\right)_{ij}\\ (AB)^H &=\left(\overline{AB}\right)^T =\left(\overline A\overline B\right)^T =\overline B^T\overline A^T =B^HA^H \end{align*}\]

이상을 정리하면 다음과 같습니다.

정의 01 : 행렬의 연산
정사각행렬 $A=\left(a_{ij}\right)_{n\times n}$, $B=\left(b_{ij}\right)_{n\times n}$와 실수 $c$에 대하여
(a) $A+B=\left(a_{ij}+b_{ij}\right)_{n\times n}$
(b) $A-B=\left(a_{ij}-b_{ij}\right)_{n\times n}$
(c) $AB=\left(\sum_{k=1}^na_{ik}b_{kj}\right)_{n\times n}$
(d) $cA=\left(ca_{ij}\right)_{n\times n}$
(e) $A^T=\left(a_{ji}\right)_{n\times n}$
(f) $A^H=\left(\overline{a_{ji}\,}\right)_{n\times n}$

(a)에서 정의된 행렬의 덧셈은 결합법칙과 교환법칙을 만족시킵니다 ; $(A+B)+C=A+(B+C)$, $(AB)C=A(BC)$. (c)에서 정의된 행렬의 곱셈은 결합법칙을 만족시키지만 교환법칙을 만족시키지는 않습니다 ; $(AB)C=A(BC)$. 덧셈과 곱셈에 대해서 분배법칙도 성립합니다 ; $(A+B)C=AB+BC$, $A(B+C)=AB+AC$. (d)에서 정의되는 연산을 스칼라곱(scalar multiplication)이라고 부릅니다. 이때 $c$는 스칼라(scalar)라고 부르며 이것은 실수 (혹은 복소수)를 의미합니다. 스칼라곱에 대해서 분배법칙과 비슷한 성질들이 성립합니다 ; $(c_1+c_2)A=c_1A+c_2A$, $c(A+B)=cA+cB$.

성질 02
정사각행렬 $A=\left(a_{ij}\right)_{n\times n}$, $B=\left(b_{ij}\right)_{n\times n}$에 대하여
(a) $A$가 실수로 이루어진 행렬이면 $\overline A=A$가 성립하고 그 역도 성립합니다.
(b) $A$가 실수로 이루어진 행렬이면 $A^H=A^T$가 성립하고 그 역도 성립합니다.
(c) $(AB)^T=B^TA^T$, $\overline{AB}=\overline A\;\overline B$, $(AB)^H=B^HA^H$
(d) $(A^T)^T=A$, $(A^H)^H=A$
(e) $A$, $B$의 역행렬이 존재하면 $(AB)^{-1}=B^{-1}A^{-1}$ 입니다.

1.3 symmetric / Hermitian

이제, 이 포스트에서 목표로 하는 두 명제에 등장하는 두 표현인 ‘symmetric’과 ‘Hermitian’을 정의할 수 있습니다.

symmetric 행렬

symmetric 행렬 (symmetric matrix, 대칭 행렬)이란, 행렬의 대각성분들을 기준으로 양옆이 대칭인 행렬을 말합니다. 예를 들어 행렬

\[T=\begin{bmatrix}1&2\\2&3\end{bmatrix}\]

의 대각성분들은 $t_{11}=1$, $t_{22}=3$인데 이것들을 기준으로 양옆이 대칭입니다. 따라서 $T$는 symmetric 행렬입니다. 반면, 행렬

\[P=\begin{bmatrix}1&2\\0&2\end{bmatrix},\qquad Q=\begin{bmatrix}0&1&0\\1&0&0\end{bmatrix}\]

는 대각성분들을 기준으로 대칭이 아니므로 symmetric 행렬이 아닙니다. $Q$와 같은 $2\times 3$ 행렬은 어떻게 해도 symmetric하지 않습니다. 즉, symmetric 행렬이 되기 위해서는 일단 그 행렬이 정사각행렬일 필요가 있습니다.

행렬의 symmetricity는 transpose를 사용하면 쉽게 정의할 수도 있습니다.

정의 03
행렬 $A$에 대하여 $A^T=A$이면 $A$를 symmetric 행렬이라고 부릅니다.

Hermitian 행렬

한편, Hermitian 행렬(Hermitian matrix, 에르미트 행렬)이란, 대각 성분들을 기준으로 양옆이 서로 켤레관계인 행렬을 말합니다. 이것을 conjugate transpose로 표현하면 다음과 같이 간단하게 정의할 수 있습니다.

정의 04
행렬 $A$에 대하여 $A^H=A$이면 $A$를 Hermitian 행렬이라고 부릅니다.

symmetric 행렬에서와 마찬가지로, 어떤 행렬이 Hermitian이기 위해서는 일단 정사각행렬이어야 합니다. $P$, $Q$, $R$, $S$, $T$, $Z$ 중에서 정사각행렬인 것은

\[\begin{align*} P&=\begin{bmatrix}1&2\\0&2\end{bmatrix}\\ T&=\begin{bmatrix}1&2\\2&3\end{bmatrix}\\ Z&=\begin{bmatrix}0&2-3i\\2+3i&3\end{bmatrix} \end{align*}\]

입니다. 이 중에서 $T$, $Z$는 Hermitian 행렬이고, $P$는 Hermite 행렬이 아닙니다. $P$, $T$는 실수로 이루어진 행렬이므로 성질 3(b)를 사용하여

\[\begin{align*} P^H&=P^T\ne P\\ T^H&=T^T=T \end{align*}\]

임을 확인할 수 있습니다. $Z$에 대해서는 직접 complex conjugate를 계산하여

\[Z^H =\overline{Z^T}=\overline{\begin{bmatrix}0&2+3i\\2-3i&3\end{bmatrix}} =\begin{bmatrix}\bar0&\overline{2+3i}\\\overline{2-3i}&\bar3\end{bmatrix}=Z\]

와 같이 계산할 수 있습니다.

1.4 orthogonal / unitary

inner product / norm

고등학교 수학에 따르면, 2차원 벡터 $x$, $y$가 다음과 같이 주어져 있을 때,

\[x=\begin{bmatrix}x_1\\x_2\end{bmatrix},\quad y=\begin{bmatrix}y_1\\y_2\end{bmatrix}\]

두 벡터의 내적 $x\cdot y$은

\[x\cdot y=x_1y_1+x_2y_2\]

로 정의됩니다. 또한, 벡터 $x$의 길이는

\[\sqrt{x_1\,^2+x_2\,^2}\]

으로 나타낼 수 있었습니다. 고등학교 수학에서는 3차원까지 다룹니다. 3차원 벡터 $x$, $y$가

\[x=\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix},\quad y=\begin{bmatrix}y_1\\y_2\\y_3\end{bmatrix}\]

와 같이 주어질 때, 두 벡터의 내적은

\[x\cdot y=x_1y_1+x_2y_2+x_3y_3\]

이고, $x$의 길이는

\[\sqrt{x_1\,^2+x_2\,^2+x_3\,^2}\]

입니다.

이것을 일반적인 $n$차원으로 확장하면, 두 벡터

\[x=\begin{bmatrix}x_1\\x_2\\\vdots\\x_n\end{bmatrix},\quad y=\begin{bmatrix}y_1\\y_2\\\vdots\\y_n\end{bmatrix}\]

에 대하여 $x$와 $y$의 내적은

\[x\cdot y=\sum_{k=1}^nx_ky_k\]

으로, $x$의 길이는

\[\sqrt{\sum_{k=1}^n{x_k}^2}\]

으로 정할 수 있을 것입니다.

이것이, $n$차원 벡터의 내적(inner product)과 놈(norm)에 해당합니다. 더 정리해서 말하기 전에, 열벡터로서 표현된 두 벡터의 $x$, $y$의 내적과 norm을 행렬곱의 형식으로 표현해보려 합니다. 위의 정의된 $x\cdot y$의 식은 행렬곱의 정의에 의해 $x^Ty$와 같습니다;

\[\begin{align*} x^Ty &=\begin{bmatrix}x_1&x_2&\cdots&x_n\end{bmatrix}\begin{bmatrix}y_1\\y_2\\\vdots\\y_n\end{bmatrix}\\ &=x_1y_1+x_2y_2+\cdots+x_ny_n=x\cdot y. \end{align*}\]

한편, $x$의 크기는 $x$와 그 자신의 내적, 즉 $x^Tx$에 루트를 씌운 값과 같습니다;

\[\sqrt{x^Tx}=\sqrt{x_1\,^2+x_2\,^2+\cdots+x_n}\,^2=\sqrt{\sum_{k=1}^n{x_k}^2}\]

이 포스트에서는 내적을 표현할 때 $x\cdot y$라는 표현 대신 $\langle x,y\rangle$라는 표현을 쓰겠습니다. 또한 $x$의 크기는 $||x||$로 표시하며, ‘크기’라는 표현 대신 ‘norm’이라는 표현을 사용하겠습니다.

정의 05
(a) $n$차원 실수 벡터 $x$, $y$에 대하여 $x$와 $y$의 내적 은 $$\langle x,y\rangle=x^Ty$$ 입니다.
(b) $n$차원 실수 벡터 $x$의 norm 은 $$||x||=\sqrt{\langle x,x\rangle}=\sqrt{x^Tx}$$ 입니다.

orthogonal / orthonormal

고등학교 수학에서, 영벡터가 아닌 두 벡터가 서로 수직(orthogonal)이면 그 내적이 0이며, 그 역도 성립한다는 것을 다룹니다.

예를 들어, 세 개의 2차원 벡터 $u_1$, $u_2$, $u_3$가

\[u_1=\begin{bmatrix}1\\-2\end{bmatrix},\quad u_2=\begin{bmatrix}2\\1\end{bmatrix},\quad u_3=\begin{bmatrix}1\\0\end{bmatrix}\]

이면

$u_1$와 $u_2$는 서로 수직입니다($u_1\perp u_2$);

\[{u_1}^Tu_2=\begin{bmatrix}1&-2\end{bmatrix}\begin{bmatrix}2\\1\end{bmatrix}=0\]

하지만 $u_1$와 $u_3$, $u_2$와 $u_3$는 수직이 아닙니다($u_1\not\perp u_3$, $u_2\not\perp u_3$);

\[\begin{align*} {u_1}^Tu_3&=\begin{bmatrix}1&-2\end{bmatrix}\begin{bmatrix}1\\0\end{bmatrix}=1\neq0\\ {u_2}^Tu_3&=\begin{bmatrix}2&1\end{bmatrix}\begin{bmatrix}1\\0\end{bmatrix}=2\neq0\\ \end{align*}\]

한편, 세 개의 3차원 벡터 $v_1$, $v_2$, $v_3$가

\[v_1=\begin{bmatrix}1\\-2\\0\end{bmatrix},\quad v_2=\begin{bmatrix}2\\1\\0\end{bmatrix},\quad v_3=\begin{bmatrix}0\\0\\1\end{bmatrix}\]

이면

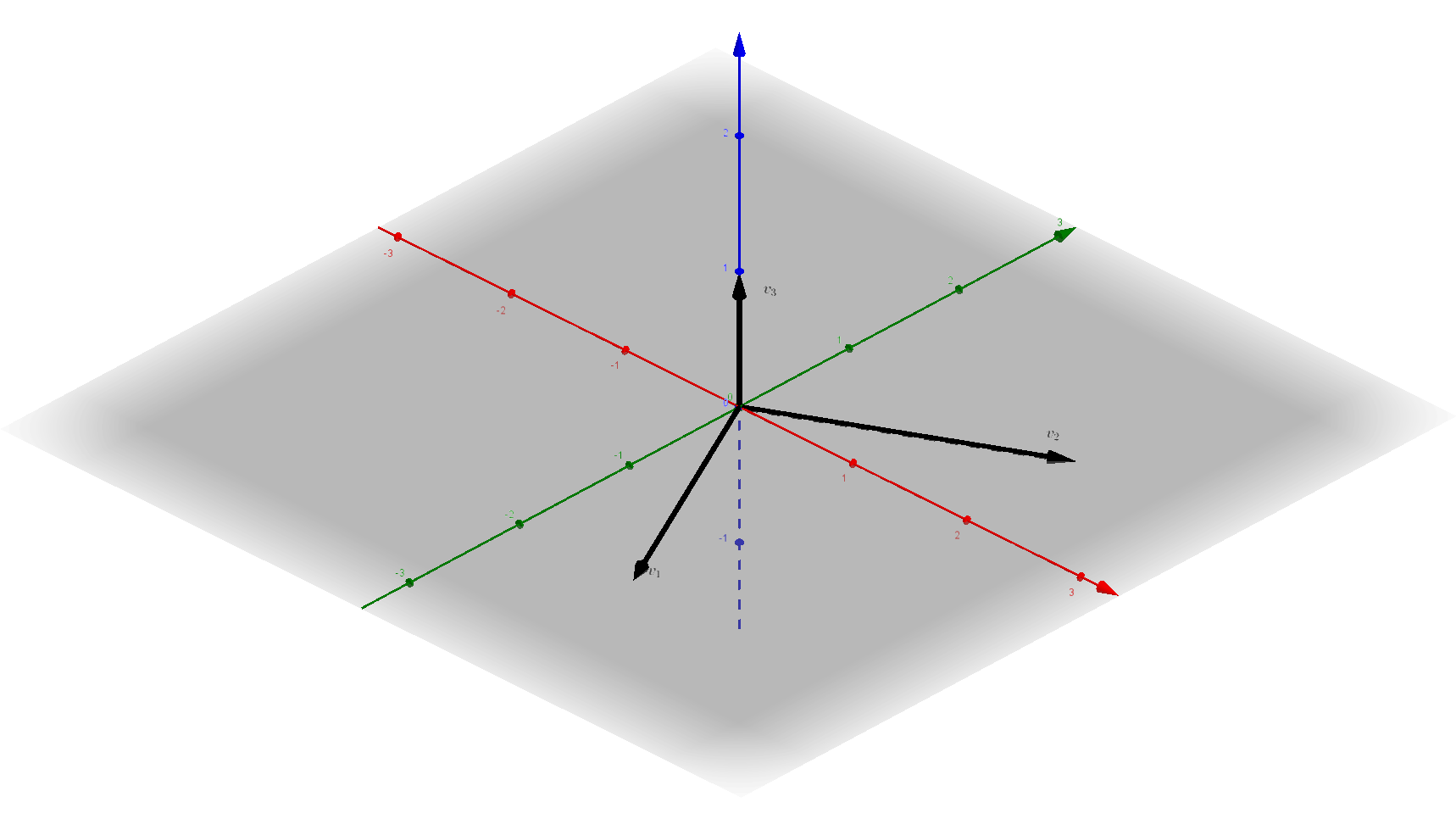
$v_1$와 $v_2$, $v_1$와 $v_3$, $v_2$와 $v_3$는 모두 서로 수직입니다($v_1\perp v_2$, $v_1\perp v_3$, $v_2\perp v_3$);

\[\begin{align*} {v_1}^Tv_2&=\begin{bmatrix}1&-2&0\end{bmatrix}\begin{bmatrix}2\\1\\0\end{bmatrix}=0\\ {v_1}^Tv_3&=\begin{bmatrix}1&-2&0\end{bmatrix}\begin{bmatrix}0\\0\\1\end{bmatrix}=0\\ {v_2}^Tv_3&=\begin{bmatrix}2&1&0\end{bmatrix}\begin{bmatrix}0\\0\\1\end{bmatrix}=0 \end{align*}\]

이때, $v_1$, $v_2$, $v_3$의 경우처럼 벡터들이 모두 서로 수직일때, 이 벡터들이 pairwisely orthogonal (mutually orthogonal) 하다고 말합니다. 위의 예에서 $u_1$, $u_2$, $u_3$는 pairwisely orthogonal하지 않고, $v_1$, $v_2$, $v_3$는 pairwisely orthogonal합니다.

이번에는 $v_1$, $v_2$, $v_3$를 조금 변형해서 $w_1$, $w_2$, $w_3$를 다음과 같이 만들면

\[w_1=\begin{bmatrix}\frac1{\sqrt5}\\-\frac2{\sqrt5}\\0\end{bmatrix},\quad w_2=\begin{bmatrix}\frac2{\sqrt5}\\\frac1{\sqrt5}\\0\end{bmatrix},\quad w_3=\begin{bmatrix}0\\0\\1\end{bmatrix}\]

이 경우에도 $w_1\perp u_2$, $w_1\perp w_3$, $w_2\perp w_3$가 성립합니다. 즉 $w_1$, $w_2$, $w_3$은 pairwisely orthogonal합니다. 여기에 더해, 그 벡터들의 크기가 1이라는 성질이 있습니다;

\[\begin{align*} ||w_1||&=\sqrt{\left(\frac1{\sqrt5}\right)^2+\left(-\frac2{\sqrt5}\right)^2+0^2}=1\\ ||w_2||&=\sqrt{\left(\frac2{\sqrt5}\right)^2+\left(\frac1{\sqrt5}\right)^2+0^2}=1\\ ||w_3||&=\sqrt{0^2+0^2+1^2}=1 \end{align*}\]

이런 경우에, 이 벡터들이 orthonormal하다고 말합니다.

정리하면 다음과 같습니다.

정의 06
(a) 두 실수 벡터 $x$, $y$에 대하여 $$x^Ty=0$$ 이면 두 벡터가 orthogonal하다(수직이다)고 말하고, $x\perp y$라고 표현합니다.
(b) $n$개의 실수 벡터 $x_1$, $x_2$, $\cdots$, $x_n$에 대하여 $${x_i}^Tx_j=0\quad(i\neq j)$$ 이면, 이 벡터들이 pairwisely orthogonal하다고 말합니다.
(c) $n$개의 실수 벡터 $x_1$, $x_2$, $\cdots$, $x_n$에 대하여 $$ {x_i}^Tx_j= \begin{cases}0&(i\neq j)\\1&(i=j)\end{cases} $$ 이면, 이 벡터들이 orthonormal하다고 말합니다.

orthogonal 행렬

orthogonal한 세 개의 3차원벡터 $v_1$, $v_2$, $v_3$에 대해 다시 생각해봅시다.

\[v_1=\begin{bmatrix}1\\-2\\0\end{bmatrix},\quad v_2=\begin{bmatrix}2\\1\\0\end{bmatrix},\quad v_3=\begin{bmatrix}0\\0\\1\end{bmatrix}\]

$v_i$로 만들 수 있는 모든 조합의 내적을 나열해보면

\[\begin{align*} {v_1}^Tv_1 = 5 &&{v_1}^Tv_2 = 0 &&{v_1}^Tv_3 = 0 \\ {v_2}^Tv_1 = 0 &&{v_2}^Tv_2 = 5 &&{v_2}^Tv_3 = 0 \\ {v_3}^Tv_1 = 0 &&{v_3}^Tv_2 = 0 &&{v_3}^Tv_3 = 1 \end{align*}\]

이 됩니다. 재밌는 사실은, 이 아홉 개의 계산을 하나의 행렬곱으로 표현할 수 있다는 것입니다. 행렬곱의 정의를 상기해보면

\[\begin{bmatrix} 1&-2&0\\ 2&1&0\\ 0&0&1 \end{bmatrix} \begin{bmatrix} 1&2&0\\ -2&1&0\\ 0&0&1 \end{bmatrix} = \begin{bmatrix} 5&0&0\\ 0&5&0\\ 0&0&1 \end{bmatrix}\]

와 같이 표현할 수 있는 것입니다. 위 식의 좌변의 첫번째 행렬은 세 행벡터 ${v_1}^T$, ${v_2}^T$, ${v_3}^T$를 세로로 쌓아놓은 것이고, 두번째 행렬은 세 열벡터 $v_1$, $v_2$, $v_3$를 가로로 나열한 것입니다. 즉,

\[\begin{bmatrix} -&{v_1}^T&-\\ -&{v_2}^T&-\\ -&{v_3}^T&- \end{bmatrix} \begin{bmatrix} |&|&|\\ v_1&v_2&v_3\\ |&|&| \end{bmatrix} = \begin{bmatrix} 5&0&0\\ 0&5&0\\ 0&0&1 \end{bmatrix}\]

입니다. 이때, 세 열벡터 $v_1$, $v_2$, $v_3$를 가로로 나열한 행렬을 $V$로 표기하면 위의 식을 간단히

\[V^TV= \begin{bmatrix} 5&0&0\\ 0&5&0\\ 0&0&1 \end{bmatrix}\]

로 쓸 수 있습니다. 일반적으로, 정사각행렬 $A$가 pairwisely orthogonal한 벡터들을 가로로 나열한 행렬이면, $A^TA$는 대각행렬입니다.

이번에는 orthonormal한 세 개의 3차원벡터 $w_1$, $w_2$, $w_3$에 대해 다시 생각해봅시다.

\[w_1=\begin{bmatrix}\frac1{\sqrt5}\\-\frac2{\sqrt5}\\0\end{bmatrix},\quad w_2=\begin{bmatrix}\frac2{\sqrt5}\\\frac1{\sqrt5}\\0\end{bmatrix},\quad w_3=\begin{bmatrix}0\\0\\1\end{bmatrix}\]

아까처럼, $w_i$로 만들 수 있는 모든 조합의 내적을 나열해보면

\[\begin{align*} {w_1}^Tv_1 = 1 &&{w_1}^Tv_2 = 0 &&{w_1}^Tv_3 = 0 \\ {w_2}^Tv_1 = 0 &&{w_2}^Tv_2 = 1 &&{w_2}^Tv_3 = 0 \\ {w_3}^Tv_1 = 0 &&{w_3}^Tv_2 = 0 &&{w_3}^Tv_3 = 1 \end{align*}\]

이고

\[\begin{bmatrix} -&{w_1}^T&-\\ -&{w_2}^T&-\\ -&{w_3}^T&- \end{bmatrix} \begin{bmatrix} |&|&|\\ w_1&w_2&w_3\\ |&|&| \end{bmatrix} = \begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{bmatrix}\]

입니다. 좌변의 두번째 행렬을 $W$로 표기하면

\[W^TW=I\]

가 됩니다. 이때, $W$와 같은 행렬을 orthogonal 행렬이라고 합니다.

정의 07
정사각행렬 $A$가 $$A^TA=I$$ 를 만족시키면 $A$를 orthogonal 행렬(orthogonal matrix, 직교행렬)이라고 부릅니다.

$w_1$, $w_2$, $w_3$와 $W$ 사이의 관계에서 볼 수 있듯 다음의 성질 8(a), 8(b)가 성립합니다. 또한, 1.1의 두번째 참고에 의해 성질 8(c)가 성립합니다.

성질 08
(a) $n$차원의 orthonormal한 실수벡터들 $n$개를 가로로 나열해서 얻은 행렬은 orthogonal 합니다.
(b) $A$가 orthogonal 행렬이면 $A$의 각 열들은 orthonormal 합니다.
(c) $A$가 orthogonal 행렬이면, $A$의 역행렬은 $A$의 transpose와 같습니다 ; $$A^{-1}=A^T$$

참고
이 포스트에서 orthogonal이라는 말은 두 가지 의미를 가집니다. 두 의미를 혼동하지 않고 잘 사용해야 합니다.

• 두 벡터가 orthogonal한 것은 두 벡터를 내적했을 때 0이 된다는 뜻입니다.
• 어떤 정사각행렬이 orthogonal한 것은 각 열들이 orthonormal하다는 뜻입니다. 즉, 역행렬과 transpose가 일치하는 경우입니다.

unitary 행렬

지금까지 정의한 내적, norm, orthogonality 등은 성분이 실수인 벡터 혹은 행렬에 대한 개념입니다. 일반적으로, 성분이 복소수인 벡터 혹은 행렬(복소 벡터, 복소 행렬)에 대해 생각한다면, 그에 따른 내적, norm, orthogonality 등의 개념은 실수일 때와는 조금 다르게 정의됩니다.

정의 09
(a) $n$차원 복소 벡터 $x$, $y$에 대하여 $x$와 $y$의 내적 $\langle x,y\rangle$은 $$\langle x,y\rangle=x^Hy$$ 입니다.
(b) $n$차원 복소 벡터 $x$의 norm $||x||$은 $$||x||=\sqrt{\langle x,x\rangle}=\sqrt{x^Hx}$$ 입니다.

정의 4와 비교해보면 transpose(T)였던 것이 conjugate transpose(H)로 바뀌었습니다. 다시 말해,

\[x=\begin{bmatrix}x_1\\x_2\\\vdots\\x_n\end{bmatrix},\quad y=\begin{bmatrix}y_1\\y_2\\\vdots\\y_n\end{bmatrix}\]

이면 ($x_i$, $y_i$는 복소수),

\[\begin{align*} \langle x, y\rangle &=\overline{x_1}y_1+\overline{x_2}y_2+\cdots+\overline{x_n}y_n=\sum_{k=1}^n\overline{x_k}y_k\\ ||x|| &=\sqrt{|x_1|^2+|x_n|^2+\cdots+|x_n|^2}=\sqrt{\sum_{k=1}^n|x_k|^2} \end{align*}\]

인 것입니다. (복소수 $z=a+bi$에 대하여 $z$의 절댓값 $|z|$는 $|z|=\sqrt{z\bar z}=\sqrt{a^2+b^2}$로 정의됩니다.) 예를 들어, 벡터 $u_1$, $u_2$가

\[u_1=\begin{bmatrix}1+2i\\2-i\end{bmatrix},\quad u_2=\begin{bmatrix}3\\1-i\end{bmatrix}\]

이면

\[\begin{align*} \langle u_1, u_2\rangle % &=\left\langle \begin{bmatrix}1+2i\\2-i\end{bmatrix}, \begin{bmatrix}3\\1-i\end{bmatrix}\right\rangle\\ &={u_1}^Hu_2\\ &=\begin{bmatrix}1-2i&2+i\end{bmatrix}\begin{bmatrix}3\\1-i\end{bmatrix}\\ &=(1-2i)3+(2+i)(1-i)\\ &=(3-6i)+(3-i)=6-7i \end{align*}\]

이고

\[\begin{align*} ||u_1|| &=\sqrt{\,{u_1}^Hu_1}\\ &=\sqrt{\begin{bmatrix}1-2i&2+i\end{bmatrix}\begin{bmatrix}1+2i\\2-i\end{bmatrix}}\\ &=\sqrt{(1-2i)(1+2i)+(2+i)(2-i)}\\ &=\sqrt{5+5}=\sqrt{10}\\ ||u_2|| &=\sqrt{\,{u_2}^Hu_2}\\ &=\sqrt{\begin{bmatrix}3&1+i\end{bmatrix}\begin{bmatrix}3\\1-i\end{bmatrix}}\\ &=\sqrt{3\times3+(1+i)(1-i)}\\ &=\sqrt{11} \end{align*}\]

입니다.

참고
정의 5에서 정의된 실수벡터의 내적 $\langle x,y\rangle=x^Ty$는 좋은 성질들이 많이 성립합니다; $x$, $y$, $z$가 실수벡터이고 $c$가 실수일 때,

• $\langle x,y\rangle=\langle y,x\rangle$
• $\langle x+y,z\rangle=\langle x,z\rangle+\langle y,z\rangle$
• $\langle x,y+z\rangle=\langle x,y\rangle+\langle x,z\rangle$
• $\langle cx,y\rangle=c\langle x,y\rangle=\langle x,cy\rangle$

하지만 정의 9에서 정의된 복소벡터의 내적 $\langle x,y\rangle=x^Hy$에 대해서는, 조금 더 일반적인 다음 성질들이 성립합니다; $x$, $y$, $z$가 복소벡터이고 $c$가 복소수일 때,

• $\langle x,y\rangle=\overline{\langle y,x\rangle}$
• $\langle x+y,z\rangle=\langle x,z\rangle+\langle y,z\rangle$
• $\langle x,y+z\rangle=\langle x,y\rangle+\langle x,z\rangle$
• $\langle cx,y\rangle=\overline c\langle x,y\rangle$
• $\langle x,cy\rangle=c\langle x,y\rangle$

이 성질들은 정의 4, 정의 9를 위의 식들에 대입하면 바로 증명될 수 있습니다.

위와 같이 정의한 내적을 이용해 복소벡터의 수직(orthogonality)의 개념도 정의할 수 있습니다.

정의 10
(a) 두 복소 벡터 $x$, $y$에 대하여 $$x^Hy=0$$ 이면 두 벡터가 서로 수직(orthogonal)이라고 말하고, $x\perp y$ 라고 씁니다.
(b) $n$개의 복소 벡터 $x_1$, $x_2$, $\cdots$, $x_n$에 대하여 $$x_i\,^Hx_j=0\quad(i\neq j)$$ 이면 이 벡터들이 pairwisely orthogonal하다고 말합니다.
(c) $n$개의 복소 벡터 $x_1$, $x_2$, $\cdots$, $x_n$에 대하여 $$x_i\,^Hx_j= \begin{cases} 0\quad(i\neq j)\\ 1\quad(i=j) \end{cases} $$ 이면 이 벡터들이 orthonormal하다고 말합니다.

즉,

\[u_1=\begin{bmatrix}1+2i\\2-i\end{bmatrix},\quad u_2=\begin{bmatrix}3\\1-i\end{bmatrix}\]

는 orthogonal 하지도, orthonormal하지도 않습니다. 반면,

\[v_1=\begin{bmatrix}3-i\\i\end{bmatrix},\quad v_2=\begin{bmatrix}1-i\\-2-4i\end{bmatrix}\]

는 orthogonal 하지만, orthonormal하지는 않습니다;

\[\begin{align*} v_1\,^Hv_1&=\sqrt{11} &v_1\,^Hv_2&=0\\ v_2\,^Hv_1&=0 &v_2\,^Hv_2&=\sqrt{22} \end{align*}\]

입니다. 따라서 두 열벡터 $v_1$과 $v_2$를 좌우로 나열하여 행렬

\[V=\begin{bmatrix}|&|\\v_1&v_2\\|&|\end{bmatrix}\]

를 만들면

\[V^HV=\begin{bmatrix}\sqrt{11}&0\\0&\sqrt{22}\end{bmatrix}\]

가 성립합니다.

이번에는 $v_1$, $v_2$를 조금 변형하여

\[w_1=\begin{bmatrix}\frac3{\sqrt{11}}-\frac1{\sqrt{11}}i\\\frac1{\sqrt{11}}i\end{bmatrix},\quad w_2=\begin{bmatrix}\frac1{\sqrt{22}}-\frac1{\sqrt{22}}i\\-\frac2{\sqrt{22}}-\frac4{\sqrt{22}}i\end{bmatrix}\]

를 만들면, $w_1$, $w_2$는 orthonormal하고

\[\begin{align*} w_1\,^Hw_1&=1 &w_1\,^Hw_2&=0\\ w_2\,^Hw_1&=0 &w_2\,^Hw_2&=1 \end{align*}\]

입니다. 행렬 $W$를

\[W=\begin{bmatrix}|&|\\w_1&w_2\\|&|\end{bmatrix}\]

로 두면

\[W^HW=I\]

가 성립합니다.

이때 $W$와 같은 행렬을 unitary 행렬이라고 부릅니다.

정의 11
복소수를 성분으로 가지는 정사각행렬 $A$가 $$A^HA=I$$ 를 만족시키면 $A$를 unitary 행렬(unitary matrix, 유니터리 행렬)이라고 부릅니다.

행렬의 orthogonality에 대하여 성질 12가 성립하는 것과 마찬가지로, unitarity에 대해서는 아래의 성질들이 성립합니다.

성질 12
(a) $n$차원의 orthonormal한 복소 벡터들 $n$개를 가로로 나열해서 얻은 행렬은 unitary 합니다.
(b) $A$가 unitary 행렬이면 $A$의 각 열들은 orthonormal 합니다.
(c) $A$가 unitary 행렬이면, $A$의 역행렬은 $A$의 conjugate transpose와 같습니다 ; $$A^{-1}=A^H$$

참고
(a) $A^TA=I$를 만족시키는 실수 행렬을 orthogonal 행렬이라고 했었습니다. 그리고 $A^HA=I$를 만족시키는 복소 행렬을 unitary 행렬이라고 했습니다. 따라서, 모든 orthogonal 행렬은 unitary 행렬이기도 합니다. $A$가 orthogonal 행렬이면, $A$의 모든 성분들은 실수이고 $A^TA=I$입니다. 그러면, 성질 3(a)에 의해 $$A^HA=A^TA=I$$ 이기 때문입니다.
(b) 두 벡터에 대한 orthogonality, 여러 벡터에 대한 pairwise orthogonality와 orthonormality에 대해서, 서로 다른 두 개의 정의를 내렸습니다(정의 06, 정의 10). 하지만 두 정의가 서로 상충되지는 않습니다. 만약 $x_i$가 실수벡터이면, 정의 10의 모든 식들은 정의 06의 식들과 일치하기 때문입니다.

1.5 행렬식

행렬의 대각화 개념은 eigenvalue/eigenvector와 관련되어 있는 개념입니다. 그런데 eigenvalue를 계산할 때, 많은 경우에 행렬식(determinant)이 사용되므로 이에 대해 먼저 이야기했습니다. 하지만, 행렬식에 대해 말하려면 복잡하면서도 기본적인 설명들이 많이 들어갈 수밖에 없습니다. 특히, 선형대수의 모든 개념들을 다 설명하면서 글을 쓰고 있지 않으므로, 이 포스트에서는 행렬식에 관한 설명ㅣ 꽤 복잡하게 쓰였습니다.

이번 절 1.5 행렬식의 내용이 너무 복잡하면, $2\times 2$ 행렬과 $3\times3$ 행렬의 행렬식의 정의와 정리 14 정도만 인정하고 넘어가도 이 포스트의 뒷부분을 이해하는 데에는 문제가 없을 것 같습니다.

고등학교 수학에서 행렬식의 개념에 대해 다룹니다. 행렬

\[A=\begin{bmatrix}a&b\\c&d\end{bmatrix}\]

의 행렬식은 $D=ad-bc$이고, $D$가 0이면 역행렬이 존재하지 않고, 0이 아니면 역행렬이 존재한다는 것입니다. 이 포스트에서는 $A$의 행렬식을 $\text{det}(A)$로 적으려 합니다. 따라서, 행렬

\[A=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}\]

에 대한 행렬식은

\[\text{det}A = a_{11}a_{22}-a_{12}a_{21}\]

이 됩니다. 또한, 흔히 대학 1학년 수준의 미적분학에 보면 $3\times3$ 행렬

\[A=\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{bmatrix}\]

에 대한 행렬식이

\[\begin{multline*} \text{det}A = a_{11}a_{22}a_{33}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33} +a_{12}a_{23}a_{31}-a_{13}a_{21}a_{32}+a_{13}a_{22}a_{31} \end{multline*}\]

라는 것을 다루기도 합니다.

일반적인 행렬식에 대해 정의하려면 먼저 permutation(순열)에 대해 말해야합니다. 여기서 말하는 순열은 고등학교 수학에서 다루는 $_5P_3=5\times4\times3=60$와 는 조금 다릅니다.

permutation

중학교 수학(혹은 고등학교 수학)에서 함수란 두 집합 $X$, $Y$가 주어졌을 때

$X$의 모든 원소 $x\in X$에 대하여 $Y$의 한 원소 $f(x)$에 대응시키는 것

을 말합니다. 이때, $X$를 정의역(domain), $Y$를 공역(codomain)이라고 부릅니다. 예를 들어, 두 집합 $X=\{a,b,c\}$, $Y=\{1,2,3\}$에 대하여 $a$를 $1$로 대응시키고, $b$를 $3$으로 대응시키고 $c$도 3으로 대응시키는 함수를 $f$라고 하면,

\[\begin{align*} f(a)&=1\\ f(b)&=3\\ f(c)&=3 \end{align*}\]

로 표현할 수 있고, 아래의 (1)번 그림으로도 나타낼 수 있습니다.

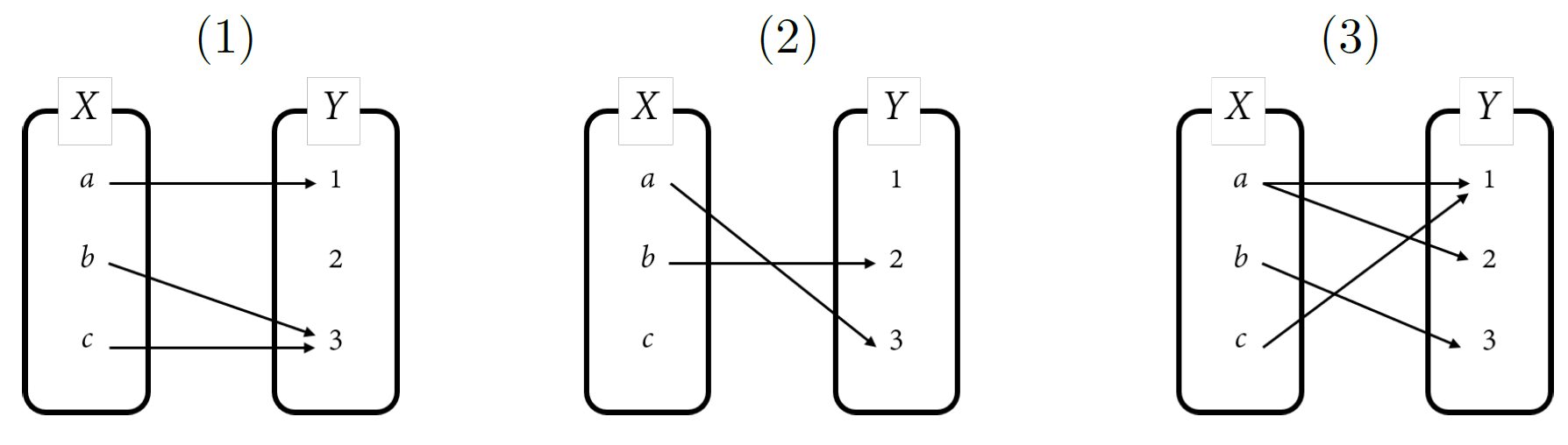
이 그림의 (2)번은 $a$가 3으로 대응되고 $b$가 2로 대응되었으나, $c$는 어디에도 대응되지 않았기 때문에 함수라고 할 수 없습니다. (3)번 또한, $a$가 서로 다른 두 개의 $Y$의 원소 1, 2에 대응되었으므로 이것도 함수라고 할 수 없습니다.

함수 중에서

$x_1\ne x_2$이면 $f(x_1)\ne f(x_2)$이다.

를 만족시키키는 함수를 일대일함수(one-to-one function, injection, 단사함수)라고 합니다. 또한, 일대일함수 중에서

모든 $y\in Y$에 대하여 $y=f(x)$를 만족시키는 $x$가 적어도 하나 존재한다.

라는 조건을 만족시키는 함수를 일대일대응(one-to-one correspondence, bijection, 전단사함수)이라고 합니다.

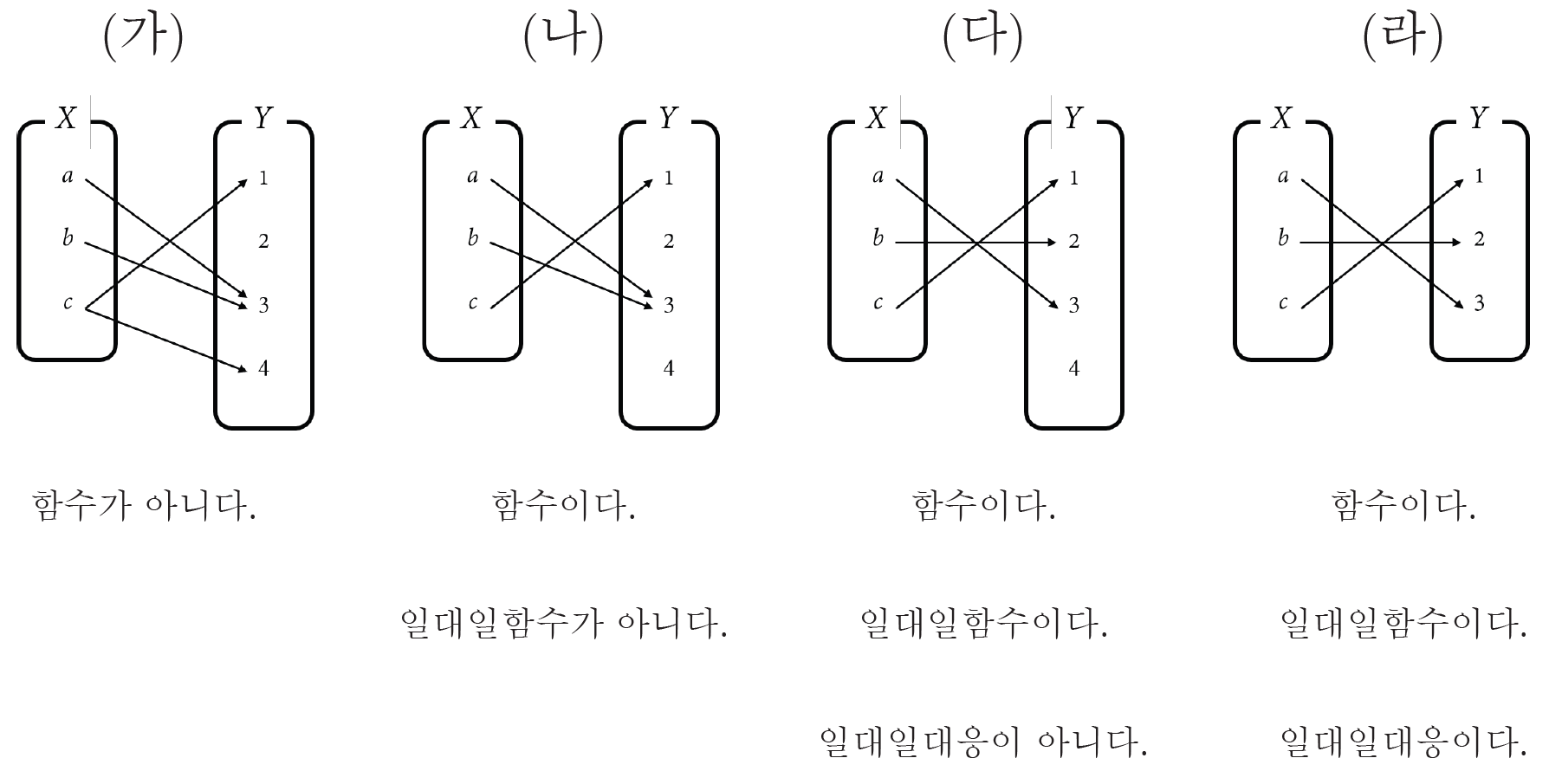
예를 들어, 아래 그림에서 (가)는 함수라고 할 수 없고 (나), (다), (라)는 함수라고 할 수 있는데, 그중 (나)는 $a\ne b$인데도 불구하고 $f(a)=f(b)$이므로 일대일함수가 아닙니다. 하지만 (다), (라)는 일대일함수 조건을 만족하므로 일대일함수입니다. (다), (라) 중에서는 (라)가 일대일대응 조건을 만족시킵니다. $1\in Y$은 $f(c)=1$을 만족시키는 $c\in X$가 존재하고, $2\in Y$은 $f(b)=2$을 만족시키는 $b\in X$가 존재하며, $3\in Y$은 $f(a)=3$을 만족시키는 $a\in X$가 존재하기 때문입니다. 그런데 (다)의 경우에는 $4\in Y$가 $f(x)=4$를 만족시키는 $x\in X$가 존재하지 않기 때문에 일대일대응이 아닙니다.

이제 permutation(순열)을 정의할 수 있습니다. $n$이 자연수일 때, 정의역과 공역이 모두 $\mathbb N_n=\{1,2,\cdots,n\}$인 일대일대응을 permutation이라고 합니다.

예를 들어 $n=3$인 permutation들은 아래와 같습니다.

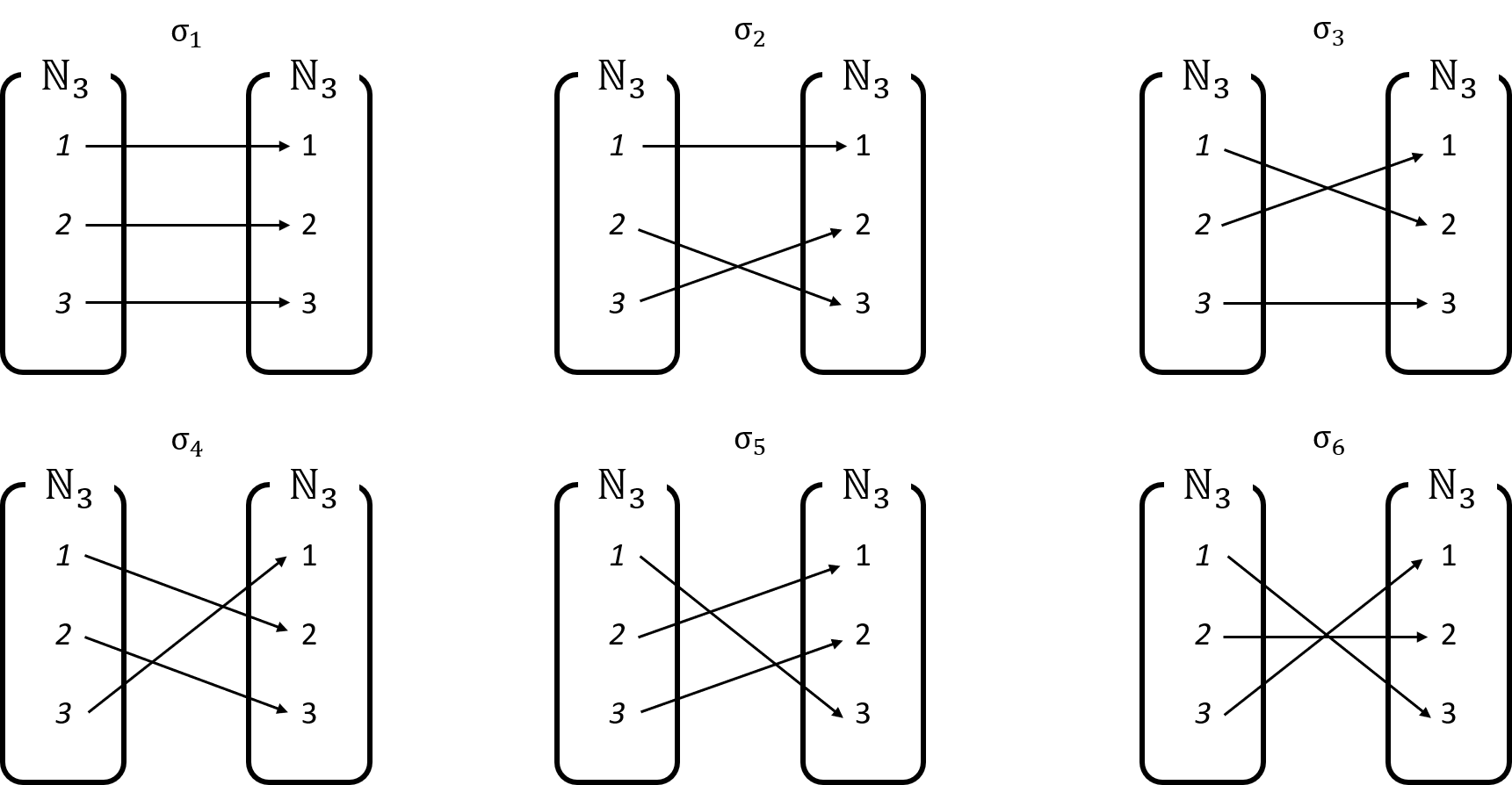
일반적으로 $n$의 permutation의 개수는 $n!$ 개일 것입니다. 따라서, $n=3$인 permutation들의 개수는 $3!=6$ 개이므로, 위의 그림은 모든 permutation들을 다 나타낸 셈입니다.

$n$의 permutation들의 집합을 $S_n$이라고 표기하겠습니다. 이 집합은 symmetric group(대칭군)이라는 이름을 가지고 있습니다. 유한집합 $X$의 원소의 개수를 $|X|$로 표현한다고 하면, $|S_3|=6$로 쓸 수 있습니다.

$\sigma$가 permutation일 때, $\sigma$를 표현하는 방법은 다양하지만, 그 중 가장 간단한 방법은 $\sigma(1)$, $\sigma(2)$, $\cdots$, $\sigma(3)$를 단순히 나열하는 것입니다. 예를 들어 위 그림의 첫번째 permutation인 $\sigma_1$은

\[\begin{cases} \sigma_1(1)=1\\ \sigma_1(2)=2\\ \sigma_1(3)=3 \end{cases}\]

을 만족시키므로 \(\sigma_1=123\)으로 나타내는 것입니다. 두번째 permutation인 $\sigma_2$는

\[\begin{cases} \sigma_2(1)=1\\ \sigma_2(2)=3\\ \sigma_2(3)=2 \end{cases}\]

이므로, $\sigma_2=132$라고 간략히 씁니다. 이러한 표기법으로 여섯 개의 permutation $\sigma_i$를 모두 표현하면

\[\begin{align*} &\sigma_1=123,\quad&&\sigma_2=132,\quad&&\sigma_3=213, \\ &\sigma_4=231,\quad&&\sigma_5=312,\quad&&\sigma_6=321 \end{align*}\]

이 됩니다.

이번에는 각각의 permutation들을 even permutation과 odd permutation으로 나누고, permutation $\sigma$의 부호 $\text{sgn}(\sigma)$를 정의하려 합니다. 어떤 permutation $\sigma=abc$에 대하여 $a$, $b$, $c$를 이 permutation의 ‘성분’라고 할 때, $\sigma$의 서로 다른 두 성분를 바꾸는 것을 ‘교환’이라고 하겠습니다. 예를 들어 $\sigma=abc$의 첫번째와 두번째 성분을 교환하면 $bac$가 됩니다. $\sigma=abc$의 두번째 성분과 세번째 성분을 교환하면 $acb$가 됩니다. 이때,

• $\sigma$를 짝수번 교환하여 항등함수를 만들 수 있으면 $\sigma$를 even permutation이라고 합니다.
• $\sigma$를 홀수번 교환하여 항등함수를 만들 수 있으면 $\sigma$를 odd permutation이라고 합니다.
• 함수 $\text{sgn}:S_n\to\{1,-1\}$을 다음과 같이 정의합니다;

\[\text{sgn}(\sigma)= \begin{cases} 1&(\sigma : \text{even})\\ -1&(\sigma : \text{odd}) \end{cases}\]

여기에서 항등함수란, 모든 $x$에 대하여 $f(x)=x$인 함수 $f$를 말합니다. 따라서, $S_3$에서는 $\sigma_1=123$이 항등함수입니다.

예를 들어, $\sigma_1=123$의 경우에는 그 자체로 항등함수이므로 0번 교환하여 항등함수를 만들 수 있고, $0$은 짝수이므로 $\sigma_1$은 even permutation입니다. 따라서, $\text{sgn}(\sigma_1)=1$입니다.

$\sigma_2=132$의 경우에는 $132$의 $3$과 $2$를 교환하면 항등함수 $123$를 만들 수 있습니다. $1$번 교환하여 항등함수를 만들었고, $1$은 홀수이므로 $\sigma_2$는 odd permutation이며 $\text{sgn}(\sigma_2)=-1$입니다. 사실, $\sigma_2=132$는 $1$과 $3$을 교환하여여 $312$를 만들고, 다시 3과 1을 교환하여 $132$로 돌아온 뒤, $3$ $2$를 교환하여 $123$를 만들 수 있습니다. 이 경우에는 $\sigma_2=132$의 성분을 3번 교환했는데, 그럼에도 불구하고 $\sigma_2$가 odd permutation이라는 사실은 변하지 않습니다.

$\sigma_4=231$의 경우에는 짝수번 교환해야 항등함수 $\sigma_1=123$이 됩니다. 예를 들어 $\sigma_4=231$의 $3$과 $1$을 교환하여 $\sigma_2=213$를 얻고, 다시 $2$와 $1$을 교환하여 $\sigma_1=123$을 얻을 수 있기 때문입니다.

$n=3$인 6개의 permutation에 대해서 부호를 계산하면 다음과 같습니다.

\[\begin{align*} \text{sgn}(\sigma_1)&=1 &\text{sgn}(\sigma_2)&=-1 &\text{sgn}(\sigma_3)&=-1 \\ \text{sgn}(\sigma_4)&=1 &\text{sgn}(\sigma_5)&=1 &\text{sgn}(\sigma_3)&=-1 \end{align*}\]

즉, $n=3$인 permutation은 총 6개가 있는데, 그 중 even permutation은 3개, odd permutation은 3개가 있습니다.

참고
(a) 자연수 $n$에 대하여, 모든 permutation들의 집합을 $S_n$이라고 쓰고, 이 집합을 permutation group(대칭군)이라고 부른다고 했었습니다. 모든 even permutation들의 집합은 $A_n$이라고 쓰고, 이 집합을 alternating group(교대군)이라고 부릅니다. 모든 odd permutation들의 집합은 $S_n-A_n$이 되지만, 이것은 군(group)을 이루지는 않습니다.
일반적으로, even permutation의 개수와 odd permutation의 개수는 같습니다. 따라서 $n$에 대한 even permutation들의 개수는 $\frac{n!}2$이고, odd permutation들의 개수도 $\frac{n!}2$입니다.
이에 대한 증명은 꽤 쉽습니다. odd permutation 중 하나를 골라서 $\beta$라고 하겠습니다. 임의의 even permutation $\alpha\in A_n$에 대하여 $g(\alpha)$를
$$g(\alpha)=\beta\circ\alpha$$
로 적습니다. 그러면 $g(\alpha)$는 odd permutation이 되고, 따라서 $g$는 $A_n$에서 $S_n-A_n$으로 가는 함수가 됩니다. 더구나 이 함수 $g$는 일대일대응 조건까지도 만족시킵니다. 따라서 $g$의 정의역인 $A_n$과 $g$의 공역인 $S_n-A_n$은 그 개수가 같습니다.
(b) $\alpha\in S_n$에 대하여 $\sigma\mapsto\sigma\circ\alpha$는 일대일대응입니다. 다시 말해, $F(\sigma)=\sigma\circ\alpha$로 정의된 함수 $F:S_n\to S_n$은 일대일대응 조건을 만족시킵니다. 왜냐하면 $F(\sigma_1)=F(\sigma_2)$이면 $\sigma_1\circ\alpha=\sigma_2\circ\alpha$이고, 양변의 오른쪽에 $\alpha^{-1}$을 합성해주면 $\sigma_1=\sigma_2$가 되기 때문에 $F$가 일대일함수이고, 임의의 $\beta\in S_n$에 대하여 $F(\sigma^{-1}\circ\beta)=\sigma\circ(\sigma^{-1}\circ\beta)=(\sigma\circ\sigma^{-1})\circ\beta=\beta$인 $\sigma^{-1}\circ\beta\in S_n$이 존재하므로 $F$는 일대일대응이기 때문입니다.
또, $\sigma\mapsto\circ\sigma^{-1}$는 일대일대응입니다. 다시 말해, $G(\sigma)=\sigma^{-1}$로 정의된 함수 $G:S_n\to S_n$은 일대일대응 조건을 만족시킵니다. 왜냐하면 $G(\sigma_1)=G(\sigma_2)$이면 ${\sigma_1}^{-1}={\sigma_2}^{-1}$이고, $\sigma_2=\sigma_2\circ{\sigma_1}^{-1}\circ\sigma_1=\sigma_2\circ{\sigma_2}^{-1}\circ\sigma_1=\sigma$ 이므로 $G$가 일대일함수이고, 임의의 $\beta\in S_n$에 대하여 $G(\beta^{-1}=(\beta^{-1})^{-1}=\beta$인 $\beta^{-1}\in S_n$이 존재하므로 $G$는 일대일대응이기 때문입니다.
이 두 함수 $F$, $G$와 그 합성이 일대일대응이라는 사실은 정리 14(a)를 증명하는 데에 사용됩니다.
(c) permutation의 부호함수 $\text{sgn}$에 대하여 다음과 같은 사실들이 성립합니다. ($\alpha,\beta\in S_n$) (증명은 생략합니다.)

• 함수 $\text{sgn}:S_n\to\{1,-1\}$은 잘 정의된 함수입니다.
• $\text{sgn}(\alpha\circ\beta)=\text{sgn}(\alpha)\text{sgn}(\beta)$
• $\text{sgn}(\alpha\circ\alpha)=1$
• $\text{sgn}(\alpha^{-1})=\text{sgn}(\alpha)$

한편, $n=2$이면 permutation의 개수는 $2!=2$개입니다. $S_2=\{\sigma_1,\sigma_2\}$라고 하면,

\[\begin{align*} \sigma_1&=12,\quad&\text{sgn}(\sigma_1)&=1\\ \sigma_2&=21,\quad&\text{sgn}(\sigma_2)&=-1 \end{align*}\]

입니다.

행렬식

이제 행렬식을 정의할 수 있습니다.

정의 13
$n\times n$ 정사각행렬 $A$에 대하여 행렬식 $\text{det}(A)$를 $$\text{det}(A)=\sum_{\sigma\in S_n}\left(\text{sgn}(\sigma)\prod_{i=1}^na_{i,\sigma(i)}\right)$$ 로 정의합니다. 행렬식은 $|A|$와 같이 표기하기도 합니다.

여기에서 $\prod$는 곱의 기호입니다. 이것은 합의 기호 $\sum$과 비슷하게 쓰입니다. 예를 들어 1, 2, $\cdots$, $n$을 차례로 더하는 것을

\[\sum_{k=1}^nk=1+2+\cdots+n=\frac{n(n+1)}2\]

와 같이 표현하듯이, 차례로 곱하는 것은

\[\prod_{k=1}^nk=1\times2\times\cdots\times n=n!\]

과 같이 표현됩니다. 더 예를 들면 다음과 같습니다. 등차수열 $a_k=2k$를 차례로 더하거나 곱하면

\[\begin{align*} \sum_{k=1}^n2k&=2\sum_{k=1}^nk=n(n+1)\\ \prod_{k=1}^n2k&=\left(\prod_{k=1}^n2\right)\left(\prod_{k=1}^nk\right)=2^n\times n! \end{align*}\]

이 되고, 등비수열 $b_k=2^k$를 차례로 더하거나 곱하면

\[\begin{align*} \sum_{k=1}^n2^k&=\frac{2(2^n-1)}{2-1}=2(2^n-1)\\ \prod_{k=1}^n2^k&=2^{1+2+\cdots+n}=2^{\frac{n(n+1)}2} \end{align*}\]

가 됩니다.

정의 13의 식은 복잡해보이지만, 잘 풀어보면 위에서 알아본 $2\times2$ 행렬에서의

\[\text{det}A = a_{11}a_{22}-a_{12}a_{21}\]

와 $3\times3$ 행렬에서의

\[\text{det}A = a_{11}a_{22}a_{33}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}+a_{12}a_{23}a_{31}-a_{13}a_{21}a_{32}+a_{13}a_{22}a_{31}\]

에 대응되는 식임을 확인할 수 있습니다.

$2\times2$ 행렬의 경우를 먼저 보면, $(S_2=\{\sigma_1,\sigma_2\})$

\[\begin{align*} \sigma_1&=12,\quad&\text{sgn}(\sigma_1)&=1\\ \sigma_2&=21,\quad&\text{sgn}(\sigma_2)&=-1 \end{align*}\]

였으므로

\[\begin{align*} \text{det}(A) &=\sum_{\sigma\in S_2}\left(\text{sgn}(\sigma)\prod_{i=1}^2a_{i,\sigma(i)}\right)\\ &=\text{sgn}(\sigma_1)\prod_{i=1}^2a_{i,\sigma_1(i)} +\text{sgn}(\sigma_2)\prod_{i=1}^2a_{i,\sigma_2(i)}\\ &=a_{1,\sigma_1(1)}a_{2,\sigma_1(2)}-a_{1,\sigma_2(1)}a_{2,\sigma_2(2)}\\ &=a_{11}a_{22}-a_{12}a_{21} \end{align*}\]

인 것입니다.

$3\times3$ 행렬의 경우에도 ($S_3=\{\sigma_1,\sigma_2,\cdots,\sigma_6\}$)

\[\begin{align*} \sigma_1&=123,\quad&\text{sgn}(\sigma_1)&=1\\ \sigma_2&=132,\quad&\text{sgn}(\sigma_1)&=-1\\ \sigma_3&=213,\quad&\text{sgn}(\sigma_1)&=-1\\ \sigma_4&=231,\quad&\text{sgn}(\sigma_1)&=1\\ \sigma_5&=312,\quad&\text{sgn}(\sigma_1)&=1\\ \sigma_6&=321,\quad&\text{sgn}(\sigma_1)&=-1\\ \end{align*}\]

이었기 때문에

\[\begin{align*} \text{det}(A) =&\sum_{\sigma\in S_3}\left(\text{sgn}(\sigma)\prod_{i=1}^3a_{i,\sigma(i)}\right)\\ =&\text{sgn}(\sigma_1)\prod_{i=1}^3a_{i,\sigma_1(i)} +\text{sgn}(\sigma_2)\prod_{i=1}^3a_{i,\sigma_2(i)} +\text{sgn}(\sigma_3)\prod_{i=1}^3a_{i,\sigma_3(i)}\\ &+\text{sgn}(\sigma_4)\prod_{i=1}^3a_{i,\sigma_4(i)} +\text{sgn}(\sigma_5)\prod_{i=1}^3a_{i,\sigma_5(i)} +\text{sgn}(\sigma_6)\prod_{i=1}^3a_{i,\sigma_6(i)}\\ =&a_{1,\sigma_1(1)}a_{2,\sigma_1(2)}a_{3,\sigma_1(3)} -a_{1,\sigma_2(1)}a_{2,\sigma_2(2)}a_{3,\sigma_2(3)} -a_{1,\sigma_3(1)}a_{2,\sigma_3(2)}a_{3,\sigma_3(3)}\\ &+a_{1,\sigma_4(1)}a_{2,\sigma_4(2)}a_{3,\sigma_4(3)} +a_{1,\sigma_5(1)}a_{2,\sigma_5(2)}a_{3,\sigma_5(3)} -a_{1,\sigma_6(1)}a_{2,\sigma_6(2)}a_{3,\sigma_6(3)}\\ =&a_{11}a_{22}a_{33} -a_{11}a_{23}a_{32} -a_{12}a_{21}a_{33} +a_{12}a_{23}a_{31} +a_{13}a_{21}a_{32} -a_{13}a_{22}a_{31} \end{align*}\]

이 됩니다.

행렬식에 대하여 앞으로 사용될 사실은 다음의 두 명제입니다.

정리 14
(a) 정사각행렬 $A$, $B$에 대하여 $$\text{det}(AB)=\text{det}(A)\text{det}(B)$$ 입니다.
(b) 정사각행렬 $A$에 대하여 $A$의 역행렬이 존재하기 위한 필요충분조건은 $\text{det}(A)\neq0$인 것입니다.

증명 : 정리 14(a)

아래 증명은 이 증명에서 오타로 보이는 것을 수정하고, 설명을 덧붙인 것입니다. 선형대수의 다른 개념들을 사용하지 않고 계산만을 이용해 증명하려다보니, 증명과정이 조금 복잡합니다.

\[\begin{align*} \text{det}(AB) &=\sum_{\sigma\in S_n}\text{sgn}(\sigma)\prod_{k=1}^n(AB)_{k,\sigma(k)}\\ &=\sum_{\sigma\in S_n}\text{sgn}(\sigma)\prod_{k=1}^n\left(\sum_{i=1}^nA_{ki}B_{i,\sigma(k)}\right)\\ &=\sum_{\sigma\in S_n}\text{sgn}(\sigma)\left(\sum_{f:\mathbb N_n\to\mathbb N_n}\prod_{k=1}^nA_{k,f(k)}B_{f(k),\sigma(k)}\right)\\ &=\sum_{\sigma\in S_n}\sum_{f:\mathbb N_n\to\mathbb N_n}\text{sgn}(\sigma)\prod_{k=1}^nA_{k,f(k)}B_{f(k),\sigma(k)}\\ &=\sum_{f:\mathbb N_n\to\mathbb N_n}\sum_{\sigma\in S_n}\text{sgn}(\sigma)\prod_{k=1}^nA_{k,f(k)}B_{f(k),\sigma(k)}\\ &=\sum_{f:\mathbb N_n\to\mathbb N_n}\sum_{\sigma\in S_n}\text{sgn}(\sigma)\left(\prod_{k=1}^nA_{k,f(k)}\right)\left(\prod_{k=1}^nB_{f(k),\sigma(k)}\right)\\ =&\sum_{f:\mathbb N_n\to\mathbb N_n}\left(\prod_{k=1}^nA_{k,f(k)}\right)\left(\sum_{\sigma\in S_n}\text{sgn}(\sigma)\prod_{k=1}^nB_{f(k),\sigma(k)}\right) \end{align*}\]

위의 계산에서 두번째 줄은 행렬의 곱 $AB$의 성분에 대한 정의를 쓴 것입니다. 세번째 줄에 대한 설명은 다음과 같습니다.

보통 중학교 과정에 있는 내용이지만, $(a_1+a_2)(b_1+b_2)$를 전개한다는 것은

\[(a_1+a_2)(b_1+b_2)=a_1b_1+a_1b_2+a_2b_1+a_2b_2\]

와 같이 쓰는 것입니다. 이것은

$a_1$와 $a_2$ 중에서 하나를 고르고 $b_1$와 $b_2$ 중에서 하나를 골라서 곱한 뒤 가능한 모든 조합을 더하는 것

을 말합니다. 이것을 조금 형식적으로 쓰면,

$f:\{1,2\}\to\{1,2\}$인 함수 하나를 고르고, 가능한 모든 $a_{f(1)}b_{f(2)}$의 조합을 더하는 것

과 정확히 일치합니다. $f:\{1,2\}\to\{1,2\}$인 함수는 다음의 네 개 함수입니다.

\[\begin{cases} f_1(1)=1\\f_1(2)=1 \end{cases},\qquad \begin{cases} f_2(1)=1\\f_2(2)=2 \end{cases},\qquad \begin{cases} f_3(1)=2\\f_3(2)=1 \end{cases},\qquad \begin{cases} f_4(1)=2\\f_4(2)=2 \end{cases}.\]

따라서, 가능한 모든 $a_{f(1)}b_{f(2)}$의 조합은

\[a_{f_1(1)}b_{f_1(2)}=a_1b_1,\quad\\ a_{f_2(1)}b_{f_2(2)}=a_1b_2,\quad\\ a_{f_3(1)}b_{f_3(2)}=a_2b_1,\quad\\ a_{f_4(1)}b_{f_4(2)}=a_2b_2,\quad\]

이라서 이것들을 모두 더하면 $a_1b_1+a_1b_2+a_2b_1+a_2b_2$이 되는 것입니다. $a_i=c_{1i}$, $b_i=c_{2i}$로 적고, 위의 전개과정을 다시 쓰면

\[\prod_{k=1}^2\left(\sum_{i=1}^2c_{ki}\right)=\sum_{f:\{1,2\}\to\{1,2\}}\prod_{k=1}^nc_{k,f(k)}\]

로 쓸 수 있는 것입니다. 따라서 원래 계산의 두번째 줄의

\[\prod_{k=1}^n\left(\sum_{i=1}^nA_{ki}B_{i,\sigma(k)}\right)\]

을

\[\sum_{f:\mathbb N_n\to\mathbb N_n}\prod_{k=1}^nA_{k,f(k)}B_{f(k),\sigma(k)}\]

로 쓸 수 있는 것입니다.

이후 네번째 줄부터 마지막까지는 합의 기호$\left(\sum\right)$의 순서를 바꾸거나 상수를 빼거나 넣은 것에 해당합니다. 마지막 식에서, 함수 $f:\mathbb N_n\to\mathbb N_n$는 일대일대응인 것 $(f\in S_n)$과 그렇지 않은 것 $(f\not\in S_n)$ 으로 나눌 수 있습니다.

따라서

\[\begin{align*} \text{det}(AB)&=P+Q\\ P&=\sum_{f\in S_n}\left(\prod_{k=1}^nA_{k,f(k)}\right)\left(\sum_{\sigma\in S_n}\text{sgn}(\sigma)\prod_{k=1}^nB_{f(k),\sigma(k)}\right)\\ Q&=\sum_{f:\not\in S_n}\left(\prod_{k=1}^nA_{k,f(k)}\right)\left(\sum_{\sigma\in S_n}\text{sgn}(\sigma)\prod_{k=1}^nB_{f(k),\sigma(k)}\right) \end{align*}\]

로 쓸 수 있습니다. $Q$를 먼저 계산합시다. $f$가 일대일대응이 아니면 이것은 일대일함수가 아닙니다. (항상 그런 것은 아니지만, 이 경우에는 정의역과 공역이 같기 때문에 그렇습니다.) 따라서 $f(k_1)=f(k_2)$인 $k_1\ne k_2$가 존재합니다. 만약, $k_1$과 $k_2$를 바꾸는 교환을 $\alpha$라고 하면

\[\begin{align*} \prod_{k=1}^nB_{f(k),(\sigma\circ\alpha)(k)} &=B_{f(1),(\sigma\circ\alpha)(1)}\times\cdots\times B_{f(k_1),(\sigma\circ\alpha)(k_1)} \times\cdots\times B_{f(k_2),(\sigma\circ\alpha)(k_2)}\times\cdots\times B_{f(n),(\sigma\circ\alpha)(n)}\\ &=B_{f(1),\sigma(1)}\times\cdots\times B_{f(k_1),\sigma(k_2)} \times\cdots\times B_{f(k_2),\sigma(k_1)}\times\cdots\times B_{f(n),\sigma(n)}\\ &=B_{f(1),\sigma(1)}\times\cdots\times B_{f(k_2),\sigma(k_2)} \times\cdots\times B_{f(k_1),\sigma(k_1)}\times\cdots\times B_{f(n),\sigma(n)}\\ &=\prod_{k=1}^nB_{f(k),\sigma(k)} \end{align*}\]

이고, $\text{sgn}(\alpha\circ\sigma)=\text{sgn}(\alpha)\text{sgn}(\sigma)=-\text{sgn}(\sigma)$ 이므로, 위의 $Q$ 식에서 두번째 괄호의 두 배는 0이 됩니다;

\[\begin{align*} &2\sum_{\sigma\in S_n}\text{sgn}(\sigma)\prod_{k=1}^nB_{f(k),\sigma(k)}\\ =&\sum_{\sigma\in S_n}\text{sgn}(\sigma)\prod_{k=1}^nB_{f(k),\sigma(k)} +\sum_{\sigma\in S_n}\text{sgn}(\sigma)\prod_{k=1}^nB_{f(k),\sigma(k)}\\ =&\sum_{\sigma\in S_n}\text{sgn}(\sigma)\prod_{k=1}^nB_{f(k),\sigma(k)} +\sum_{\sigma\in S_n}\text{sgn}(\sigma\circ\alpha)\prod_{k=1}^nB_{f(k),(\sigma\circ\alpha)(k)}\\ =&\sum_{\sigma\in S_n}\text{sgn}(\sigma)\prod_{k=1}^nB_{f(k),\sigma(k)} +\sum_{\sigma\in S_n}\left(-\text{sgn}(\sigma)\right)\prod_{k=1}^nB_{f(k),\sigma(k)}\\ =&0 \end{align*}\]

세번째 줄에서 $\sum_{\sigma\in S_n}$의 항에 $\sigma$ 대신 $\sigma\circ\alpha$를 넣었고, 그 전후의 결과는 같습니다. 왜냐하면 1.5의 첫번째 참고(b)에서 $\sigma\mapsto\sigma\circ\alpha$는 일대일대응이라고 했었기 때문입니다. 이러한 방식의 논증은 이후 계산들에서도 두어번 나타납니다.

결국, $Q=0$입니다. 한편, $P$를 계산하면

\[\begin{align*} P &=\sum_{f\in S_n}\left(\prod_{k=1}^nA_{k,f(k)}\right)\left(\sum_{\sigma\in S_n}\text{sgn}(\sigma)\prod_{k=1}^nB_{f(k),\sigma(k)}\right)\\ &=\sum_{f\in S_n}\left(\prod_{k=1}^nA_{k,f(k)}\right)\left(\sum_{\sigma\in S_n}\text{sgn}(\sigma)\prod_{k=1}^nB_{(f\circ\sigma^{-1})(k),k}\right)\\ &=\sum_{f\in S_n}\left(\prod_{k=1}^nA_{k,f(k)}\right)\left(\sum_{\sigma\in S_n}\text{sgn}(\sigma^{-1})\prod_{k=1}^nB_{(f\circ\sigma^{-1})(k),k}\right)\\ &=\sum_{f\in S_n}\left(\prod_{k=1}^nA_{k,f(k)}\right)\left(\sum_{\sigma\in S_n}\text{sgn}(f\circ\sigma^{-1})\cdot\text{sgn}(f)\prod_{k=1}^nB_{(f\circ\sigma^{-1})(k),k}\right)\\ &=\sum_{f\in S_n}\left(\prod_{k=1}^nA_{k,f(k)}\right)\left(\sum_{\pi\in S_n}\text{sgn}(\pi)\cdot\text{sgn}(f)\prod_{k=1}^nB_{\pi(k),k}\right)\\ &=\sum_{f\in S_n}\text{sgn}(f)\left(\prod_{k=1}^nA_{k,f(k)}\right)\left(\sum_{\pi\in S_n}\text{sgn}(\pi)\prod_{k=1}^nB_{\pi(k),k}\right)\\ &=\left(\sum_{f\in S_n}\text{sgn}(f)\prod_{k=1}^nA_{k,f(k)}\right)\left(\sum_{\pi\in S_n}\text{sgn}(\pi)\prod_{k=1}^nB_{\pi(k),k}\right)\\ &=\text{det}(A)\text{det}(B^T)\\ &=\text{det}(A)\text{det}(B) \end{align*}\]

입니다. 두번째 줄에서 $\sigma^{-1}$이 일대일대응이므로 \(\prod_{k=1}^n\)에서 $k$ 대신 $\sigma^{-1}(k)$를 사용하여도 그 곱은 여전히 같습니다. 다섯번째 줄에서 $f\circ\sigma^{-1}$를 $\pi$로 치환하고, 합 또한 $\pi$에 대한 합으로 바꾸었는데, 이는 $\sigma\mapsto f\circ\sigma^{-1}$가 일대일대응이기 때문에 가능합니다. 마지막 부분에서 $\text{det}(B^T)=\text{det}(B)$인 것은

\[\begin{align*} \text{det}(B) &=\sum_{\sigma\in S_n}\text{sgn}(\sigma)\prod_{k=1}^nb_{k,\sigma(k)}\\ &=\sum_{\sigma\in S_n}\text{sgn}(\sigma^{-1})\prod_{k=1}^nb_{k,\sigma(k)}\\ &=\sum_{\sigma\in S_n}\text{sgn}(\sigma^{-1})\prod_{k=1}^nb_{\sigma^{-1}(k),k}\\ &=\sum_{\pi\in S_n}\text{sgn}(\pi)\prod_{k=1}^nb_{\pi(k),k}\\ &=\text{det}(B^T) \end{align*}\]

로 설명될 수 있습니다. 이때 세번째 줄에서는 $\sigma^{-1}$이 일대일대응이므로 \(\prod_{k=1}^n\)에서 $k$ 대신 $\sigma^{-1}(k)$를 사용했습니다. 네번째 줄에서는 $\sigma^{-1}$이 $\pi$로 치환되고 \(\sum_{\sigma\in S_n}\)이 \(\sum_{\pi\in S_n}\)로 바뀌었는데, 이것은 $\sigma\mapsto\sigma^{-1}$이 일대일대응이기 때문에 가능한 일입니다. 위의 결과를 요약하면

\[\text{det}(AB)=P+Q=\text{det}(A)\text{det}(B)+0=\text{det}(A)\text{det}(B)\]

가 됩니다. $\square$

정리 14(b)에 대한 증명은 다음과 같습니다.

증명 [ 정리 14(b)의 $\Rightarrow$ 방향 ] $A$의 역행렬이 존재하면 $\text{det}(A)\neq0$ 입니다.

만약 $A$의 역행렬이 존재하면 $AB=I$를 만족시키는 정사각행렬 $B$가 존재합니다. 그러면 (a)에 의해 \(\text{det}(A)\text{det}(B)=\text{det}(AB)=\text{det}(I)=1\) 입니다. 따라서 $\text{det}(A)=0$이 될 수 없습니다. $\square$

증명 [ 정리 14(b)의 $\Leftarrow$ 방향 ] $\text{det}(A)\neq0$이면, $A$의 역행렬이 존재합니다.

이 증명은 반대방향의 증명보다 조금 복잡하며, 이 포스트에 소개한 선형대수의 개념만 가지고는 증명할 수 없는 것처럼 보입니다. 소개하지 않은 개념들을 사용하여 증명할 때 가능한 증명방식 중 하나는, 원래 명제의 대우를 통해 증명하는 것으로 아래와 같습니다.

만약 $A$의 역행렬이 존재하지 않으면, $A$는 일대일함수가 아닙니다. 따라서 $Ax_1=Ax_2$인 $x_1\ne x_2$가 존재하고, 이는 곧 영벡터이 아니면서 $Ax=0$을 만족시키는 벡터 $x\in\mathbb R^n$이 존재한다는 뜻입니다($x=x_2-x_1$). 행렬 $A$의 $i$번째 열을 $A_i$로 표현하면, 이것은 $A_1$, $A_2$, $\cdots$, $A_n$이 linearly dependent하다는 것을 의미합니다. 따라서 $\text{det}(A)=0$입니다. $\square$

2 직교대각화

2.1 eigenvalue / eigenvector

이제 eigenvalue와 eigenvector에 대해 말할 수 있습니다.

정의 15
정사각행렬 $A$에 대하여 $$Ax=\lambda x$$ 를 만족시키는 복소수 $\lambda$와 벡터 $x(\ne0)$가 존재하면 $\lambda$를 eigenvalue(고윳값, 고유치), $x$를 eigenvector(고유벡터)라고 부릅니다.

예를 들어, 행렬

\[P=\begin{bmatrix}2&2\\0&1\end{bmatrix}\]

에 대해서

\[\begin{bmatrix}2&2\\0&1\end{bmatrix}\begin{bmatrix}1\\0\end{bmatrix} =\begin{bmatrix}2\\0\end{bmatrix}=2\begin{bmatrix}1\\0\end{bmatrix}\]

이므로

\[x=\begin{bmatrix}1\\0\end{bmatrix}\]

은 $P$의 eigenvector이고, 그때의 eigenvalue는 2입니다. 하지만

\[\begin{bmatrix}2&2\\0&1\end{bmatrix}\begin{bmatrix}0\\1\end{bmatrix} =\begin{bmatrix}2\\1\end{bmatrix}\]

은 어떻게 해도

\[x'=\begin{bmatrix}0\\1\end{bmatrix}\]

의 스칼라곱이 될 수 없으므로 $x’$는 eigenvector가 아닙니다.

$x$가 eigenvector이면 $x$의 스칼라곱인 $cx$도 eigenvector입니다$(c\ne0)$. 예를 들어, \(3x=\begin{bmatrix}3\\0\end{bmatrix}\)은 eigenvector입니다. 그리고 그 때의 eigenvalue는 여전히 $2$입니다;

\[\begin{bmatrix}2&2\\0&1\end{bmatrix}\begin{bmatrix}3\\0\end{bmatrix} =\begin{bmatrix}6\\0\end{bmatrix}=2\begin{bmatrix}3\\0\end{bmatrix}\]

이것은 일반적으로 성립합니다. 즉, 만약 $x$가 $A$의 eigenvector 라서 $Ax=\lambda x$이면,

\[A(cx)=cAx=c(\lambda x)=\lambda(cx)\]

이기 때문에 $cx$도 $A$의 eigenvalue입니다.

한편, 정의 15의 식

\[Ax=\lambda x\]

을 변형하면

\[\begin{align*} Ax&=\lambda(Ix)\\ Ax&=(\lambda I)x\\ Ax-(\lambda I)x&=0\\ (A-\lambda I)x&=0 \end{align*}\]

이 됩니다. 이 식으로부터 $\text{det}(A-\lambda I)=0$을 얻을 수 있습니다. 왜냐하면, 만약 $\text{det}(A-\lambda I)\ne0$일 경우, 정리 14(b)에 의하여 $A-\lambda I$의 역행렬이 존재합니다. 그러면

\[x=Ix=(A-\lambda I)^{-1}(A-\lambda I)x=(A-\lambda I)^{-1}0=0\]

이 되어 $x$가 영벡터가 아니라는 사실과 모순되기 때문입니다. 이상을 정리하면 다음과 같습니다.

성질 16
정사각행렬 $A$에 대하여
(a) $A$의 eigenvector가 $x$이면 스칼라곱인 $cx$도 eigenvector 입니다. (단, $c\ne0$).
(b) $Ax=\lambda x\:(x\ne0)$ 이기 위한 필요충분조건은 $(A-\lambda I)x=0$인 $x\ne0$이 존재하는 것입니다. 또 이것은 $\text{det}(A-\lambda I)=0$인 것과도 동치입니다.

성질 16(b)에서 식 $\text{det}(A-\lambda I)=0$을 characteristic equation(특성방정식)이라고 부릅니다.

예를 들어, 행렬

\[P=\begin{bmatrix}2&2\\0&1\end{bmatrix}\]

의 eigenvalue를 구하기 위해서는

\[\begin{align*} \text{det}(P-\lambda I)&=0\\[10pt] \begin{vmatrix}2-\lambda&2\\0&1-\lambda\end{vmatrix}&=0\\[10pt] (2-\lambda)(1-\lambda)-2\times0&=0\\[10pt] (\lambda-1)(\lambda-2)&=0 \end{align*}\]

을 풀면 됩니다. 이 이차방정식의 해는 1과 2이며, 그것들을 각각 $\lambda_1=1$, $\lambda_2=2$로 두겠습니다. 그리고 $\lambda_1$에 대응되는 eigenvector를 $x_1$으로, $\lambda_2$에 대응되는 eigenvector를 $x_2$으로 각각 표현하겠습니다. $x_1$을 구하기 위해 $x_1=\begin{bmatrix}a&b\end{bmatrix}^T$ 로 두면

\[\begin{align*} (P-\lambda_1I)x_1&=0\\[10pt] \begin{bmatrix}1&2\\0&0\end{bmatrix} \begin{bmatrix}a\\b\end{bmatrix}&=0 \end{align*}\]

이 됩니다. 이것은 연립방정식

\[\begin{cases} a+2b&=0\\ 0a+0b&=0 \end{cases}\]

을 푸는 것과 같으며, 따라서 $a=-2b$입니다. 그러므로 $x_1$은

\[x_1=\begin{bmatrix}a\\b\end{bmatrix} =\begin{bmatrix}-2b\\b\end{bmatrix} =b\begin{bmatrix}-2\\1\end{bmatrix}\]

입니다. 이때 성질 16(a)에 의해, $\lambda_1=1$에 대한 대표적인 eigenvector를

\[x_1=\begin{bmatrix}-2\\1\end{bmatrix}\]

라고 두어도 괜찮습니다. 마찬가지로 $x_2$를 구하면

\[\begin{align*} (P-\lambda_2I)x_2&=0\\[10pt] \begin{bmatrix}0&2\\0&-1\end{bmatrix} \begin{bmatrix}a\\b\end{bmatrix}&=0 \end{align*}\]

으로부터 $2b=0$이고, $-b=0$이고 따라서 $b=0$입니다. 따라서

\[\begin{bmatrix}a\\b\end{bmatrix} =\begin{bmatrix}a\\0\end{bmatrix} =a\begin{bmatrix}1\\0\end{bmatrix}\]

이고 $\lambda_2=2$에 대한 eigenvector $x_2$를

\[x_2=\begin{bmatrix}1\\0\end{bmatrix}\]

로 둘 수 있습니다.

다른 행렬들에 대해서도 eigenvalue / eigenvector를 구해보면 다음과 같습니다. (1.1 에서 정의한 $Q$, $R$ 등과 다른 행렬들입니다.) 행렬 $Q$가

\[Q=\begin{bmatrix}2&2\\2&-1\end{bmatrix}\]

이면

\[|Q-\lambda I| = \begin{vmatrix} 2-\lambda&2\\2&-1-\lambda \end{vmatrix} =(\lambda+2)(\lambda-3)=0\]

으로부터 $\lambda_1=-2$, $\lambda_2=3$이고,

\[\begin{align*} (Q-\lambda_1I)x_1&=0\\[10pt] \begin{bmatrix}4&2\\2&1\end{bmatrix} \begin{bmatrix}a\\b\end{bmatrix}&=0 \end{align*}\]

와

\[\begin{align*} (Q-\lambda_2I)x_2&=0\\[10pt] \begin{bmatrix}-1&2\\2&-4\end{bmatrix} \begin{bmatrix}a\\b\end{bmatrix}&=0 \end{align*}\]

에서

\[x_1=\begin{bmatrix}1\\-2\end{bmatrix},\quad x_2=\begin{bmatrix}2\\1\end{bmatrix}\]

입니다.

행렬 $R$이

\[R=\begin{bmatrix}3&2\\-4&-1\end{bmatrix}\]

이면

\[|R-\lambda I| = \begin{vmatrix} 3-\lambda&2\\-4&-1-\lambda \end{vmatrix} =\lambda^2-2\lambda+5=0\]

으로부터 $\lambda_1=1+2i$, $\lambda_2=1-2i$이고,

\[\begin{align*} (R-\lambda_1I)x_2&=0\\[10pt] \begin{bmatrix}2-2i&2\\-4&-2-2i\end{bmatrix} \begin{bmatrix}a\\b\end{bmatrix}&=0 \end{align*}\]

와

\[\begin{align*} (R-\lambda_2I)x_2&=0\\[10pt] \begin{bmatrix}2+2i&2\\-4&-2+2i\end{bmatrix} \begin{bmatrix}a\\b\end{bmatrix}&=0 \end{align*}\]

에서

\[x_1=\begin{bmatrix}1\\-1+i\end{bmatrix},\quad x_2=\begin{bmatrix}1\\-1-i\end{bmatrix}\]

입니다.

참고
$Q$의 첫번째 eigenvector는 $$x_1=\begin{bmatrix}-1\\2\end{bmatrix}$$ 로 두어도 상관없습니다. 마찬가지로 $R$의 두번째 eigenvector는 $$x_2=\begin{bmatrix}1-i\\-2\end{bmatrix}$$ 로 두어도 괜찮습니다. 이것들은 모두 기존 eigenvector의 실수배 혹은 복소수배입니다.

더 많은 예를 보기 전에, eigenvalue와 eigenvector가 어떤 의미를 가지는 지 간략하게 보려고 합니다. 이를 위해서는 먼저, 행렬이 일종의 함수라는 것을 받아들여야 합니다. 행렬

\[P=\begin{bmatrix}1&2\\0&2\end{bmatrix}\]

에 대하여 함수 $p$를

\[p(x)=Px\]

로 정의하면, $p$는 2차원 벡터

\[x=\begin{bmatrix}a\\b\end{bmatrix}\]

를 2차원 벡터

\[Px= \begin{bmatrix}2&2\\0&1\end{bmatrix}\begin{bmatrix}a\\b\end{bmatrix} =\begin{bmatrix}2a+2b\\b\end{bmatrix}\]

로 보내는 함수입니다. 몇 개의 함숫값들을 계산해보면

\[\begin{align*} p\left(\begin{bmatrix}2\\0\end{bmatrix}\right) &=\begin{bmatrix}4\\0\end{bmatrix}\\ p\left(\begin{bmatrix}0\\1\end{bmatrix}\right) &=\begin{bmatrix}2\\1\end{bmatrix}\\ p\left(\begin{bmatrix}4\\1\end{bmatrix}\right) &=\begin{bmatrix}10\\1\end{bmatrix} \end{align*}\]

등입니다.

참고
(a) 이 함수 $p$는 선형함수(linear function)입니다. 이것은, 함수 $p$가 덧셈과 스칼라곱을 보존하는 함수라는 뜻으로

• $p(x+y)=p(x)+p(y)$
• $p(cx)=cp(x)$

를 만족하는 함수라는 뜻입니다. (단, $x$, $y$는 2차원 벡터, $c$는 스칼라) 정의에 따라 계산해보면 위의 두 식이 성립함을 쉽게 확인할 수 있습니다.
(b) 증명하지는 않겠지만, 선형대수의 기본적인 사실 중 하나는 $n$차원 벡터를 $n$차원 벡터로 보내는 모든 선형함수는 행렬로 표현된다 는 것입니다. 다시 말해, 모든 행렬은 선형함수라고 간주할 수 있고, 모든 선형함수는 행렬로 표현할 수 있습니다. 그러니까 조금 비약해서 말하면, 행렬과 선형함수는 동일시할 수 있습니다.
(c) 선형함수는 수학에서 워낙 중요한 함수다보니, 여러 이름을 가지고 있습니다.

• 선형함수(linear function)
• 선형사상(linear map, linear mapping)
• 선형변환(linear transformation)
• 일차함수
• 일차변환

은 모두 같은 의미를 지칭하는 서로 다른 용어들입니다.
그러니까, 보통 중학교에서 배우는 $y=ax+b$와 같은 일차함수는 여기에서 말하는 선형함수와는 다른 의미입니다. 선형대수에서, 차원이 1인 선형함수는 $y=ax$ 뿐입니다. 일반적으로, $A$가 행렬이고 $x$, $y$, $b$가 벡터일 때 $y=Ax+b$와 같이 표현되는 함수는 'affine 함수'라고 불립니다. 그런 관점에서 본다면 함수 $y=ax+b$도 affine 함수라고 불러야 의미적으로 맞을 것입니다.

고등학교 수학에서 영벡터가 아닌 두 벡터가 서로 같은 방향(혹은 반대 방향)이면 한 벡터가 다른 벡터의 실수배와 같다는 것을 배웁니다. 행렬 $A$가 일종의 함수라는 관점에서 보면, eigenvector란, 함수 $A$에 의해 방향이 변하지 않는 벡터 (혹은 방향이 반대로 뒤집히는 벡터)를 의미합니다.

$x$가 행렬 $A$의 eigenvector이고 그에 대한 eigenvalue가 $\lambda>0$이면, 벡터 $x$는 함수 $A$에 의해 $Ax=\lambda x$로 변환됩니다. 이때 $Ax$는 $x$와 방향이 같고 그 길이가 $\lambda$배인 벡터를 의미하는 것입니다. 만약 $\lambda<0$이면, $Ax$는 $x$와 방향이 반대이고, 그 길이가 $\lambda$배인 벡터를 의미하는 것입니다.

예를 들어, 행렬

\[P=\begin{bmatrix}2&2\\0&1\end{bmatrix}\]

의 eigenvalue는 각각 $\lambda_1=1$, $\lambda_2=2$였고, 각각에 대응되는 eigenvector들은 $x_1=\begin{bmatrix}-2&1\end{bmatrix}^T$, $x_2=\begin{bmatrix}1&0\end{bmatrix}^T$ 이었습니다.

따라서 $P$에 대응되는 선형함수 $p$는 $x$축 방향의 벡터 $e_1=\begin{bmatrix}1&0\end{bmatrix}^T$를, 방향이 같으며 길이가 두 배인 벡터 $2e_1=\begin{bmatrix}2&0\end{bmatrix}^T$로 보냅니다. 즉,

\[p(e_1)=2e_1\]

입니다. 반면, $y$축 방향의 벡터 $e_2=\begin{bmatrix}0&1\end{bmatrix}^T$는 $e_2$와는 다른 방향인 $\begin{bmatrix}2&1\end{bmatrix}^T$로 보냅니다.

한편, $e_2$가 $e_2=x_1+2x_2$로 표현된다는 사실을 이용하면

\[p(e_2)=p(x_1+2x_2)=p(x_1)+2p(x_2)=x_1+4x_2 =\begin{bmatrix}-2\\1\end{bmatrix}+4\begin{bmatrix}1\\0\end{bmatrix} =\begin{bmatrix}2\\1\end{bmatrix}\]

와 같이 계산할 수도 있습니다. $p(e_2)$를 직접 계산하는 것에 비해 효율적이라고는 볼 수 없지만, 그래도 어떤 벡터 $x$에 대한 함수 $p$의 함숫값 $p(x)$를 계산할 때, eigenvector 측면에서 계산하면 재미있는 결과가 나온다는 것을 알 수 있습니다. 즉, 임의의 2차원벡터 $x$를 $x=\alpha_1x_1+\alpha_2x_2$의 형태로 놓으면

\[p(x)=\alpha_1p(x_1)+\alpha_2p(x_2) =\alpha_1\lambda_1x_1+\alpha_2\lambda_2x_2\]

와 같이 계산할 수 있는 것입니다. 평면벡터를 다룰 때 우리에게 익숙한 $x$축과 $y$축 방향 대신, 새로운 $x’$축과 $y’$축을 기준으로 계산할 수 있는데, 그 $x’$축의 방향과 $y’$축의 방향을 eigenvector들의 방향으로 정하면 그 계산이 쉬워진다는 뜻입니다.

이때, $P$의 경우에는 $x’$축의 방향 ($\begin{bmatrix}-2&1\end{bmatrix}^T$)과 $y’$축의 방향 ($\begin{bmatrix}1&0\end{bmatrix}^T$)이 서로 직교하지 않습니다. 반면에 $Q$에서는 $x’$축의 방향 ($\begin{bmatrix}1&-2\end{bmatrix}^T$)과 $y’$축의 방향 ($\begin{bmatrix}2&1\end{bmatrix}^T$)이 서로 직교합니다. 이러한 좌표변환에서 $Q$의 경우가 (orthogonally diagonalizable한 경우에 해당합니다.) $P$의 경우에 비해 (orthogonally diagonalizable하지 않은 경우에 해당합니다.) 더 계산이 편리할 것임은 지금 시점에서도 예상할 수 있습니다.

$P$, $Q$에서는 eigenvalue가 서로 다른 실수인 경우를, $R$에서는 eigenvalue가 서로 다른 허수인 경우를 보았습니다. 몇 개의 추가적인 예시를 통해 eigenvalue가 중복되는 경우($S$, $T$), $3\times3$인 경우($U$, $V$) 등에 대한 예시를 조금 더 살펴보겠습니다.

\[S=\begin{bmatrix} 1&3\\-3&-5 \end{bmatrix}\]

의 경우

\[|S-\lambda I|= \begin{vmatrix}1-\lambda&3\\-3&-5-\lambda\end{vmatrix}=(\lambda+2)^2=0\]

으로부터 $S$의 유일한 eigenvalue는 $\lambda=-2$임을 알 수 있습니다.

\[\begin{align*} \begin{bmatrix}3&3\\-3&-3\end{bmatrix} \begin{bmatrix}a\\b\end{bmatrix}&=0 \end{align*}\]

에서 $b=-a$이고

\[x_1=\begin{bmatrix}1\\-1\end{bmatrix}\]

입니다. 따라서, 모든 eigenvector는 $\begin{bmatrix}1&-1\end{bmatrix}^T$의 스칼라곱으로만 얻어진다는 것을 알 수 있습니다.

이때, 특성방정식 $(\lambda+2)^2=0$에서 근 $\lambda=-2$는 중근입니다. 즉, 서로 같은 실근입니다($\lambda_1=\lambda_2=-2$). 이와 같은 경우에 eigenvalue $\lambda=-2$에 대한 대수적 중복도(algebraic multiplicity)는 2라고 말합니다. 한편, $\lambda=-2$에 대응되는 모든 eigenvector는 하나의 벡터 $\begin{bmatrix}1&-1\end{bmatrix}^T$로 표현될 수 있었습니다. 이럴 때에, 기하적 중복도(geometric multiplicity)는 1이라고 말합니다.

$P$, $Q$, $R$의 예를 다시 살펴보면, eigenvalue가 중근을 가진 적이 없었으므로 algebraic multiplicity는 모두 1입니다. 그리고 각각의 eigenvalue에 대하여 모든 eigenvector들이 단 하나의 벡터에 대한 스칼라곱으로 표시될 수 있었기 때문에, geometric multiplicity도 모두 1입니다.

참고
이 포스트에서 소개하지 않는 선형대수 용어들을 동원하여 geometric multiplicity의 개념을 설명하자면 다음과 같습니다. $n\times n$ 행렬 $A$의 한 eigenvalue가 $\lambda$일 때, $A-\lambda I$의 null space $$N(A-\lambda I)=\{x:(A-\lambda I)x=0\}$$ 를 eigenvalue $\lambda$에 대한 eigenspace 라고 합니다. 이 eigenspace를 $\text{eig}(\lambda)$라고 적으면 $\text{eig}(\lambda)$는 $\mathbb R^n$의 subspace이고 그 dimension이 1 이상이며, eigenvector들은 $\text{eig}(\lambda)$의 basis를 형성합니다. 이때, $\text{eig}(\lambda)$의 dimension을 $\lambda$에 대한 geometric multiplicity라고 말할 수 있습니다. 즉, geometric multiplicity란, 특정한 eigenvalue $\lambda$에 대한 모든 eigenvector를 표현하기 위해 동원되어야 하는 최소한의 eigenvector들의 개수입니다.

다른 행렬

\[T=\begin{bmatrix} 3&0\\0&3 \end{bmatrix}\]

의 경우에도

\[|T-\lambda I|= \begin{vmatrix}3-\lambda&0\\0&3-\lambda\end{vmatrix} =(\lambda-3)^2=0\]

eigenvalue는 유일하게 하나($\lambda_1=\lambda_2=3$)로 주어집니다. eigenvector를 구하기 위해

\[\begin{align*} (R-3I)x&=0\\[10pt] \begin{bmatrix}0&0\\0&0\end{bmatrix} \begin{bmatrix}a\\b\end{bmatrix}&=0 \end{align*}\]

로 두면, $a$, $b$에 대한 아무런 정보도 얻을 수 없습니다. 즉, $a$와 $b$는 모두 임의의 실수이고, 모든 이차원 벡터

\[x=\begin{bmatrix}a\\b\end{bmatrix}\]

가 eigenvector의 역할을 할 수 있음을 확인할 수 있습니다. 한편, $x$가 다음과 같이 두 개의 벡터

\[x_1=\begin{bmatrix}1\\0\end{bmatrix},\qquad x_2=\begin{bmatrix}0\\1\end{bmatrix}\]

들의 일차결합(linear combination)

\[x=ax_1+bx_2\]

으로 표현될 수 있다는 사실을 생각해보면 두 개의 대표적인 eigenvector들을 각각 $x_1=\begin{bmatrix}1&0\end{bmatrix}^T$과 $x_2=\begin{bmatrix}0&1\end{bmatrix}^T$로 두어도 될 것입니다. 이 때에 algebraic multiplicity는 2이고 geometric multiplicity도 2입니다.

이번에는 $3\times 3$ 행렬

\[U=\begin{bmatrix} 2&0&1\\0&0&0\\1&0&2 \end{bmatrix}\]

에 대해서는

\[|U-\lambda I|= \begin{vmatrix}2-\lambda&0&1\\0&-\lambda&0\\1&0&2-\lambda\end{vmatrix}=-\lambda^3+4\lambda^2-3\lambda=-\lambda(\lambda-1)(\lambda-3)=0\]

에서 $\lambda_1=0$, $\lambda_2=1$, $\lambda_3=3$ 입니다.

\[\begin{align*} (U-0I)x&=0\\[10pt] \begin{bmatrix}2&0&1\\0&0&0\\1&0&2\end{bmatrix} \begin{bmatrix}a\\b\\c\end{bmatrix}&=0 \end{align*}\]

으로부터 $2a+c=0$, $a+2c=0$, $a=c=0$이고

\[x_1=\begin{bmatrix}0\\1\\0\end{bmatrix}\]

으로 둘 수 있습니다. 또한

\[\begin{align*} (U-I)x&=0\\[10pt] \begin{bmatrix}1&0&1\\0&-1&0\\1&0&1\end{bmatrix} \begin{bmatrix}a\\b\\c\end{bmatrix}&=0 \end{align*}\]

에서 $c=-a$, $b=0$이고

\[x_2=\begin{bmatrix}1\\0\\-1\end{bmatrix}\]

으로 둘 수 있습니다. 마지막으로

\[\begin{align*} (U-3I)x&=0\\[10pt] \begin{bmatrix}-1&0&1\\0&-3&0\\1&0&-1\end{bmatrix} \begin{bmatrix}a\\b\\c\end{bmatrix}&=0 \end{align*}\]

에서 $c=a$, $b=0$이고

\[x_3=\begin{bmatrix}1\\0\\1\end{bmatrix}\]

입니다. 따라서, $U$의 모든 eigenvalue들에 대하여 algebraic multiplicity와 geometric multiplicity는 모두 1입니다. 마지막 예시로서 행렬 $V$가

\[V=\begin{bmatrix} 0&0&2\\-3&1&6\\0&0&1 \end{bmatrix}\]

이면

\[|V-\lambda I|= \begin{vmatrix}-\lambda&0&2\\-3&1-\lambda&6\\0&0&1-\lambda\end{vmatrix}=-\lambda(\lambda-1)^2=0\]

에서 $\lambda_1=0$, $\lambda_2=\lambda_3=1$ 입니다.

\[\begin{align*} (V-0I)x&=0\\[10pt] \begin{bmatrix}0&0&2\\-3&1&6\\0&0&1\end{bmatrix} \begin{bmatrix}a\\b\\c\end{bmatrix}&=0 \end{align*}\]

으로부터 $c=0$, $-3a+b=0$, $b=3a$이고

\[x_1=\begin{bmatrix}1\\3\\0\end{bmatrix}\]

을 얻을 수 있습니다. $\lambda_2=\lambda_3=1$에 대해서는

\[\begin{align*} (V-I)x&=0\\[10pt] \begin{bmatrix}-1&0&2\\-3&0&6\\0&0&0\end{bmatrix} \begin{bmatrix}a\\b\\c\end{bmatrix}&=0 \end{align*}\]

에서 $-a+2c=0$, $a=2c$이고

\[x=\begin{bmatrix}2c\\b\\c\end{bmatrix} =c\begin{bmatrix}2\\0\\1\end{bmatrix} +b\begin{bmatrix}0\\1\\0\end{bmatrix}\]

이므로

\[\begin{align*} x_2&=\begin{bmatrix}2\\0\\1\end{bmatrix}\\ x_3&=\begin{bmatrix}0\\1\\0\end{bmatrix} \end{align*}\]

로 둘 수 있습니다. 이때, $\lambda_1=0$에 대한 algebraic multiplicity와 geometric multiplicity는 모두 1이고, $\lambda_2=\lambda_3=1$에 대한 algebraic multiplicity와 geometric multiplicity는 모두 2입니다.

참고
eigenvalue와 eigenvector는 선형대수를 응용하는 여러 방면에 쓰입니다. 이 포스트에서 다루는 바와 같이 직교대각화에 사용되고,선형적인 연립편미분방정식의 해를 구하는 데 쓰일 수 있으며, 머신러닝의 SVD(singular value decomposition), PCA(principal component analysis)의 계산에서도 나타나고, 행렬의 norm을 계산하는 데에도 등장합니다.

2.2 대각화와 직교대각화

이제 이 포스트의 주된 주제인 대각화(diagonalization)와 직교대각화(orthogonal/unitary diagonalization)에 대해 말할 수 있습니다.

정의 17 : 행렬의 대각화와 직교대각화
정사각행렬 $A$에 대하여
(a) $A=BDB^{-1}$을 만족시키는 대각행렬 $D$와 가역행렬 $B$가 존재하면 $A$가 대각화가능(diagonalizable)하다고 말합니다.
(b) $A$가 실수행렬이고 $A=BDB^{-1}$를 만족시키는 대각행렬 $D$와 orthogonal 행렬 $B$가 존재하면 $A$가 직교대각화가능(orthogonally diagonalizable)하다고 말합니다.
(c) $A$가 복소행렬이고 $A=BDB^{-1}$를 만족시키는 대각행렬 $D$와 unitary 행렬 $B$가 존재하면 $A$를 직교대각화가능 (unitarily diagonalizable)하다고 말합니다.

이 포스트에서는 orthogonal diagonalization과 unitary diagonalization을 모두 ‘직교대각화’라는 한국어로 지칭했습니다. 경우에 따라서는 후자를 ‘유니터리대각화’라는 말로 번역하기도 하는 것 같지만, 너무 긴 용어라고 판단되어서 사용하지 않겠습니다. 그러니까, 어떤 행렬에 대하여 ‘직교대각화’라는 말을 쓸 때 그 행렬이 실수행렬이면 orthogonal diagonalization에 대해 말하는 것이고, 그 행렬이 복소행렬이면 unitary diagonalization을 말하는 것입니다.

1.4에서 eigenvalue/eigenvector의 의미에 대해 설명하면서 좌표변환에 대해 간략하게 언급했습니다. 어떤 행렬 $A$에 대한 좌표변환은 [정확하게는, 행렬 $A$의 열들이 basis를 이룰 때, 그 basis에 대한 좌표변환(change of basis)는] 그 행렬의 왼쪽에 가역행렬 $B$를 곱함으로써 얻어질 수 있습니다. 그런 의미에서 식

\[A=BDB^{-1}\]

의 양변은 어떤 종류의 선형함수(선형변환)인데, 이 함수에 $x$를 넣으면

\[Ax=BDB^{-1}x=B\left(D\left(B^{-1}(x)\right)\right)\]

이 됩니다. 좌표변환 $B$가 $x’y’$좌표계를 $xy$좌표계로 바꾸는 것이라고 할 때, $B^{-1}$는 $xy$좌표계를 $x’y’$좌표계로 바꾸는 것입니다. 따라서, $B\left(D\left(B^{-1}(x)\right)\right)$를 계산하는 것은 $x$의 좌표를 $xy$좌표계에서 $x’y’$좌표계로 바꾼 뒤 바뀐 좌표계에서 간단한 함수 $D$를 취한 뒤, 그것을 다시 $x’y’$좌표계에서 $xy$좌표계로 돌리는 것과 같습니다.

그러니까 조금 과장해서 말하면,

좌표변환 $B$를 거치고 나면 행렬 $A$가 대각행렬 $D$로 변환된다.

라고 할 수 있습니다. 그런 의미에서 대각화란, 주어진 행렬을 간단한 형태로 변환하는 것을 의미합니다.

일반 행렬 $A$에 비해 대각행렬 $D$는, 특히 거듭제곱의 관점에서, 다루기 쉬운 행렬입니다. 즉,

\[D=\begin{bmatrix} \lambda_1 &\cdots &0\\ \vdots &\ddots &\vdots\\ 0 &\cdots &\lambda_n \end{bmatrix}\]

이면

\[D^k=\begin{bmatrix} {\lambda_1}^k&\cdots &0\\ \vdots &\ddots &\vdots\\ 0 &\cdots &{\lambda_n}^k \end{bmatrix}\]

임을 쉽게 증명할 수 있습니다. 따라서, 만약 $A$를 $A=BDB^{-1}$로 쓸 수 있다면, $A$의 거듭제곱인 $A^k$도

\[\begin{align*} A^k &=\left(BDB^{-1}\right)^2\\ &=\left(BDB^{-1}\right)\left(BDB^{-1}\right)\cdots\left(BDB^{-1}\right)\\ &=BD^kB^{-1} \end{align*}\]

와 같이 비교적 간단하게 계산될 수 있습니다.

만약, $A$가 대각화가능하다고 해도, 좌표변환한 축들이 서로 수직한 경우가 더 ‘바람직’합니다. 이러한 행렬을 직교대각화가능한 행렬이라고 부르는 것인데, 어떤 행렬 $A$가 직교대각화가능할 경우, 좌표변환을 관장하는 행렬인 $B$가 orthogonal 행렬이므로 (혹은 unitary 행렬이므로) 그 역행렬을 구하는 것도 매우 간단해집니다. ($B^{-1}=B^T$ 또는 $B^{-1}=B^H$, 이하 성질 08(c), 성질 12(c))

대부분의 행렬들은 대각화가 가능합니다. 그리고 대각화 과정은 그 행렬의 eigenvalue와 eigenvector를 이용함으로써 쉽게 얻어질 수 있습니다. 앞서

\[P=\begin{bmatrix}2&2\\0&1\end{bmatrix}\]

에 대하여

\[\begin{align*} \lambda_1&=1,&\quad x_1&=\begin{bmatrix}-2\\1\end{bmatrix}\\ \lambda_2&=2,&\quad x_2&=\begin{bmatrix}1\\0\end{bmatrix} \end{align*}\]

로 계산했었습니다. 정의에 의해

\[Px_1=\lambda_1x_1,\quad Px_2=\lambda_2x_2\]

혹은

\[\begin{bmatrix}2&2\\0&1\end{bmatrix} \begin{bmatrix}-2\\1\end{bmatrix} = 1 \begin{bmatrix}-2\\1\end{bmatrix} ,\quad \begin{bmatrix}2&2\\0&1\end{bmatrix} \begin{bmatrix}1\\0\end{bmatrix} = 2 \begin{bmatrix}1\\0\end{bmatrix}\]

가 성립하는 것인데 이것을 하나의 식

\[\begin{bmatrix}2&2\\0&1\end{bmatrix} \begin{bmatrix}-2&1\\1&0\end{bmatrix} = \begin{bmatrix}-2&1\\1&0\end{bmatrix} \begin{bmatrix}1&0\\0&2\end{bmatrix}\]

으로 표현할 수 있는 것입니다. 따라서 $P$는 대각화가능합니다;

\[P= \begin{bmatrix}2&2\\0&1\end{bmatrix} = BDB^{-1} = \begin{bmatrix}-2&1\\1&0\end{bmatrix} \begin{bmatrix}1&0\\0&2\end{bmatrix} \begin{bmatrix}-2&1\\1&0\end{bmatrix}^{-1}\]

이때, $D$의 대각성분들은 eigenvalue들로 채워지게 되고 $B$의 열들은 eigenvector들로 채워집니다. 그런 의미에서 $D$를 eigenvalue matrix라고 부르기도 하고, $B$를 eigenvector matrix라고 부르기도 합니다.

마찬가지로,

\[Q=\begin{bmatrix}2&2\\2&-1\end{bmatrix}\]

는

\[\begin{align*} \lambda_1&=-2, &\quad x_1&=\begin{bmatrix}1\\-2\end{bmatrix}\\ \lambda_2&=3, &\quad x_2&=\begin{bmatrix}2\\1\end{bmatrix} \end{align*}\]

이고

\[Q \begin{bmatrix} |&|\\ x_1&x_2\\ |&| \end{bmatrix} = \begin{bmatrix} -2&0\\0&3 \end{bmatrix} \begin{bmatrix} |&|\\ x_1&x_2\\ |&| \end{bmatrix}\]

입니다. 따라서 $Q$도 대각화가능합니다;

\[Q= \begin{bmatrix}2&2\\2&-1\end{bmatrix} = BDB^{-1} = \begin{bmatrix}1&2\\-2&1\end{bmatrix} \begin{bmatrix}-2&0\\0&3\end{bmatrix} \begin{bmatrix}1&2\\-2&1\end{bmatrix}^{-1}\]

또한, eigenvalue가 허수였던 행렬

\[R=\begin{bmatrix}3&2\\-4&-1\end{bmatrix}\]

도

\[\begin{align*} \lambda_1&=1+2i, &\quad x_1&=\begin{bmatrix}1\\-1+i\end{bmatrix}\\ \lambda_2&=1-2i, &\quad x_2&=\begin{bmatrix}1\\-1-i\end{bmatrix} \end{align*}\]

에서

\[R= \begin{bmatrix}3&2\\-4&-1\end{bmatrix} = BDB^{-1} = \begin{bmatrix}1&1\\-1+i&-1-i\end{bmatrix} \begin{bmatrix}1+2i&0\\0&1-2i\end{bmatrix} \begin{bmatrix}1&1\\-1+i&-1-i\end{bmatrix}^{-1}\]

입니다.

지금까지 $2\times 2$ 행렬에 대한 대각화를 시도해보았고, $P$, $Q$, $R$이 모두 대각화가능하다는 것을 볼 수 있었습니다. 특히 $Q$의 경우에는 $B$가 orthogonal 행렬이므로 직교대각화가 가능한 행렬이라는 것을 알 수 있습니다.

한편, 행렬

\[S=\begin{bmatrix} 1&3\\-3&-5 \end{bmatrix}\]

의 경우, 유일한 eigenvalue $\lambda=-2$를 가졌었습니다.

\[\lambda_1=\lambda_2=-2,\quad x_1=\begin{bmatrix}1\\-1\end{bmatrix}\]

만약 $x_2$를 $x_2=x_1$으로 둔다면,

\[Sx_1=\lambda_1x_1,\quad Sx_2=\lambda_2x_2,\] \[S \begin{bmatrix} |&|\\ x_1&x_2\\ |&| \end{bmatrix} = \begin{bmatrix} -2&0\\0&-2 \end{bmatrix} \begin{bmatrix} |&|\\ x_1&x_2\\ |&| \end{bmatrix} = \begin{bmatrix} -2&0\\0&-2 \end{bmatrix} \begin{bmatrix} 1&1\\ -1&-1 \end{bmatrix}\]

로 두어 $SB=DB$와 같은 식을 만들 수는 있습니다. 하지만,

\[B=\begin{bmatrix}1&1\\-1&-1\end{bmatrix}\]

이 비가역행렬이므로 $S=BDB^{-1}$와 같이 만들 수 없습니다. $S$는 diagonalizable한지 판단할 수 없습니다.

반면, 행렬

\[T=\begin{bmatrix} 3&0\\0&3 \end{bmatrix}\]

는

\[\begin{align*} \lambda_1&=3, &\quad x_1&=\begin{bmatrix}1\\0\end{bmatrix}\\ \lambda_2&=3, &\quad x_2&=\begin{bmatrix}0\\1\end{bmatrix} \end{align*}\]

이기 때문에, $S$에서와 마찬가지로 eigenvalue의 algebraic multiplicity가 2이지만, 이 경우에는 대각화가능합니다. $P$, $Q$, $R$, $S$에서와 같은 과정을 통해서도 대각화 식을 얻을 수 있지만, $T$는 그 자체로 대각행렬이기 때문에 대각화가능하다고 볼 수 있습니다. 즉

\[T= \begin{bmatrix}3&0\\0&3\end{bmatrix} = IDI^{-1} = \begin{bmatrix}1&0\\0&1\end{bmatrix} \begin{bmatrix}3&0\\0&3\end{bmatrix} \begin{bmatrix}1&0\\0&1\end{bmatrix}^{-1}\]

인 것입니다.

위의 예들을 통해서 보면 충분한 수의 eigenvector가 생긴다면, 대각화가 가능하리라고 판단할 수 있습니다. 이는 다음과 같이 정리될 수 있습니다.

성질 18
$n\times n$ 행렬 $A$에 대하여 $A$의 각 eigenvalue들에 대한 geometric multiplicity의 합이 $n$이면, $A$는 대각화가능합니다.

(‘선형독립’의 정의를 내린 적은 없지만) 다시 말해, $A$가 선형독립인 $n$개의 eigenvector를 가진다면, $A$는 대각화가능합니다.

다음의 $3\times 3$행렬 $U$, $V$도 충분한 geometric multiplicity를 가지므로 모두 대각화가능합니다. 특히, $U$는 eigenvector들이 pairwisely orthogonal하므로 orthogonal diagonalization도 가능합니다.

\[U=\begin{bmatrix}2&0&1\\0&0&0\\1&0&2\end{bmatrix}\] \[\lambda_1=0,\quad x_1=\begin{bmatrix}0\\1\\0\end{bmatrix},\qquad \lambda_2=1,\quad x_2=\begin{bmatrix}1\\0\\-1\end{bmatrix},\qquad \lambda_3=3,\quad x_3=\begin{bmatrix}1\\0\\1\end{bmatrix}\] \[\begin{align*} U&= \begin{bmatrix} 0&1&1\\ 1&0&0\\ 0&-1&1 \end{bmatrix} \begin{bmatrix} 0&0&0\\ 0&1&0\\ 0&0&3 \end{bmatrix} \begin{bmatrix} 0&1&1\\ 1&0&0\\ 0&-1&1 \end{bmatrix}^{-1}\\ &= \begin{bmatrix} 0&1&1\\ 1&0&0\\ 0&-1&1 \end{bmatrix} \begin{bmatrix} 0&0&0\\ 0&1&0\\ 0&0&3 \end{bmatrix} \begin{bmatrix} 0&1&0\\ 1&0&-1\\ 1&0&1 \end{bmatrix} \end{align*}\] \[V=\begin{bmatrix}0&0&2\\-3&1&6\\0&0&1\end{bmatrix}\] \[\lambda_1=0,\quad x_1=\begin{bmatrix}1\\3\\0\end{bmatrix},\qquad \lambda_2=1,\quad x_2=\begin{bmatrix}2\\1\\0\end{bmatrix},\qquad \lambda_3=1,\quad x_3=\begin{bmatrix}0\\0\\1\end{bmatrix}\]

또한, 행렬 $V$에 대해서는

\[\begin{align*} V&= \begin{bmatrix} 1&2&0\\ 3&1&0\\ 0&0&1 \end{bmatrix} \begin{bmatrix} 0&0&0\\ 0&1&0\\ 0&0&1 \end{bmatrix} \begin{bmatrix} 1&2&0\\ 3&1&0\\ 0&0&1 \end{bmatrix}^{-1} \end{align*}\]

행렬의 직교대각화에 관한 기본적인 정리이자, 이 포스트의 목적이기도 한 두 명제는 다음과 같습니다.

정리 19
정사각행렬 $A$에 대하여
(a) $A$가 실수 행렬이고 symmetric 행렬이면 $A$는 orthogonally diagonalizable합니다.
(b) $A$가 복소 행렬이고 Hermitian 행렬이면 $A$는 unitarily diagonalizable합니다.

실제로, 위의 예시들에서 $Q$, $U$는 real symmetric 행렬(실수 행렬이면서 symmetric) 이었고, orthogonally diagonalizable했습니다.

한편, 위의 정리에서 (b)만 증명하면 (a)도 증명하는 셈이 됩니다. 이것은 성질 21에서 따로 증명하겠습니다. 따라서, 남은 포스트의 내용은 정리 19(b)를 증명하는 것을 목적으로 합니다. 그러면 정리 19를 모두 증명하는 셈이 됩니다. 그리고 사실 원래 만들었던 파일의 내용은 지금부터이며, 앞의 내용들은 이 증명을 위한 배경지식이었습니다.

만약, 행렬 $A$의 eigenvalue들이 모두 다를 경우에 정리 19(b)를 증명하는 것은 그래도 꽤 간결하게 설명될 수 있습니다 (2.3). 하지만, 그렇지 않을 경우, 즉 characteristic equation이 중근을 가질 경우까지 고려한다면 그렇게 간단하지 않아서, Schur’s lemma를 사용해 설명해보았습니다 (2.4). 이 부분들은 Gilbert Strang의 「Linear Algebra and its Applications」 (4판, 2006)을 참고하여 적은 것임을 밝힙니다.

2.3 증명 1 : distinct eigenvalues

성질 20
정사각행렬 $A$에 대하여 $A$가 Hermitian이면 다음 사실이 성립합니다.
(a) $x^HAx$는 실수입니다.
(b) $A$의 eigenvalue들은 모두 실수입니다
(c) 만약 $A$의 eigenvalue들이 모두 다르다면, eigenvector들은 pairwisely orthogonal합니다.

(a)에 대해 증명하기 전에, $2\times2$의 경우를 간단히 보겠습니다. $A$가 Hermitian이므로

\[A=\begin{bmatrix}a&b\\\overline b&c\end{bmatrix}\]

로 둘 수 있습니다. 이때, $a$, $b$, $c$는 모두 복소수입니다. 그러면, $x^HAx$는 각각 $1\times 2$, $2\times2$, $2\times 1$ 행렬이므로 행렬곱 연산이 가능하고, 그 결과는 $1\times1$ 행렬로 이것을 하나의 복소수로 취급할 수 있습니다.

\[x=\begin{bmatrix}u\\v\end{bmatrix}\]

로 두고 계산하면

\[x^HAx= \begin{bmatrix}\overline u&\overline v\end{bmatrix} \begin{bmatrix}a&b\\\overline b&c\end{bmatrix} \begin{bmatrix}u\\v\end{bmatrix} =a\overline uu+\overline bu\overline v+b\overline uv+c\overline vv =a|u|^2+(\overline bu\overline v+b\overline uv)+c|v|^2\]

이 됩니다. 첫번째 항과 마지막 항은 당연히 실수이고, 가운데 괄호의 두 개 항은 켤레 관계인 두 복소수의 합이므로 여전히 실수입니다. 따라서 $x^HAx$는 항상 실수입니다.

$A$가 $2\times2$인 특정한 경우가 아닌 일반적인 상황에에 대한 증명은, 지금까지의 설명보다도 훨씬 짧습니다. $x^HAx$가 $1\times1$ 행렬임을 상기하고 이것의 conjugation을 계산하면 (성질 02(c), (d) 등에 의해)

\[\overline{\left(x^HAx\right)}=\overline{\left(x^HAx\right)}^T=\left(x^HAx\right)^H=x^HA^H(x^H)^H=x^HAx.\]

입니다. $x^HAx$의 conjugation을 취한 것이 자기 자신과 같으므로 $x^HAx$는 실수입니다.

(b)의 증명도 어렵지 않습니다. $\lambda$를 $A$의 한 eigenvalue라고 하겠습니다. 우리는 $\lambda$가 실수임을 증명하기만 하면 됩니다. eigenvalue의 정의(정의 15)에 의해

\[Ax=\lambda x\]

를 만족시키는 벡터 $x$가 존재합니다$(x\ne0)$. 이 식의 양변의 왼쪽에 $x^H$를 곱하면

\[x^HAx=x^H(\lambda x)=\lambda x^Hx=\lambda\cdot||x||^2\]

가 됩니다. $x\ne0$이므로 $||x||\ne0$이고, (a)에 의해

\[\lambda=\frac{x^HAx}{||x||^2}\]

는 실수입니다.

(c)의 증명은 다음과 같습니다. $A$의 두 eigenvector를 각각 $x_1$, $x_2$라고 하고, 대응되는 eigenvalue들을 각각 $\lambda_1$, $\lambda_2$라고 하겠습니다 ($\lambda_1\ne\lambda_2$). $Ax_1=\lambda_1x_1$, $Ax_2=\lambda_2x_2$ 입니다. 그러면

\[\begin{align*} \lambda_1{x_1}^Hx_2 &=\overline{\lambda_1}{x_1}^Hx_2=\left(\lambda_1{x_1}\right)^Hx_2=\left(Ax_1\right)^Hx_2\\ &=({x_1}^HA^H)x_2=({x_1}^HA)x_2={x_1}^H(Ax_2)\\ &={x_1}^H(\lambda_2x_2)=\lambda_2{x_1}^Hx_2 \end{align*}\]

입니다. 즉

\[\left(\lambda_1-\lambda_2\right){x_1}^Hx_2=0\]

이고, $\lambda_1\ne\lambda_2$ 로부터

\[{x_1}^Hx_2=0\]

입니다. 다시 말해, $x_1$과 $x_2$의 내적 $\langle x_1, x_2 \rangle$가 0이라는 말이므로 $x_1$과 $x_2$는 orthogonal합니다. 그러니까, 임의의 두 eigenvector $x_1$, $x_2$가 orthogonal하므로 (c)가 증명된 셈입니다. $\square$

위의 세 성질을 이용하면, characteristic equation의 근이 모두 다를 경우(중근이 없는 경우)에 대한 정리 19(b)의 증명은 다음과 같이 될 수 있습니다.

증명 : $A$가 $n\times n$ Hermitian 행렬이고, $n$개의 서로 다른 eigenvalue들을 가지면 $A$는 unitarilly diagonalizable 합니다.

$A$의 서로 다른 eigenvalue들을 $\lambda_1$, $\cdots$, $\lambda_n$이라고 하고 각각에 대응되는 eigenvector들을 $x_1$, $\cdots$, $x_n$이라고 하면, $i=1,\cdots,n$에 대하여

\[Ax_i=\lambda_ix_i\]

가 성립합니다. 성질 20(c)에 의해 $x_i$들은 pairwisely orthogonal합니다. 그런데 $x_i$들의 스칼라곱도 여전히 eigenvector이므로 (성질 16(a)), $x_i$들의 norm이 모두 1이라고 가정할 수 있습니다. 즉 $x_i$들이 orthonormal하다고 말할 수 있습니다. 이제 2.2 에서 여러 행렬들에 대해서 했던 것과 비슷하게 하면

\[B=\begin{bmatrix}|&&|\\x_1&\cdots&x_n\\|&&|\end{bmatrix}\]

는 unitary 행렬이고 (성질 08(a))

\[\begin{align*} AB&=A\begin{bmatrix}|&&|\\x_1&\cdots&x_n\\|&&|\end{bmatrix} =\begin{bmatrix}Ax_1&\cdots&Ax_n\end{bmatrix} =\begin{bmatrix}\lambda_1x_1&\cdots&\lambda_nx_n\end{bmatrix}\\ &=\begin{bmatrix}|&&|\\x_1&\cdots&x_n\\|&&|\end{bmatrix} \begin{bmatrix}\lambda_1&\cdots&0\\\vdots&\ddots&\vdots\\0&\cdots&\lambda_n\end{bmatrix} =BD \end{align*}\]

입니다. 따라서 $A=BDB^H$이고 $A$는 unitarily diagonalizable합니다. $\square$

성질 21
정리 19의 (b)가 성립하면 (a)도 성립합니다.

(b)가 성립한다고 가정하고 $A$가 real symmetric 하다고 두면 $A$는 Hermitian 행렬이기도 합니다$(A^H={\overline A}^T=A^T=A)$. 따라서 (b)에 의해 $A$는 $A=BDB^{-1}$를 만족시키는 unitary 행렬 $B$가 존재합니다.

하지만 아직 $A$가 orthogonally diagonalizable한 것은 아닙니다. $B$는 unitary 행렬이기 때문에 허수가 포함된 행렬일 수도 있습니다. 만약 $B$가 허수가 포함된 행렬이라면 $A$가 orthogonally diagonally diagonalizable하다고 말할 수 없겠지만, $B$가 순수하게 실수로만 이루어진 행렬이라면 $A$가 orthogonally diagonallizable하다고 말할 수 있습니다. 그러니까, $B$가 실수로만 이루어진 행렬이라는 것만 증명할 수 있으면 됩니다. 그리고 $B$가 실수행렬이라는 것을 증명하기 위해서는 $A$의 모든 eigenvector들이 실수벡터임을 보이기만 하면 됩니다.

$x$가 $A$의 eigenvector일 때, $x$를 $x=x_1+x_2i$로 두면 ($x_1$, $x_2$는 각각 $n$차원의 실수벡터) $x\ne0$이므로 $x_1\ne0$ 이거나 $x_2\ne0$ 입니다.

\[Ax=\lambda x\]

에서

\[Ax_1+iAx_2=\lambda x_1+i\lambda x_2\]

입니다. 이때, 성질 20(b)에 의해 $\lambda$는 실수이고, 가정에 의해 $A$가 실수행렬이므로

\[Ax_1=\lambda x_1,\quad Ax_2=\lambda x_2\]

입니다. 그런데 $x_1$과 $x_2$ 중 하나는 0이 아니라고 했습니다. 일반성을 잃지 않고 $x_1\ne0$이라고 하면, $x_1$은 $\lambda$의 eigenvector입니다. 따라서 $B$가 실수행렬이라는 것이 증명되었습니다.

다시 말해, $B$는 unitary 행렬인데 orthogonal 행렬이기도 합니다(1.4의 마지막 참고). 그러니까, $A$는 unitarily diagonalizable할 뿐만 아니라 orthogonally diagonalizable하기도 한 것입니다. $\square$

2.4 증명 2 : repeated roots

이전 절에서 정리 19(b)를, characteristic equation이 중근을 가지지 않는 경우 (eigenvalue들이 겹치지 않는 경우)에 한해 증명했습니다. 또한 정리 19(b)가 성립하면 정리 19(a)도 성립한다고 했으므로 characteristic equation이 중근을 가지지 않는 경우에 대해서는 정리 19를 모두 증명한 셈입니다. 이제는 eigenvalue가 겹치는 경우, 즉 characteristic equation이 중근을 가질 수도 있는 일반적인 경우에 대한 정리 19의 증명을 해보겠습니다. 이번에도, 19(b)만 증명하면, 19(a)도 증명한 셈이 됩니다.

증명해야 할 명제를 다시 쓰면

$A$가 복소 행렬이고 Hermitian 행렬이면 $A$는 unitarily diagonalizable합니다.

입니다. 이 명제는 Schur’s lemma (성질 25)를 사용할 수 있으면 쉽게 증명될 수 있습니다. 하지만 Schur’s lemma를 설명하기 위해서는 similiarity(정의 22)와 Gram-Schmidt process(성질 24)에 대해 먼저 살펴봐야 합니다.

similarity

정의 22
두 대각행렬 $A_1$, $A_2$에 대하여 $$A_2=BA_1B^{-1}$$ 을 만족시키는 가역행렬 $B$가 존재하면, $A_1$와 $A_2$가 similar(유사)하다고 말합니다.

이 이항관계(binary operation)는 동치관계(equivalence relation)이기도 합니다. 즉, 대각행렬 $A$, $B$, $C$에 대하여 (a) $A\sim A$이고, (b) $A\sim B$이면 $B\sim A$이고 (c) $A\sim B$ 이고 $B\sim C$이면, $A\sim C$입니다. 따라서 모든 $n\times n$ 행렬들을 이 similarity에 의해 분류할 수도 있습니다.

한편, 정의 17에서의 대각화식 $A=BDB^{-1}$은

$A$와 $D$가 유사하다.

라는 말로 표현할 수도 있습니다. 또한, 그런 관점에서 보면, similar한 두 행렬들이란 좌표변환을 통해 같아질 수 있는 행렬이라고도 말할 수 있습니다.

중요한 사실 중 하나는, similar한 행렬들이 같은 eigenvalue들을 공유한다는 점입니다.

성질 23
$\lambda$가 $A_1$의 eigenvalue이고 $A_2=BA_1B^{-1}$이면 $\lambda$는 $A_2$의 eigenvalue입니다. 그리고 $\lambda$에 대한 $A_1$의 eigenvector가 $x$이면, $A_2$의 eigenvector는 $B^{-1}x$입니다.

증명 : 성질 23

만약 $A_1x=\lambda x$이면 $A_1=BA_2B^{-1}$로부터

\[BA_2B^{-1}x=\lambda x\]

이고 양변의 왼쪽에 $B^{-1}$를 곱하면

\[A_2(B^{-1}x)=B^{-1}(\lambda x)=\lambda(B^{-1}x)\]

이기 때문입니다. $\square$

Gram-Schmidt process

다음으로 Gram-Schmidt process입니다. 다만, 일반적으로 선형대수에서 이야기되는 Gram-Schmidt process 대신, 조금 특수한 경우의 Gram-Schmidt process를 이야기하려 합니다.

성질 24
$n$차원 벡터 $x_1$, $\cdots$, $x_k$가 orthonormal이면 ($k\lt n$) $n-k$개의 벡터 $x_{k+1}$, $\cdots$, $x_n$이 존재하여 $x_1$, $\cdots$, $x_n$이 orthonormal하도록 만들 수 있습니다.

증명 : 성질 24

orthonormal한 $x_1$, $\cdots$, $x_k$에 대하여 $\langle{x_j},x_{k+1}\rangle=0$, $||x_{k+1}||=1$을 만족시키는 $x_{k+1}$만 찾아낼 수 있으면 됩니다(단, $j=1,\cdots,k$). 그러면 $x_1$, $\cdots$, $x_k$, $x_{k+1}$은 orthonormal하고, 이 orthonormal 벡터들에 대하여 같은 작업을 반복할 수 있기 때문입니다.

$e_i$를, $i$번째 성분이 1이고 나머지 성분이 0인 벡터라고 하겠습니다. 이 벡터들은 standard unit vector (표준단위벡터)라고 부릅니다. 예를 들어, 3차원공간에서는

\[e_1=\begin{bmatrix}1\\0\\0\end{bmatrix},\quad e_2=\begin{bmatrix}0\\1\\0\end{bmatrix},\quad e_3=\begin{bmatrix}0\\0\\1\end{bmatrix}\]

입니다. $k<n$ 이므로, $e_i\notin\{x_1,\cdots,x_k\}$를 만족시키는 $i$가 존재합니다. $\hat x_{k+1}$을

\[\hat x_{k+1}=e_i-\langle x_1,e_i\rangle x_1-\langle x_2,e_i\rangle x_2-\cdots-\langle x_k,e_i\rangle x_k\]

로 정의합니다. 그러면, $j=1,2,\cdots,k$에 대하여 $\hat x_{k+1}\perp x_j$입니다;

\[\begin{align*} \langle x_j,\hat x_{k+1}\rangle &=\langle x_j, e_i-\langle x_1,e_i\rangle x_1-\langle x_2,e_i\rangle x_2-\cdots-\langle x_k,e_i\rangle x_k\rangle\\ &=\langle x_j, e_i\rangle -\langle x_1,e_i\rangle\langle x_j,x_1\rangle -\langle x_2,e_i\rangle\langle x_j,x_2\rangle -\cdots -\langle x_k,e_i\rangle\langle x_j,x_k\rangle\\ &=\langle x_j, e_i\rangle-\langle x_j,e_i\rangle\langle x_j,x_j\rangle\\ &=0 \end{align*}\]

이 계산에서, $\langle x,y+z\rangle=\langle x,y\rangle+\langle x,z\rangle$, $\langle x, cy\rangle=c\langle x,y\rangle$과 같은 성질들이 사용되었습니다(정의 9에 딸린 참고). 이제, $\hat x_{k+1}$을 크기가 1인 벡터로 만들면 $x_{k+1}$이 얻어집니다;

\[x_{k+1}=\frac{\hat x_{k+1}}{||\hat x_{k+1}||}.\]

이로써, 성질 24이 증명되었습니다. $\square$

참고
조금 더 일반적인, 보통의 Gram-schmidt process라 함은 다음과 같습니다
innper product space (혹은 $\mathbb R^n$, $\mathbb C^n$) 에서의 $m$개의 벡터 $v_1$, $v_2$, $\cdots$, $v_m$가 선형독립일 때, $$\text{span}(v_1,v_2,\cdots,v_m)=\text{span}(u_1,u_2,\cdots,u_m)$$ 를 만족시키는 orthonormal한 $m$개의 벡터 $u_1$, $u_2$, $\cdots$, $u_m$ 가 존재합니다. $u_i$를 얻어내는 방식은 성질 24에서와 거의 유사합니다. 먼저 $u_1$는 $u_1=\frac{v_1}{||v_1||}$으로 정합니다. 따라서 $u_1$은 크기가 1인 벡터입니다. $u_1$, $\cdots$, $u_k$가 주어졌을 때 ($k\lt n$) $u_{k+1}$은 $$ \begin{align*} \hat x_{k+1}&=v_{k+1} -\langle u_1,v_{k+1}\rangle u_1 -\langle u_2,v_{k+1}\rangle u_2 -\cdots -\langle u_k,v_{k+1}\rangle u_k\\ x_{k+1}&=\frac{\hat x_{k+1}}{||\hat x_{k+1}||} \end{align*} $$ 로 정하면 됩니다.

예를 들어, 4차원 실수벡터 $x_1$, $x_2$가

\[x_1=\frac1{\sqrt6}\begin{bmatrix}1\\1\\2\\0\end{bmatrix} ,\quad x_2=\frac1{\sqrt6}\begin{bmatrix}2\\0\\-1\\1\end{bmatrix}\]

이라고 하면, $x_1$과 $x_2$는 orthonormal합니다. $e_1\notin\{x_1,x_2\}$이므로

\[\begin{align*} \hat x_3 &=e_1-\langle x_1,e_1\rangle x_1-\langle x_2,e_1\rangle x_2\\ &=\begin{bmatrix}1\\0\\0\\0\end{bmatrix} -\frac1{\sqrt6}\cdot\frac1{\sqrt6}\begin{bmatrix}1\\1\\2\\0\end{bmatrix} -\frac2{\sqrt6}\cdot\frac1{\sqrt6}\begin{bmatrix}2\\0\\-1\\1\end{bmatrix} \\ &=\begin{bmatrix}1\\0\\0\\0\end{bmatrix} -\begin{bmatrix}\frac16\\\frac16\\\frac26\\0\end{bmatrix} -\begin{bmatrix}\frac46\\0\\-\frac26\\\frac26\end{bmatrix}\\ &=\frac16\begin{bmatrix}1\\-1\\0\\-2\end{bmatrix} \end{align*}\]

입니다. 이것을 크기가 1인 벡터로 만들면

\[x_3=\frac{x_3}{||x_3||} =\frac1{\sqrt6}\begin{bmatrix}1\\-1\\0\\-2\end{bmatrix}\]

이 됩니다. 마찬가지로, $e_2\notin\{x_1,x_2,x_3\}$이므로

\[\begin{align*} \hat x_4 &=e_2-\langle x_1,e_2\rangle x_1-\langle x_2,e_2\rangle x_2-\langle x_3,e_2\rangle x_3\\ &=\begin{bmatrix}0\\1\\0\\0\end{bmatrix} -\frac1{\sqrt6}\cdot\frac1{\sqrt6}\begin{bmatrix}1\\1\\2\\0\end{bmatrix} -0 +\frac1{\sqrt6}\cdot\frac1{\sqrt6}\begin{bmatrix}1\\-1\\0\\2\end{bmatrix} \\ &=\begin{bmatrix}0\\1\\0\\0\end{bmatrix} -\begin{bmatrix}\frac16\\\frac16\\\frac26\\0\end{bmatrix} +\begin{bmatrix}\frac16\\-\frac16\\0\\-\frac26\end{bmatrix}\\ &=\frac16\begin{bmatrix}0\\4\\-2\\-2\end{bmatrix} \end{align*}\]

이고

\[x_4=\frac{x_4}{||x_4||} =\frac1{\sqrt6}\begin{bmatrix}0\\2\\-1\\-1\end{bmatrix}\]

입니다. 그러면, 정말로 네 벡터 $x_1$, $x_2$, $x_3$, $x_4$는 orthonormal합니다.

Schur’s Lemma

성질 25 : Schur's Lemma
대각행렬 $A$에 대하여 $U^{-1}AU$가 상삼각행렬인 unitary 행렬 $U$가 존재합니다.

이때, 상삼각행렬(upper triangular matrix)이란, 행렬의 대각성분들의 아래에 있는 모든 성분들이 0인 행렬을 말합니다. 아래에 정의된 $T_1$, $T_2$는 모두 상삼각행렬입니다.

\[T_1=\begin{bmatrix}2&5\\0&-1\end{bmatrix},\qquad T_2=\begin{bmatrix}-1&0&3\\0&2&4\\0&0&0\end{bmatrix}\]

증명 : 성질 25 (Schur’s lemma)

$A$가 $n\times n$ 행렬이라고 하겠습니다. $A$의 characteristic equation $|A-\lambda I|=0$은 계수가 복소수인 $n$차 방정식이므로, $n$개의 근 $\lambda_1$, $\lambda_2$, $\cdots$, $\lambda_n$을 가집니다. (이것은 대수학의 기본정리(fundamental theorem of algebra)에 의해 그렇습니다.) $\lambda_1$의 eigenvector 중 크기가 1인 벡터를 $x_1$이라고 하겠습니다. 성질 24에 의해, $x_1$을 포함하는 orthonormal한 $n$개의 벡터를 만들 수 있고 이 벡터들을 열벡터로 나열하여 unitary 행렬 $U_1$을 만들 수 있습니다. $x_1$을 $U_1$의 첫번째 열에 두면, $Ax_1=\lambda_1x_1$으로부터

\[\begin{align*} \begin{bmatrix} a_{11}&a_{12}&a_{13}&\cdots&a_{1n}\\ a_{21}&a_{22}&a_{23}&\cdots&a_{2n}\\ a_{31}&a_{32}&a_{33}&\cdots&a_{3n}\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ a_{n1}&a_{n2}&a_{n3}&\cdots&a_{nn} \end{bmatrix} \begin{bmatrix} | &* &* &\cdots&* \\ | &* &* &\cdots&* \\ x_1 &* &* &\cdots&* \\ | &\vdots&\vdots&\ddots&\vdots\\ | &* &* &\cdots&* \end{bmatrix} &= \begin{bmatrix} | &* &* &\cdots&* \\ | &* &* &\cdots&* \\ x_1 &* &* &\cdots&* \\ | &\vdots&\vdots&\ddots&\vdots\\ | &* &* &\cdots&* \end{bmatrix} \begin{bmatrix} \lambda_1&* &* &\cdots&* \\ 0 &* &* &\cdots&* \\ 0 &* &* &\cdots&* \\ 0 &\vdots&\vdots&\ddots&\vdots\\ 0 &* &* &\cdots&* \end{bmatrix}\\ AU_1&=U_1A_1\qquad(n\times n) \end{align*}\]

이 됩니다. $A_1$의 오른쪽 아래에 있는 $n-1\times n-1$ 행렬을 $A^{(1)}$이라고 하겠습니다. 즉

\[A_1= \begin{bmatrix} \lambda_1&* &* &\cdots&* \\ 0 &* &* &\cdots&* \\ 0 &* &* &\cdots&* \\ 0 &\vdots&\vdots&\ddots&\vdots\\ 0 &* &* &\cdots&* \end{bmatrix} = \begin{bmatrix} \lambda_1&*\\ 0 &A^{(1)} \end{bmatrix}\]

입니다. $A_1$은 첫 대각성분이 $\lambda_1$이고 그 아래가 모두 0인 행렬입니다. 이때, $A_1\sim A$이므로 $A_1$은 $\lambda_1$, $\lambda_2$, $\cdots$, $\lambda_n$을 eigenvalue로 갖습니다(성질 22). 그리고 행렬식의 정의를 잘 생각해보면 $A^{(1)}$은 $\lambda_2$, $\cdots$, $\lambda_n$을 eigenvalue로 갖습니다.

이제 $A^{(1)}$에 방금 $A$에 했던 것과 비슷한 작업을 합니다. $A^{(1)}$에서 $\lambda_2$의 eigenvector를 $x_2$라고 하면 $x_2$를 포함하는 $n-1$개의 orthonormal벡터를 만들 수 있고, 이것들을 열벡터로 나열하여 $n-1\times n-1$인 unitary 행렬 $U^{(2)}$를 만들 수 있습니다. $x_2$를 $U^{(2)}$의 첫번째 열에 두면

\[\begin{align*} \begin{bmatrix} * &* &\cdots&* \\ * &* &\cdots&* \\ \vdots&\vdots&\ddots&\vdots\\ * &* &\cdots&* \end{bmatrix} \begin{bmatrix} | &* &\cdots&* \\ x_2 &* &\cdots&* \\ | &\vdots&\ddots&\vdots\\ | &* &\cdots&* \end{bmatrix} &= \begin{bmatrix} | &* &\cdots&* \\ x_2 &* &\cdots&* \\ | &\vdots&\ddots&\vdots\\ | &* &\cdots&* \end{bmatrix} \begin{bmatrix} \lambda_2&* &\cdots&* \\ 0 &* &\cdots&* \\ 0 &\vdots&\ddots&\vdots\\ 0 &* &\cdots&* \end{bmatrix}\\ A^{(1)}U^{(2)}&=U^{(2)}A^{(2)}\qquad(n-1\times n-1) \end{align*}\]

입니다. $n-1\times n-1$행렬 $A^{(2)}$와 $U^{(2)}$를 가지고 각각 $A_2$와 $U_2$를

\[\begin{align*} U_2&= \begin{bmatrix} 1 &0\\ 0 &U^{(2)} \end{bmatrix} = \begin{bmatrix} 1 &0 &0 &\cdots&0 \\ 0 &| &* &\cdots&* \\ 0 &x_2 &* &\cdots&* \\ \vdots&| &\vdots&\ddots&\vdots\\ 0 &| &* &\cdots&* \end{bmatrix} \\ A_2&= \begin{bmatrix} \lambda_1&* \\ 0 &A^{(2)} \end{bmatrix} = \begin{bmatrix} \lambda_1&* &* &\cdots&* \\ 0 &\lambda_2&* &\cdots&* \\ 0 &0 &* &\cdots&* \\ \vdots&\vdots&\vdots&\ddots&\vdots\\ 0 &0 &* &\cdots&* \end{bmatrix} \end{align*}\]

와 같이 만들면, $A_2$는 처음 두 개의 대각성분들이 $\lambda_1$, $\lambda_2$이고 그 아래가 모두 0인 행렬입니다. 그리고 $U_2$는 unitary 행렬입니다. 또한,

\[\begin{align*} \begin{bmatrix} 1 &* \\ 0 &A^{(1)} \end{bmatrix} \begin{bmatrix} 1 &* \\ 0 &U^{(2)} \end{bmatrix} &= \begin{bmatrix} 1 &* \\ 0 &U^{(2)} \end{bmatrix} \begin{bmatrix} \lambda_1&* \\ 0 &A^{(2)} \end{bmatrix}\\ A_1U_2&=U_2A_2 \end{align*}\]

즉, $A_1\sim A_2$가 성립합니다. $A_2$의 오른쪽 아래에 있는 $n-2\times n-2$ 행렬을 $A^{(2)}$라고 하면

\[A_2= \begin{bmatrix} \lambda_1&* &* &\cdots&* \\ 0 &\lambda_2&* &\cdots&* \\ 0 &0 &* &\cdots&* \\ \vdots&\vdots&\vdots&\ddots&\vdots\\ 0 &0 &* &\cdots&* \end{bmatrix} = \begin{bmatrix} \lambda_1&* &* \\ 0 &\lambda_2&*\\ 0 &0 &A^{(2)} \end{bmatrix}\]

입니다. 다시, $A_2$는 $\lambda_1$, $\cdots$, $\lambda_n$을 eigenvalue로 가지고, 따라서 $A^{(2)}$는 $\lambda_3$, $\cdots$, $\lambda_n$을 eigenvalue로 가집니다. $A^{(2)}$에서 $\lambda_3$의 eigenvector를 $x_3$라고 하면 $x_3$를 포함하는 $n-2$개의 orthonormal벡터를 만들 수 있고, 이것들을 열벡터로 나열하여 $n-2\times n-2$인 unitary 행렬 $U^{(3)}$를 만들 수 있습니다. $x_3$를 $U^{(3)}$의 첫번째 열에 두면

\[\begin{align*} \begin{bmatrix} * &\cdots&* \\ \vdots&\ddots&\vdots\\ * &\cdots&* \end{bmatrix} \begin{bmatrix} | &\cdots&* \\ x_3 &\ddots&\vdots\\ | &\cdots&* \end{bmatrix} &= \begin{bmatrix} | &\cdots&* \\ x_3 &\ddots&\vdots\\ | &\cdots&* \end{bmatrix} \begin{bmatrix} \lambda_3&\cdots &* \\ \vdots&\ddots&\vdots\\ 0 &\cdots&* \end{bmatrix}\\ A^{(2)}U^{(3)}&=U^{(3)}A^{(3)}\qquad(n-2\times n-2) \end{align*}\]

입니다. $n-2\times n-2$ 행렬 $U^{(3)}$, $A^{(3)}$을 가지고 $n\times n$ 행렬 $U_3$, $A_3$를

\[\begin{align*} U_3&= \begin{bmatrix} 1 &0 &0\\ 0 &1 &*\\ 0 &0 &U^{(3)} \end{bmatrix} = \begin{bmatrix} 1 &0 &0 &\cdots&0 \\ 0 &1 &* &\cdots&* \\ 0 &0 &| &\cdots&* \\ \vdots&\vdots&x_3 &\ddots&\vdots\\ 0 &0 &| &\cdots&* \end{bmatrix} \\ A_3&= \begin{bmatrix} \lambda_1&* &*\\ 0 &\lambda_2&*\\ 0 &0 &A^{(3)} \end{bmatrix} = \begin{bmatrix} \lambda_1&* &* &\cdots&* \\ 0 &\lambda_2&* &\cdots&* \\ 0 &0 &\lambda_3&\cdots&* \\ \vdots&\vdots&\vdots&\ddots&\vdots\\ 0 &0 &0 &\cdots&* \end{bmatrix} \end{align*}\]

와 같이 만들면, $A_3$는 처음 두 개의 대각성분들이 $\lambda_1$, $\lambda_2$, $\lambda_3$이고 그 아래가 모두 0인 행렬입니다. 그리고 $U_3$는 unitary 행렬입니다. 또한,

\[\begin{align*} \begin{bmatrix} \lambda_1&* &* \\ 0 &\lambda_2&*\\ 0 &0 &A^{(2)} \end{bmatrix} \begin{bmatrix} 1 &* &*\\ 0 &1 &*\\ 0 &0 &U^{(3)} \end{bmatrix} &= \begin{bmatrix} 1 &* &*\\ 0 &1 &*\\ 0 &0 &U^{(3)} \end{bmatrix} \begin{bmatrix} \lambda_1&* &*\\ 0 &\lambda_2&*\\ 0 &0 &A^{(3)} \end{bmatrix}\\ A_2U_3&=U_3A_3 \end{align*}\]

이 성립합니다. 또다시, $A_2\sim A_3$가 성립하고 이와 같은 과정을 반복할 수 있습니다. $k$번의 반복 후에 처음 $k$개의 대각성분들이 $\lambda_1$, $\lambda_2$, $\cdots$, $\lambda_k$이고, 그 아래가 모두 0인 행렬 $A_k$를 얻을 수 있고,$U_1$, $\cdots$, $U_{k-1}$은 모두 unitary 행렬입니다. $A_{k-1}$는 $A$와

\[AU_1=U_1A_1,\quad A_1U_2=U_2A_2,\quad \cdots, A_{k-2}U_{k-1}=U_{k-1}A_{k-1},\quad\]

의 관계를 가집니다. 그러면

\[\begin{align*} A &={U_1}A_1{U_1}^{-1}\\ &=\cdots\\ &=U_1\cdots U_{k-1}A_{k-1}{U_{k-1}}^{-1}\cdots {U_1}^{-1}\\ \end{align*}\]

입니다.

$n-1$번의 반복 후에는

대각성분들이 $\lambda_1$, $\lambda_2$, $\cdots$, $\lambda_{n-1}$인 상삼각행렬 $A_{n-1}$을 얻을 수 있고 $A_{n-1}$은 $A$와

\[\begin{align*} A &=U_1\cdots U_{n-1}A_{n-1}{U_{n-1}}^{-1}\cdots {U_1}^{-1}\\ &=U_1\cdots U_{n-1}A_{n-1}\left(U_1\cdots U_{n-1}\right)^{-1} \end{align*}\]

의 관계식을 가집니다. 행렬 $U$를 $U=(U_1\cdots U_{n-1})^{-1}$로 두면, $U$는 unitary 행렬이고

\[A_{n-1}=UAU^{-1}\]

입니다. 정리하면, $UAU^{-1}$이 상삼각행렬이 되는 unitary 행렬 $U$를 찾은 셈입니다. 따라서 Schur’s lemma가 증명되었습니다. $\square$

예시 : Schur’s lemma

$3\times3$ 행렬 $A$를

\[A= \begin{bmatrix} 2&1&-2\\ 1&0&0\\ 0&1&0 \end{bmatrix}\]

으로 두겠습니다. $A$는 symmetric하지는 않기 때문에 orthogonally diagonalizable하다고 볼 수는 없습니다. 하지만 모든 정사각행렬에 대해서 Schur’s lemma는 성립하므로 $A=UA_2U^{-1}$을 만족시키는 unitary 행렬 $U$와 상삼각행렬 $A_2$를 만들어 볼 수는 있습니다. 그 과정은 다음과 같습니다.

이 행렬의 characteristic equation은

\[\begin{align*} |A-\lambda I| &=(2-\lambda)(-\lambda)(-\lambda)-1\cdot1\cdot(-\lambda)+(-2)\cdot1\cdot1\\ &=(2-\lambda)(\lambda^2-1) \end{align*}\]

이므로 $\lambda_1=1$, $\lambda_2=-1$, $\lambda_3=2$로 둘 수 있습니다. $\lambda_1=1$에 대한 eigenvector $x_1$을 구하기 위해

\[\begin{gather*} (A-\lambda I)x_1=0\\[10pt] \begin{bmatrix} 1&1&-2\\ 1&-1&0\\ 0&1&-1 \end{bmatrix} \begin{bmatrix} a\\b\\c \end{bmatrix} = \begin{bmatrix} 0\\0\\0 \end{bmatrix} \end{gather*}\]

을 풀면 $a+b-2c=0$, $a-b=0$, $b-c=0$에서 $a=b=c$이고 $\begin{bmatrix}1&1&1\end{bmatrix}^T$은 $\lambda_1$의 한 eigenvector입니다. 이 eigenvector의 크기를 1로 만들면

\[x_1=\frac1{\sqrt3}\begin{bmatrix}1\\1\\1\end{bmatrix}\]

이 됩니다. 이제 $U_1$을 만들어야 합니다. 즉, $x_1$을 포함하여 세 개의 3차원 벡터들이 orthonormal하도록 만들어야 합니다. 이를 위해서는 Gram-Schmidt process를 사용해도 되지만, 이 경우에는 식이 간단하므로, 나머지 두 벡터를 ${x_1}^{(2)}=\begin{bmatrix}a&b&c\end{bmatrix}^T$, ${x_1}^{(3)}=\begin{bmatrix}d&e&f\end{bmatrix}^T$로 두면 $\langle{x_1},{x_1}^{(2)}\rangle=0$, $\langle{x_1},{x_1}^{(3)}\rangle=0$, $\langle{x_1}^{(2)},{x_1}^{(3)}\rangle=0$ 으로부터

\[\begin{align*} a+b+c&=0\\ d+e+f&=0\\ ad+be+cf&=0 \end{align*}\]

를 만족시킵니다. 이 식을 만족시키는 정수 $a$, $\cdots$, $f$를 먼저 찾겠습니다. $a=1$, $b=-1$, $c=0$이면 첫번째 식 $a+b+c=0$을 만족시킵니다. 또한,

\[\begin{align*} d+e+f&=0\\ d-e&=0 \end{align*}\]

에서 $d=1$, $e=1$, $f=-2$로 둘 수 있습니다. 따라서

\[\begin{align*} x_1= &\frac1{\sqrt3}\begin{bmatrix}1&1&1\end{bmatrix}^T,\\ {x_1}^{(2)}= &\begin{bmatrix}1&-1&0\end{bmatrix}^T,\\ {x_1}^{(3)}= &\begin{bmatrix}1&1&-2\end{bmatrix}^T \end{align*}\]

는 pairwisely orthogonal 조건을 만족시키는 세 벡터입니다. 이제 뒤의 두 벡터의 크기를 1로 바꾸어

\[\begin{align*} x_1= &\frac1{\sqrt3}\begin{bmatrix}1&1&1\end{bmatrix}^T,\\ {x_1}^{(2)}= &\frac1{\sqrt2}\begin{bmatrix}1&-1&0\end{bmatrix}^T,\\ {x_1}^{(3)}= &\frac1{\sqrt6}\begin{bmatrix}1&1&-2\end{bmatrix}^T \end{align*}\]

으로 만들면 이 벡터들은 orthonormal합니다. 이 벡터들을 열벡터로 하는 unitary 행렬 $U_1$은

\[U_1= \begin{bmatrix} \frac1{\sqrt3} &\frac1{\sqrt2} &\frac1{\sqrt6} \\ \frac1{\sqrt3} &-\frac1{\sqrt2} &\frac1{\sqrt6} \\ \frac1{\sqrt3} &0 &-\frac2{\sqrt6} \end{bmatrix}\]

입니다. 그러면, 첫번째 열의 대각성분이 $\lambda_1=1$이고 그 아래가 모두 0인 행렬 $A_1$이 존재하여

\[AU_1=U_1A_1\]

입니다. 이것을 더 자세히 쓰면

\[\begin{bmatrix} 2&1&-2\\ 1&0&0\\ 0&1&0 \end{bmatrix} \begin{bmatrix} \frac1{\sqrt3} &\frac1{\sqrt2} &\frac1{\sqrt6} \\ \frac1{\sqrt3} &-\frac1{\sqrt2} &\frac1{\sqrt6} \\ \frac1{\sqrt3} &0 &-\frac2{\sqrt6} \end{bmatrix} = \begin{bmatrix} \frac1{\sqrt3} &\frac1{\sqrt2} &\frac1{\sqrt6} \\ \frac1{\sqrt3} &-\frac1{\sqrt2} &\frac1{\sqrt6} \\ \frac1{\sqrt3} &0 &-\frac2{\sqrt6} \end{bmatrix} \begin{bmatrix} 1&*&*\\ 0&*&*\\ 0&*&* \end{bmatrix}\]

입니다. 다음단계로 가기 전에, $A_1$을 먼저 구해놓겠습니다.

\[\begin{align*} A_1 &=\begin{bmatrix} 1&*&*\\ 0&*&*\\ 0&*&* \end{bmatrix}\\ &= \begin{bmatrix} \frac1{\sqrt3} &\frac1{\sqrt2} &\frac1{\sqrt6} \\ \frac1{\sqrt3} &-\frac1{\sqrt2} &\frac1{\sqrt6} \\ \frac1{\sqrt3} &0 &\frac-2{\sqrt6} \end{bmatrix}^{-1} \begin{bmatrix} 2&1&-2\\ 1&0&0\\ 0&1&0 \end{bmatrix} \begin{bmatrix} \frac1{\sqrt3} &\frac1{\sqrt2} &\frac1{\sqrt6} \\ \frac1{\sqrt3} &-\frac1{\sqrt2} &\frac1{\sqrt6} \\ \frac1{\sqrt3} &0 &\frac-2{\sqrt6} \end{bmatrix}\\ &= \begin{bmatrix} \frac1{\sqrt3} &\frac1{\sqrt2} &\frac1{\sqrt6} \\ \frac1{\sqrt3} &-\frac1{\sqrt2} &\frac1{\sqrt6} \\ \frac1{\sqrt3} &0 &\frac2{\sqrt6} \end{bmatrix}^T \begin{bmatrix} 2&1&-2\\ 1&0&0\\ 0&1&0 \end{bmatrix} \begin{bmatrix} \frac1{\sqrt3} &\frac1{\sqrt2} &\frac1{\sqrt6} \\ \frac1{\sqrt3} &-\frac1{\sqrt2} &\frac1{\sqrt6} \\ \frac1{\sqrt3} &0 &\frac2{\sqrt6} \end{bmatrix}\\ &= \begin{bmatrix} \frac1{\sqrt3} &\frac1{\sqrt3} &\frac1{\sqrt3} \\ \frac1{\sqrt2} &-\frac1{\sqrt2} &0 \\ \frac1{\sqrt6} &\frac1{\sqrt6} &\frac2{\sqrt6} \end{bmatrix} \begin{bmatrix} 2&1&-2\\ 1&0&0\\ 0&1&0 \end{bmatrix} \begin{bmatrix} \frac1{\sqrt3} &\frac1{\sqrt2} &\frac1{\sqrt6} \\ \frac1{\sqrt3} &-\frac1{\sqrt2} &\frac1{\sqrt6} \\ \frac1{\sqrt3} &0 &\frac2{\sqrt6} \end{bmatrix}\\ &= \begin{bmatrix} 1 &\frac1{\sqrt6} &\frac3{\sqrt2} \\ 0 &0 &\sqrt3 \\ 0 &\frac2{\sqrt3} &1 \end{bmatrix} \end{align*}\]

입니다. 이제, $A_1$의 오른쪽 아래 $2\times2$ 행렬을 $A^{(1)}$로 두겠습니다. 다시 말해,

\[A_1 =\begin{bmatrix} 1 &\frac1{\sqrt6} &\frac3{\sqrt2} \\ 0 &0 &\sqrt3 \\ 0 &\frac2{\sqrt3} &1 \end{bmatrix} =\begin{bmatrix}1&*\\0&A^{(1)}\end{bmatrix}\]

이고

\[A^{(1)}= \begin{bmatrix} 0 &\sqrt3 \\ \frac2{\sqrt3} &1 \end{bmatrix}\]

인 것입니다.

이때, $A_1$과 $A_2$는 similar하므로 $A_2$의 eigenvalue들은 ($A$일때와 마찬가지로) $\lambda_1=1$, $\lambda_2=-1$, $\lambda_3=2$입니다. 또한, 행렬의 구조상 $A^{(1)}$의 eigenvalue들은 $\lambda_2=-1$, $\lambda_3=2$ 입니다. $A^{(1)}$의 eigenvalue $\lambda_2=-1$에 대한 eigenvector $x_2$는

\[\begin{bmatrix} 1 &\sqrt3 \\ \frac2{\sqrt3} &2 \end{bmatrix} \begin{bmatrix} a\\b \end{bmatrix} =0\]

으로부터 구할 수 있고, $a=-\sqrt 3b$로부터 eigenvector $\begin{bmatrix}-\sqrt3&1\end{bmatrix}^T$를 얻을 수 있습니다. 이것의 크기를 1로 바꾸면

\[x_2= \begin{bmatrix} -\frac{\sqrt3}2\\\frac12 \end{bmatrix}\]

를 얻을 수 있습니다.

$x_2$와 함께 orthonormal 조건을 만족시키는 벡터를 $\begin{bmatrix}a&b\end{bmatrix}^T$

라고 하면

\[-\sqrt3a+b=0\]

와 $b=\sqrt3a$에서 이 벡터를 $\begin{bmatrix}1&\sqrt3\end{bmatrix}^T$로 둘 수 있고, 이것의 크기를 1로 두어 ${x_2}^{(2)}=\begin{bmatrix}\frac12&\frac{\sqrt3}2\end{bmatrix}^T$로 둘 수 있습니다. 다시 말해, 두 벡터

\[\begin{align*} x_2&= \begin{bmatrix} -\frac{\sqrt3}2&\frac12 \end{bmatrix}^T\\ {x_2}^{(2)}&= \begin{bmatrix} \frac12&\frac{\sqrt3}2 \end{bmatrix}^T\end{align*}\]

는 orthonormal합니다. 이 벡터들을 열벡터로 하는 행렬

\[U^{(2)}= \begin{bmatrix} -\frac{\sqrt3}2 &\frac12 \\ \frac12 &\frac{\sqrt3}2 \end{bmatrix}\]

는 unitary 행렬이고,

\[A^{(1)}U^{(2)}=U^{(2)}A^{(2)}\]

인 상삼각행렬 $A^{(2)}$가 존재합니다. 이것을 자세히 쓰면

\[\begin{bmatrix} 0 &\sqrt3 \\ \frac2{\sqrt3} &1 \end{bmatrix} \begin{bmatrix} -\frac{\sqrt3}2 &\frac12 \\ \frac12 &\frac{\sqrt3}2 \end{bmatrix} = \begin{bmatrix} -\frac{\sqrt3}2 &\frac12 \\ \frac12 &\frac{\sqrt3}2 \end{bmatrix} \begin{bmatrix} -1 &* \\ 0 &* \end{bmatrix}\]

입니다. 아까와 마찬가지로 $A^{(2)}$를 계산을 통해 구하면

\[\begin{align*} A^{(2)} &= \begin{bmatrix} -1 &* \\ 0 &* \end{bmatrix}\\ &= \begin{bmatrix} -\frac{\sqrt3}2 &\frac12 \\ \frac12 &\frac{\sqrt3}2 \end{bmatrix}^{-1} \begin{bmatrix} 0 &\sqrt3 \\ \frac2{\sqrt3} &1 \end{bmatrix} \begin{bmatrix} -\frac{\sqrt3}2 &\frac12 \\ \frac12 &\frac{\sqrt3}2 \end{bmatrix}\\ &= \begin{bmatrix} -\frac{\sqrt3}2 &\frac12 \\ \frac12 &\frac{\sqrt3}2 \end{bmatrix}^T \begin{bmatrix} 0 &\sqrt3 \\ \frac2{\sqrt3} &1 \end{bmatrix} \begin{bmatrix} -\frac{\sqrt3}2 &\frac12 \\ \frac12 &\frac{\sqrt3}2 \end{bmatrix}\\ &= \begin{bmatrix} -\frac{\sqrt3}2 &\frac12 \\ \frac12 &\frac{\sqrt3}2 \end{bmatrix} \begin{bmatrix} 0 &\sqrt3 \\ \frac2{\sqrt3} &1 \end{bmatrix} \begin{bmatrix} -\frac{\sqrt3}2 &\frac12 \\ \frac12 &\frac{\sqrt3}2 \end{bmatrix}\\ &= \begin{bmatrix} -1 &-\frac1{\sqrt3} \\ 0 &2 \end{bmatrix} \end{align*}\]

이제, 두 개의 $2\times2$ 행렬 $U^{(2)}$, $A^{(2)}$를 가지고 $3\times3$ 행렬

\[\begin{align*} U_2 &= \begin{bmatrix} 1&0\\ 0&U^{(2)} \end{bmatrix} = \begin{bmatrix} 1&0&0\\ 0&-\frac{\sqrt3}2 &\frac12\\ 0&\frac12 &\frac{\sqrt3}2 \end{bmatrix}\\ A_2 &= \begin{bmatrix} 1&*\\ 0&A^{(2)} \end{bmatrix} = \begin{bmatrix} 1&*&*\\ 0&-1 &-\frac1{\sqrt3} \\ 0&0 &2 \end{bmatrix} \end{align*}\]

을 얻으면, $U_2$는 unitary 행렬이고

\[A_1U_2=U_2A_2\]

입니다. 이것으로 $A_2$를 구하면

\[\begin{align*} A_2 &={U_2}^{-1}A_1U_2\\ &= \begin{bmatrix} 1&0&0\\ 0&-\frac{\sqrt3}2 &\frac12\\ 0&\frac12 &\frac{\sqrt3}2 \end{bmatrix}^{-1} \begin{bmatrix} 1 &\frac1{\sqrt6} &\frac3{\sqrt2} \\ 0 &0 &\sqrt3 \\ 0 &\frac2{\sqrt3} &1 \end{bmatrix} \begin{bmatrix} 1&0&0\\ 0&-\frac{\sqrt3}2 &\frac12\\ 0&\frac12 &\frac{\sqrt3}2 \end{bmatrix}\\ &= \begin{bmatrix} 1&0&0\\ 0&-\frac{\sqrt3}2 &\frac12\\ 0&\frac12 &\frac{\sqrt3}2 \end{bmatrix} \begin{bmatrix} 1 &\frac1{\sqrt6} &\frac3{\sqrt2} \\ 0 &0 &\sqrt3 \\ 0 &\frac2{\sqrt3} &1 \end{bmatrix} \begin{bmatrix} 1&0&0\\ 0&-\frac{\sqrt3}2 &\frac12\\ 0&\frac12 &\frac{\sqrt3}2 \end{bmatrix}\\ &=\begin{bmatrix} 1&0 &0\\ 0&-1&-\frac1{\sqrt3} \\ 0&0 &2 \end{bmatrix} \end{align*}\]

입니다. 따라서

\[A=U_1A_1{U_1}^{-1}=U_1U_2A_2\left(U_1U_2\right)^{-1}\]

입니다. 이때,

\[U=U_1U_2= \begin{bmatrix} \frac1{\sqrt3} &\frac1{\sqrt2} &\frac1{\sqrt6} \\ \frac1{\sqrt3} &-\frac1{\sqrt2} &\frac1{\sqrt6} \\ \frac1{\sqrt3} &0 &-\frac2{\sqrt6} \end{bmatrix} \begin{bmatrix} 1&0&0\\ 0&-\frac{\sqrt3}2 &\frac12\\ 0&\frac12 &\frac{\sqrt3}2 \end{bmatrix} = \begin{bmatrix} \frac1{\sqrt3} &-\frac1{\sqrt6} &\frac1{\sqrt2}\\ \frac1{\sqrt3} &\frac2{\sqrt6} &0\\ \frac1{\sqrt3} &-\frac1{\sqrt6} &-\frac1{\sqrt2} \end{bmatrix}\]

는 unitary행렬입니다. 최종적인 직교대각화식 $A=UA_2U^{-1}$을 다시 써보면

\[\begin{align*} \begin{bmatrix} 2&1&-2\\ 1&0&0\\ 0&1&0 \end{bmatrix} &= \begin{bmatrix} \frac1{\sqrt3} &-\frac1{\sqrt6} &\frac1{\sqrt2}\\ \frac1{\sqrt3} &\frac2{\sqrt6} &0\\ \frac1{\sqrt3} &-\frac1{\sqrt6} &-\frac1{\sqrt2} \end{bmatrix}^{-1} \begin{bmatrix} 1&0 &0\\ 0&-1&-\frac1{\sqrt3} \\ 0&0 &2 \end{bmatrix} \begin{bmatrix} \frac1{\sqrt3} &-\frac1{\sqrt6} &\frac1{\sqrt2}\\ \frac1{\sqrt3} &\frac2{\sqrt6} &0\\ \frac1{\sqrt3} &-\frac1{\sqrt6} &-\frac1{\sqrt2} \end{bmatrix}\\ &= \begin{bmatrix} \frac1{\sqrt3} &\frac1{\sqrt3} &\frac1{\sqrt3} \\ -\frac1{\sqrt6} &\frac2{\sqrt6} &-\frac1{\sqrt6} \\ \frac1{\sqrt2} &0 &-\frac1{\sqrt2} \end{bmatrix} \begin{bmatrix} 1&0 &0\\ 0&-1&-\frac1{\sqrt3} \\ 0&0 &2 \end{bmatrix} \begin{bmatrix} \frac1{\sqrt3} &-\frac1{\sqrt6} &\frac1{\sqrt2}\\ \frac1{\sqrt3} &\frac2{\sqrt6} &0\\ \frac1{\sqrt3} &-\frac1{\sqrt6} &-\frac1{\sqrt2} \end{bmatrix} \end{align*}\]

이 됩니다. (좌변을 계산해보면 정말로 우변이 나옵니다.) 따라서, $A$는 상삼각행렬 $A_2$와 유사합니다.

---

Schur’s lemma를 사용하면 정리 19(b)를 증명할 수 있습니다.

증명[정리 19(b)] : $A$가 $n\times n$ Hermitian 행렬이면 $A$는 unitarilly diagonalizable 합니다.

$A$가 $n\times n$ Hermitian 행렬이라고 가정하겠습니다. 성질 25(Schur’s lemma)에 의해

\[A_{n-1}=UAU^{-1}\]

을 만족시키는 unitary 행렬 $U$와 상삼각행렬 $A_{n-1}$이 존재합니다. $U^{-1}=U^H$임을 활용하면

\[A_{n-1}=UAU^H\]

와 같이 쓸 수도 있습니다. $A_{n-1}$에 conjugate transpose를 취해보면

\[\begin{align*} {A_{n-1}}^H &=\left(UAU^H\right)^H\\ &=\left(U^H\right)^HA^HU^H\\ &=UA^HU^H\\ &=UAU^H\\ &=A_{n-1} \end{align*}\]

입니다. 그러면, $A_{n-1}$은 상삼각행렬이면서 동시에 Hermitian 행렬이므로 $A_{n-1}$이 대각행렬이 될 수밖에 없습니다. 왜냐하면, $i\lt j$인 $i$, $j$에 대하여

\[\begin{align*} \left(A_{n-1}\right)_{ij} &=\left({A_{n-1}}^H\right)_{ij}\\ &=\left(\overline{A_{n-1}}\right)_{ji}\\ &=\overline{\left(A_{n-1}\right)_{ji}}\\ &=\overline 0\\ &=0 \end{align*}\]

이기 때문에 $A_{n-1}$의 오른쪽 윗부분의 성분들이 모두 0이기 때문입니다.

결국

\[A=U^{-1}A_{n-1}U=U^{-1}A_{n-1}\left(U^{-1}\right)^{-1}\]

이고 $U^{-1}$이 unitary 행렬이며, $A_{n-1}$은 대각행렬이므로 $A$는 unitarily diagonalizable합니다. $\square$

---

이로써, 이 포스트의 주요 정리였던 정리 19에 대한 증명을 마쳤습니다.

3 회고

지금까지, 행렬의 직교대각화에 대한 글을 써보았습니다. 사실, 처음 구상했던 바에 비하면 말도안되게 많은 노동이 들어갔다고 생각됩니다. 그러한 수고를 마침내 마무리지을 수 있어서 다행입니다. 다만, 몇번의 퇴고가 더 필요할 것으로 보입니다.

원래 만들었던 TeX파일의 내용만을 옮겨 적어도 되겠지만, 그에 대한 배경설명을 넣으려다보니 글이 길어졌습니다. 또한, 논리적으로 완결성이 있는 글을 작성하고 싶은 욕심에 글을 다지고 다지다보니 글의 분량이 더 길어졌습니다.

수학의 모든 분야가 그럴테지만 선형대수는 그 자체로 상당히 넓은 범위를 가지고 있습니다. 게다가 ‘직교대각화’는 선형대수 줄거리의 후반부에 위치합니다. 그러니 주제가 ‘직교대각화’일 뿐이라고 하더라도, 이에 대해 잘 설명하려면 선형대수 전반에 대해 모두 설명하게 되는 것 같습니다만, 이를 방지하기 위해 무던히 노력했습니다. 이 글은 어디까지나 ‘직교대각화’에 대한 글이기를 바랐고, ‘선형대수 일반’에 대한 글은 아니기를 바랐습니다. 그런 의미에서 다음과 같은 선형대수의 개념들은 등장하게 하지 않도록 했지만 부득이하게 여러번 언급되기는 했습니다. : 벡터공간(vector spaces), 일차독립과 종속(linear independece, independence), 기저(basis), 차원(dimension), 랭크(rank), 열공간과 행공간(column space, row space), null space와 left null space, 정사영(projection), 가우스 소거법 (Gaussian elimination), elementary matrices.

블로그 포스트로서 쓸만한 선형대수 글들은 참 많습니다. 이번 포스트에서 다루지 못한 선형대수의 개념들을 다뤄보는 것도 좋을 것 같습니다. 이 경우, 이 포스트에 대한 보충설명이 될 것입니다만, 이 글과의 연관성을 어떻게 잡아야 할 지 애매한 것이 고민입니다. PCA나 SVD를 정확하게 이해하여 적어보는 것도 좋을 것 같습니다. 이 경우, 이 포스트의 연장선상에서 써나갈 수 있을 것 같지만, 쉬운 일은 아닐 것 같습니다. matrix norm과 Lipschitz constant에 대해서도 쓰고 싶습니다. Fourier series에 대해서도 쓰고 싶습니다만, 이것은 꼭 선형대수와 직접적으로 연관지을 필요는 없을 것입니다. 여하튼, 이것들을 어떻게 구성해나가야 할지에 대해서는 많은 고민이 있습니다.