(Sutton, 4.2, 4.3절) Policy Iteration
더 시간이 지나기 전에 dynamic programming 포스팅을 끝내고 싶은 마음이 생겼다.
다른 주제들도 공부하여 포스팅을 남기고 싶은데 DP를 끝내지 않고 다른 것을 쓰기는 싫기 때문이다. 그러니까 일종의 의무감에서 이 글을 쓰고 있다. 당장 이전부터 PCA와 PLS에 대해 공부하고 싶었고 얼마 전에는 game theory나 control theory에 손을 댈까도 생각했었는데, 오늘은 MPC와 LQR을 배워야 할 필요가 생긴 것이다. 그러니 DP는 빠르게 공부하여 치워버리자.
그리고 사실 글을 쓸 준비가 되어있다고 생각한다. 이전 글을 쓰고 나서 간간이 4.2절을 보았고 어느 정도 이해는 했던 터였다. 책의 내용대로 쭉 따라가볼까.
하지만 글쓰는 것이 쉽지는 않을 것 같다. 사실상 Sutton의 책에 쓰인 것보다 더 간결하고 잘 쓸 수는 없을테니, 글을 쓰고 나서도 나조차도 내 블로그 글을 보기보다는 Sutton의 책을 볼 것 같다. 게다가 당초의 목적은 policy evaluation 증명이었으니 원래의 동기부여는 달성된 셈이다. 그래도 DP를 시작했으니 끝을 보고는 싶다. Sutton의 책을 비슷하게 쓰되 설명을 좀 잘 적어보는 식으로 하자.
4.2 Policy Improvement
policy evaluation을 통해 $v_\pi$ 또는 $q_\pi$를 추정한 것은 더 나은 정책을 찾기 위함이라고 봐도 과언이 아니다. 실제로 Q 함수를 얻어냈다면 그 Q함수에 의거하여 가장 괜찮은 정책, 즉 주어진 $s$에 대하여 $Q(s,a)$가 최대가 되는 $a$를 선택하게 하는 정책을 얻어낼 수 있다. 이것을 greedy policy라고 한다. 물론 Q 함수가 정확하다는 보장이 없기 때문에 greedy policy가 optimal policy라는 것은 아니지만, 그래도 주어진 $Q$에 대한 최선의 정책이겠다.
Sutton의 4.2절은 기존의 정책 $\pi$에 비해 $Q$의 관점에서 더 나은 정책 $\pi’$이 정말로 나은 정책이라는 정리로부터 시작한다. 즉, 상태 $s$에 대하여 정책 $\pi$를 따라갔을 때의 가치 $v_\pi(s)$에 비해, 새로운 행동 $a=\pi’(s)\ne\pi(s)$을 선택한 후 정책 $\pi$를 따라갈 때의 가치가 더 크다면, 새로운 정책 $\pi’$가 기존의 정책 $\pi$보다 낫다는 정리이다.
deterministic policy $\pi$, $\pi'$에 대하여 모든 $s\in\mathcal S$ $$q_\pi(s,\pi'(s))\ge v_\pi(s)\tag{4.7}$$ 라면 $\pi'\ge\pi$이다. 즉, 모든 $s\in\mathcal S$에 대하여 $$v_{\pi'}(s)\ge v_\pi(s)\tag{4.8}$$ 가 성립한다.
이에 대한 증명은 굉장히 straightforward한데, 책에 있는 그대로 따라 써보겠다. 엄밀하게 들어가려면 확률변수들의 급수를 어떻게 정의할지 하는 어려운 문제를 다뤄야 하겠지만 그런 것의 세부는 피하고, 다만 각각의 스텝이 어떻게 정당화될 수 있는지만 보자.
\[\begin{align*} v_\pi(s) \le&q_\pi(s, \pi'(s))\\ =&\mathbb E\left[R_{t+1}+\gamma v_\pi(S_{t+1})|S_t=s, A_t=\pi'(s)\right]\\ =&\mathbb E_{\pi'}\left[R_{t+1}+\gamma v_\pi(S_{t+1})|S_t=s\right]\\ \le&\mathbb E_{\pi'}\left[R_{t+1}+\gamma q_\pi(S_{t+1},\pi'(S_{t+1})\vert S_t=s\right]\\ =&\mathbb E_{\pi'}\left[R_{t+1}+\gamma\mathbb E_{\pi'}\left[R_{t+2}+\gamma v_\pi(S_{t+2})\vert S_{t+1},A_{t+1}=\pi'(S_{t+1})\right] \vert S_t=s\right]\\ =&\mathbb E_{\pi'}\left[R_{t+1}+\gamma R_{t+2}+\gamma^2 v_\pi(S_{t+2})\vert S_t=s\right]\\ \le&\mathbb E_{\pi'}\left[R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\gamma^3 v_\pi(S_{t+3})\vert S_t=s\right]\\ &\vdots\\ \le&\mathbb E_{\pi'}\left[R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\gamma^3 R_{t+4}+\cdots\vert S_t=s\right]\\ =&v_{\pi'}(s) \end{align*}\]첫째줄은 (4.7)을, 둘째줄은 이전 포스트의 (4.3)의 증명과 비슷하게 얻어낼 수 있으며, 셋째줄은 기호의 정의에 의해 당연하다. 넷째줄은 (4.7)을 다시 사용한 것이고 다섯째줄은 둘째줄과 비슷하다. 다섯째줄에 새로 생긴 expectation은 어떤 subscript도 없이 $\mathbb E$로 쓰일 수 있겠지만 $\mathbb E_{\pi’}$라고 쓰여도 무방하다. 그리고 $\mathbb E_{\pi’}$으로 적혔기 때문에 다음 여섯번째 식이 성립하게 된다. 이제, 셋째줄에서 여섯째줄로 변하는 과정을 한 번 더 반복한다고 하면 일곱번째 식이 되고, 이것을 무한히 반복한다고 생각하면 여덟번째 식이 된다. 그리고 급수의 정의를 생각하면 아홉번째 식이 이와 같고, 그것은 곧 열번째 식의 $v_{\pi’}(s)$의 정의와 정확히 일치한다. 이렇게 하여 policy improvement theorem이 증명되었다. $\square$
정책개선정리는 정책 $\pi$가 주어져 있을 때 이보다 더 좋은 정책 $\pi’$을 만들어낼 여지를 마련한다. 그러면, 이 정리를 최대한으로 활용하여 만들어낼 수 있는 새로운 정책 $\pi’$이 있다. 이것은 부등식 (4.7)의 좌변이 최대한으로 되는 경우이다. 이 정책을 greedy policy라고 부른다.
greedy policy $\pi’$는 통상 모든 $s$에 대하여
\[\begin{align*} \pi'(s) &=\text{arg}\max_a q_\pi(s,a)\\ &=\text{arg}\max_a\mathbb E\left[R_{t+1}+\gamma v_\pi(S_{t+1})\vert S_t=s,A_t=a\right]\tag{4.9}\\ &=\text{arg}\max_a\sum_{s',r}p(s',r\vert s,a)\left[r+\gamma v_\pi(s')\right] \end{align*}\]인 정책 $\pi’$으로 정의한다. 즉, 여러 $a$들 중 $q_\pi(s,a)$가 최댓값을 가지는 $a$를 $\pi’(s)$로 정의하는 것이다. 최댓값을 가지는 $a$는 유일하지 않을 수 있으니 그러한 $a$들 중 하나를 $\pi’(a)$로 정의한다고 보면 되겠다.
이러한 $\pi’$는 deterministic policy이다. 반면, $\pi’$를 stochastic policy로서 다음과 같이 정의해도 되겠다. 주어진 $s$에 대해서 $q$값이 가장 큰 action(들)을 다 더해서 1이 되도록 확률을 주고 나머지 action에 대해서는 모두 0으로 주는 것이다. 예를 들어, $A_s=\{a’\in A:q_\pi(s,a’)=\max_{a\in\mathcal A}q_\pi(s,a)\}$ 로 두고
\[\begin{align*} \pi'(a|s) = \begin{cases} \frac1{\left|A_s\right|}&a\in A_s\\ 0 &a\notin A_s\\ \end{cases} \end{align*}\]와 같이 정의할 수 있다.
정책 $\pi$에 대하여 $\pi'\ge\pi$를 만족시키는 새로운 정책 $\pi'$를 선택하는 것을 정책개선 이라고 부른다. greedy policy는 정책개선 중 가장 적극적인 정책개선이다.
주어진 정책 $\pi$에 대한 greedy policy $\pi’$가 더이상 개선되지 않고 이전과 그 가치가 같다고, 즉 $v_{\pi’}=v_\pi$를 만족한다고 하자. 그러면 (4.9)에 의해
\[\begin{align*} v_{\pi'}(s) &=q_{\pi'}(s,\pi'(s))\\ &=q_\pi(s,\pi'(s))\\ &=\max_a q_\pi(s,a)\\ &=\max_a\sum_{s',r}p(s',r\vert s,a)\left[r+\gamma v_\pi(s')\right]\\ &=\max_a\sum_{s',r}p(s',r\vert s,a)\left[r+\gamma v_{\pi'}(s')\right] \end{align*}\]이다. (이것은 Sutton 책에 써진 것을 더 세부적으로 써본 것이다.) 첫번째 줄은 기호의 정의에 의해 당연히 성립한다. 두번째 줄은 $v_{\pi’}=v_\pi$로부터 $q_{\pi’}=q_\pi$를 유도할 수 있기 때문에 그렇다(Bellman equation). 세번째와 네번째 줄은 (4.9)에서부터 나왔고, 마지막 다섯번째 줄은 $v_{\pi’}=v_\pi$이다.
그러면 위 식은 Bellman optimal equation (3.18)과 같다. 특별한 경우가 아닌 이상 연립방정식 Bellman optimal equation의 해가 유일할 것이므로, 이 정책 $\pi’$은 optimal policy라고 말할 수 있다.
4.3 Policy Iteration
어떤 $\pi$에 대하여 policy evaluation과 policy improvement를 반복할 수 있다.
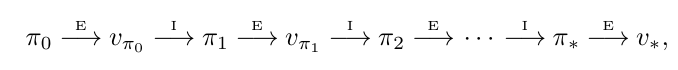
정책 평가와 정책 개선을 반복하는 것인데 이것을 policy iteration이라고 한다. 정책개선시 deterministic한 policy를 택한다고 가정하면, finite MDP의 deterministic policy의 개수는 유일하고, optimal policy 또한 deterministic하다고 가정할 수 있으므로 policy iteration는 언젠가 끝난다. 즉, 어느 순간 ($K$번째에) 최적정책 $\pi_\ast$에 도달하며 그때의 정책은 $v_{\pi_K}=v_{\pi_{K-1}}$를 만족할 것이다.
정책평가시 가치함수의 초깃값을 설정해야 했다. 그 초깃값이 어떻건 항상 $v_\pi$로 수렴한다는 것은 이전 포스트에서 증명했었다. 하지만 이 경우에는 초깃값을 직전 가치함수로 두면 수렴 속도에 있어서 유리하다는 것이 언급되고 있다. 즉, $\pi_i\stackrel{E}{\longrightarrow}v_{\pi_i}$의 정책평가를 진행할 때 가치함수의 초깃값을 $v_{i-1}$로 놓으면 수렴이 빨라진다는 것이다. 이것을 warm start라고도 부른다.
아래는 Sutton 책에 실린 pseudocode이다. warm start 버전인 것을 확인할 수 있다.

4.3.1 코드 구현
이전 포스트에서 다음과 같은 grid world에서 equiprobable policy에 대한 가치함수를 계산해봤었다.
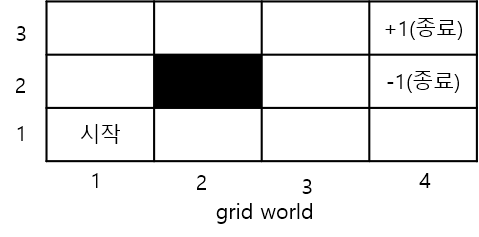
이번에는 policy iteration을 통해 최적 정책을 찾아보려 한다.
4.5장에는 policy evaluation의 빈도에 따라 syncronous PI와 syncronous PI를 구분하고 있는데 이것을 in_place 인자로 두었다. (asyncronous PI : in_place=True)
또, 정책평가는 정책 평가의 과정 (한 번의 업데이트, sweep)이 여러 번 반복되는데 모든 sweep 이후에 policy improvement로 넘어갈지 아니면 한 번의 sweep마다 policy improvement로 넘어갈지 결정하는 인자로 max_sweep을 도입했다. (모든 sweep 이후에 PI로 넘어감 : max_sweep=True)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
from env import GridWorld
env = GridWorld()
V_init = {s: 0.0 for s in env.get_states()} # Value function
policy_init = {s: 'R' for s in env.get_states()} # Initial policy
def policy_evaluation(policy, V, in_place, max_sweep, threshold=0.001):
"""
Policy Evaluation
Args:
in_place (bool) : True = asyncronous update, False : syncronous update
max_sweep (bool) : True = sweeps until convergence, False : one sweep
threshold (float) : convergence threshold
"""
while True:
if not in_place:
V_old = V.copy()
delta = 0
for state in env.get_states():
if env.is_terminal(state):
continue
action = policy[state]
next_state = env.get_next_state(state, action)
reward = env.get_reward(state, action)
if in_place:
# Asynchronous: 즉시 업데이트 (현재 V 사용)
v_old = V[state]
V[state] = reward + env.gamma * V[next_state]
else:
# Synchronous: old V 사용해서 new V 계산
v_old = V_old[state]
V[state] = reward + env.gamma * V_old[next_state]
delta = max(delta, abs(v_old - V[state]))
# 종료 조건
if max_sweep:
if delta < threshold:
break
else:
break
return V
def policy_improvement(policy, V):
"""Policy Improvement"""
is_convergent = True
for state in env.get_states():
if env.is_terminal(state):
continue
old_action = policy[state]
# 모든 행동에 대해 Q값 계산
action_values = {}
for action in env.actions:
next_state = env.get_next_state(state, action)
reward = env.get_reward(state, action)
action_values[action] = reward + env.gamma * V[next_state]
# 최선의 행동 선택
policy[state] = max(action_values, key=action_values.get)
if old_action != policy[state]:
is_convergent = False
return policy, is_convergent
def print_results(policy, V):
"""결과 출력"""
print("\nValue Function:")
for r in range(env.rows - 1, -1, -1): # 2, 1, 0 순서 (상하반전)
row_values = []
for c in range(env.cols):
if (r, c) == env.wall:
row_values.append(" WALL ")
else:
row_values.append(f"{V[(r,c)]:6.2f}")
print(" ".join(row_values))
print("Policy:")
for r in range(env.rows - 1, -1, -1): # 2, 1, 0 순서 (상하반전)
row_policy = []
for c in range(env.cols):
if (r, c) == env.wall:
row_policy.append(" W ")
elif env.is_terminal((r, c)):
row_policy.append(" T ")
else:
row_policy.append(f" {policy[(r,c)]} ")
print(" ".join(row_policy))
def policy_iteration(policy, V, in_place, max_sweep):
"""Policy Iteration"""
iteration = 0
print(f"\n{'='*60}")
print(f"🎯 POLICY ITERATION │ {"Asyncronous" if in_place else "Syncronous"} + {"Full sweep" if max_sweep else "single sweep"}")
print(f"{'='*60}\n")
while True:
iteration += 1
# Iteration은 간소화
print(f"\n[Iteration {iteration}]")
V = policy_evaluation(policy, V, in_place=in_place, max_sweep=max_sweep)
policy, is_convergent = policy_improvement(policy, V)
print_results(policy, V)
if is_convergent:
print(f"\n✅ Policy converged after {iteration} iterations!")
break
4.3.2 구현 결과
옵션이 두 개이니 총 네 번의 실험을 해볼 수 있다. 그때마다의 결과를 표로 정리하면 다음과 같다.
in_place=True |
in_place=False |
|
|---|---|---|
max_sweep=True |
1번만에 수렴 | 4번만에 수렴 |
max_sweep=False |
1번만에 수렴 | 1번만에 수렴 |
즉, 4.3의 본문에서 설명한 기본적인 policy iteration 방식은 in_place=False, max_sweep=True인데 이 경우에는 4번의 iteration을 거쳐서 정책이 수렴했다.
반면, in_place=True로 두어 asyncronous 방식을 취하거나 아니면 sweep마다 policy improvement를 시행한 경우에는 한 번만에 정책이 수렴했다.
아래는 세부 결과이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
# syncronous, full sweep
policy_iteration(policy_init, V_init, in_place=True, max_sweep=True)
============================================================
🎯 POLICY ITERATION │ Asyncronous + Full sweep
============================================================
[Iteration 1]
Value Function:
0.62 0.80 1.00 0.00
-0.99 WALL -1.00 0.00
-0.99 -0.99 -0.99 -0.99
Policy:
R R R T
U W U T
U U D D
[Iteration 2]
Value Function:
0.62 0.80 1.00 0.00
0.46 WALL 0.80 0.00
0.31 -0.99 -0.99 -0.99
Policy:
R R R T
U W U T
U L U D
[Iteration 3]
Value Function:
0.62 0.80 1.00 0.00
0.46 WALL 0.80 0.00
0.31 0.18 0.62 -0.99
Policy:
R R R T
U W U T
U R U L
[Iteration 4]
Value Function:
0.62 0.80 1.00 0.00
0.46 WALL 0.80 0.00
0.31 0.46 0.62 0.46
Policy:
R R R T
U W U T
U R U L
✅ Policy converged after 4 iterations!
# asyncronous, full sweep
policy_iteration(policy_init, V_init, in_place=False, max_sweep=True)
============================================================
🎯 POLICY ITERATION │ Syncronous + Full sweep
============================================================
[Iteration 1]
Value Function:
0.62 0.80 1.00 0.00
0.46 WALL 0.80 0.00
0.31 0.46 0.62 0.46
Policy:
R R R T
U W U T
U R U L
✅ Policy converged after 1 iterations!
# syncronous, single sweep
policy_iteration(policy_init, V_init, in_place=True, max_sweep=False)
============================================================
🎯 POLICY ITERATION │ Asyncronous + single sweep
============================================================
[Iteration 1]
Value Function:
0.62 0.80 1.00 0.00
0.46 WALL 0.80 0.00
0.31 0.46 0.62 0.46
Policy:
R R R T
U W U T
U R U L
✅ Policy converged after 1 iterations!
# asyncronous, single sweep
policy_iteration(policy_init, V_init, in_place=False, max_sweep=False)
============================================================
🎯 POLICY ITERATION │ Syncronous + single sweep
============================================================
[Iteration 1]
Value Function:
0.62 0.80 1.00 0.00
0.46 WALL 0.80 0.00
0.31 0.46 0.62 0.46
Policy:
R R R T
U W U T
U R U L
✅ Policy converged after 1 iterations!
댓글남기기