(Sutton, 4.1절) Policy Evaluation
이전 포스트에 이어 Sutton의 책을 읽어가보자.
늘 그렇듯 책에 생략된 내용에 대해서는 자료를 찾거나 직접 계산 또는 증명해서 채워나갈 것이다. dynamic programming은, 이 책에서는 가장 기본적인 강화학습 알고리즘으로 소개된다. 환경모델이 완전히 주어진 상태에서 쓸 수 있는 가장 기본적인 알고리즘이라고 할만하다.
공부를 하면 할수록 강화학습의 fundamental이 되는 이 계산들이나 정리들이 꽤 만만치 않음을 느낀다. 이런 어려움은 나만 겪는 것이 아니라고도 생각해본다. 사람들이 때로, 아주 간단한 식에도 나처럼 심각하게 고민한 것을 몇 번 봤다.
Sutton의 3장은 꽤 책의 내용과 비슷하게 썼다. 하지만 내가 관심있는 수학적인 부분은 책에 자세하게 설명되지 않고 있기 때문에 책 외의 내용이 많이 적힐 예정이다. 식번호는 책의 것을 그대로 따랐으나, 절은 다르게 썼다.
이 포스트에서 꼭 다루고자 하는 것은 Bellman operator와 contraction principle로 policy evaluation이 유효한 것임을 증명하는 것이다. 이에 관해서는 이미 Ishwin Rao나 Carl Fredricksson이 잘 써놨는데 아마 조금씩 참고할 것 같다.
정확한 증명을 위해 계속 파다보니 operator norm에 대해서도 이야기해야 했다. 그런데, 가만히 보면 contraction principle이나 operator norm 모두 내 석사논문에서 다뤘던 주제들이다. 사실 수학 전체로 보면 조금 기본적인 내용들을 내 부끄러운 석사논문에 넣었던 것인데 그때 공부했던 것이 직접적인 도움이 되었다. 어떻게 보면 policy evaluation은 Bellman operator의 Lipschitz constant가 1보다 작다는 사실을 이용하고 있다.
4. Dynamic Programming
4장의 맨 처음에 나오는 것은 Bellman optimal equation이다. 이 장에서는 DP를 이용해 optimal policy를 얻어내는 과정을 설명하고 있으니 optimal policy에 관한 다음 식이 중요한 것은 당연하다. optimal value $v_\ast$, $q_\ast$에 대한 optimal equation들을 다시 써보면 다음과 같다.
\[\begin{align*} v_\ast(s) &=\max_a\mathbb E\left[R_{t+1}+\gamma v_\ast(S_{t+1})|S_t=s, A_t=a\right]\\ &=\max_a\sum_{s',r}p(s',r|s,a)\left[r+\gamma v_\ast(s')\right]\tag{4.1}\\ q_\ast(s,a) &=\mathbb E\left[R_{t+1}+\gamma\max_{a'}q_\ast(S_{t+1},a')|S_t=s, A_t=a\right]\\ &=\sum_{s',r}p(s',r|s,a)\left[r+\gamma\max_{a'}q_\ast(s',a')\right]\tag{4.2} \end{align*}\]4.1 Policy Evaluation (Prediction)
4장 1절에서는 policy evaluation에 대해 다룬다. 그리고 이것이 이 포스트의 주제이다.
4.1.1 Bellman equation revisited
$v_\pi$에 대한 Bellman equation은 이전 포스트에서 썼지만 다시 적어보자.
\[\begin{align*} v_\pi(s) &=\mathbb E_\pi\left[G_t|S_t=s\right]\\ &=\mathbb E_\pi\left[R_{t+1}+\gamma G_{t+1}|S_t=s\right]\\ &=\mathbb E_\pi\left[R_{t+1}+\gamma v_\pi(S_{t+1})|S_t=s\right]\tag{4.3}\\ &=\sum_a\pi(a|s)\sum_{s',r}p(s',r|s,a)\left[r+\gamma v_\pi(s')\right]\tag{4.4} \end{align*}\]첫번째 줄과 두번째줄이 같다는 것, 그리고 그것이 네번째 줄과 같다는 것은 이전 포스트에서 증명했고, 그것을 Bellman equation이라고 했었다. 그러나 세번째 줄은 지금까지 없었던 식이다. 그래, 의미상으로는 당연히 그럴 것 같은데 왜 그런 지는 그렇게까지 쉽게 설명되지 않는다. 그러니, 세번째 줄로부터 시작하여 네번째 줄로 도출되는 계산을 해보려 한다.
$\pi$와 $p$의 정의, Markov property, 기댓값의 정의 등에 의해 다음과 같이 계산된다.
\[\begin{align*} &\mathbb E_\pi\left[R_{t+1}+\gamma v_\pi(S_{t+1})|S_t=s\right]\\ =&\sum_a\pi(a|s)\mathbb E\left[R_{t+1}+\gamma v_\pi(S_{t+1})|S_t=s,A_t=a\right]\\ =&\sum_a\pi(a|s)\sum_{s',r}p(s',r|s,a)\mathbb E_\pi\left[R_{t+1}+\gamma v_\pi(S_{t+1})|S_t=s,A_t=a,R_{t+1}=r,S_{t+1}=s'\right]\\ =&\sum_a\pi(a|s)\sum_{s',r}p(s',r|s,a)\mathbb E_\pi\left[r+\gamma v_\pi(S_{t+1})|S_{t+1}=s'\right]\\ =&\sum_a\pi(a|s)\sum_{s',r}p(s',r|s,a)\mathbb E_\pi\left[r+\gamma v_\pi(s')\right]\\ \end{align*}\]더 나아가기 전에 Q함수에 대한 비슷한 다음 식도 증명해보자. 이것은 나중에 SARSA와 Q-learning을 위해 필요하다. 다음과 같은 식이다.
\[\begin{align*} q_\pi(s,a) &=\mathbb E_\pi\left[G_t|S_t=s,A_t=a\right]\\ &=\mathbb E_\pi\left[R_{t+1}+\gamma G_{t+1}|S_t=s,A_t=a\right]\\ &=\mathbb E_\pi\left[R_{t+1}+\gamma q_\pi(S_{t+1},A_{t+1})|S_t=s, A_t=a\right]\tag{$4.3*$}\\ &=\sum_{s',r}p(s',r|s,a) \left(r+\gamma\sum_{a'}\pi(a'|s')q_\pi(s',a')\right)\tag{$4.4*$} \end{align*}\]이번에도 첫번째 식과 두번째 식, 그리고 네번째 식이 같다는 것은 이전 포스트에서 증명했다. 세번째 식을 전개했을 때 네번째 식이 된다는 것을 증명하기만 하면 되는데 다음과 같다.
\[\begin{align*} &\mathbb E_\pi\left[R_{t+1}+\gamma q_\pi(S_{t+1},A_{t+1})|S_t=s, A_t=a\right]\\ =&\sum_{s',r}p(s',r|s,a)\mathbb E_\pi\left[R_{t+1}+\gamma q_\pi(S_{t+1},A_{t+1})|S_t=s, A_t=a,R_{t+1}=r,S_{t+1}=s'\right]\\ =&\sum_{s',r}p(s',r|s,a)\left(r+\gamma\mathbb E_\pi\left[q_\pi(S_{t+1},A_{t+1})|S_t=s, A_t=a,R_{t+1}=r,S_{t+1}=s'\right]\right)\\ =&\sum_{s',r}p(s',r|s,a)\left(r+\gamma\sum_{a'}\pi(a'|s')\mathbb E_\pi\left[q_\pi(S_{t+1},A_{t+1})|S_t=s, A_t=a,R_{t+1}=r,S_{t+1}=s',A_{t+1}=a'\right]\right)\\ =&\sum_{s',r}p(s',r|s,a)\left(r+\gamma\sum_{a'}\pi(a'|s')q_\pi(s',a')\right)\\ \end{align*}\]4.1.2 policy evaluation
책의 4.1절에서 다루는 것은, 주어진 정책 $\pi$에 대하여 이에 대한 가치함수 $v_\pi$를 얻어내는 것이다. 즉 정책을 평가하는(policy evaluation, prediction problem) 것으로서 DP를 포함한 모든 강화학습에서의 중요한 두 과정 중 하나이다.
가치함수를 얻어내는 방식은 식 (4.4)를
\[v_{k+1}(s)=\sum_a\pi(a|s)\sum_{s',r}p(s',r|s,a)\left[r+\gamma v_k(s')\right]\tag{4.5}\]와 같이 변형해 가치함수들의 수열 $v_0, v_1, v_2, \cdots$을 만들어나가는 것이다. $v_0$가 임의의 가치함수(e.g. $v_0\equiv0$)이고 $v_\pi$가 존재한다는 조건 하에 수열 $\{v_i\}$가 $v_\pi$로 수렴하는 것이 알려져 있고 이것을 Sutton은 증명하지 않고 넘어갔다. 이 포스트에서 이를 증명해보려 한다. 정확하게는 다음과 같다.
$0\lt\gamma\lt1$인 finite MDP $\mathscr D\left(\mathcal S, \mathcal A, p, \gamma\right)$의 한 정책을 $\pi$라고 하자. 임의의 가치함수 $v_0:\mathcal S\to\mathbb R$에 대하여 가치함수의 수열 $\lbrace v_k\rbrace_{k=0}^\infty$를 식 (4.5)와 같이 정의하면 $k\to\infty$일 때 $v_k$는 $v_\pi$로 수렴한다.
\[\lim_{k\to\infty}v_k=v_\pi\]
수열의 수렴을 이야기하려면 함수 $v_k$가 속해있는 공간을 정의해야 할텐데, 여기서는 함수공간 $\mathcal V=\{v:\mathcal S\to\mathbb R\}$에 대하여 normed space $\left(\mathcal V,\vert\vert\cdot\vert\vert_\infty\right)$을 생각하는 것이다. Sutton은 어느 순간엔가 $v_K=v_{K+1}=\cdots$이 되어 수렴한다고 적고 있는데, 위에 쓴 수렴은 Sutton이 말한 수렴의 의미를 포함한다.
4.1.3 Bellman operator
먼저 할 것은 식 (4.4) 버전의 Bellman equation을 Bellman operator으로 표현하는 것이다. 기본적으로 Carl Fredricksson의 자료를 따라갔다.
많은 계산들, 특히 marginalization이 포함되어 있으므로 천천히 계산하기 위해 일단 두 값 $A$, $B$로 분리하면 식 (4.4)에서
\[\begin{align*} v_\pi(s) &=\sum_a\pi(a|s)\sum_{s',r}p(s',r|s,a)\left[r+\gamma v_\pi(s')\right]\\ &=\sum_{a,s',r}r\pi(a|s)p(s',r|s,a)+\gamma\sum_{a,s',r}v_\pi(s')\pi(a|s)p(s',r|s,a)\\ &=A+\gamma B \end{align*}\]이다. 먼저 $A$를 계산하면
\[\begin{align*} A&=\sum_{a,s',r}r\pi(a|s)p(s',r|s,a)\\ &=\sum_{a,s',r}r\frac{P\left(S_t=s,A_t=a\right)}{P\left(S_t=s\right)}\times \frac{P\left(S_t=s,A_t=a,S_{t+1}=s',R_{t+1}=r\right)}{P\left(S_t=s,A_t=a\right)}\\ &=\sum_r r\sum_{a,s'}\frac{P\left(S_t=s,A_t=a,S_{t+1}=s',R_{t+1}=r\right)}{P\left(S_t=s\right)}\\ &=\sum_r r\frac{P\left(S_t=s,R_{t+1}=r\right)}{P\left(S_t=s\right)}\\ &=\sum_r r{P\left(R_{t+1}=r|S_t=s\right)}\\ &=\mathbb E_\pi\left[R_{t+1}|S_t=s\right]\\ &=r_\pi(s) \end{align*}\]이다. 두번째 줄은 두 표현 $\pi(\cdot|\cdot)$, $p(\cdot,\cdot|\cdot,\cdot)$ 정의, 세번째 줄은 통분, 네번째 줄은 두 변수에 $a$, $s’$에 대한 marginalization, 다섯번째 줄과 여섯번째 줄은 각각 조건부확률과 조건부기댓값의 정의에 의해 계산되었다. 마지막 줄은 새롭게 $r_\pi$라는 함수를 정의한 것이다.
다음으로 $B$를 계산하는데 통분과 같은 과정은 빠르게 넘어가면서 계산해보려 한다. 계산해보면
\[\begin{align*} B &=\sum_{a,s',r}v_\pi(s')\pi(a|s)p(s',r|s,a)\\ &=\sum_{s'}v_\pi(s')\sum_{a,r}\frac{P\left(S_t=s,A_t=a,S_{t+1}=s',R_{t+1}=r\right)}{P\left(S_t=s\right)}\\ &=\sum_{s'}v_\pi(s')\frac{P\left(S_t=s,S_{t+1}=s'\right)}{P\left(S_t=s\right)}\\ &=\sum_{s'}v_\pi(s')P\left(S_{t+1}=s'|S_t=s\right) \end{align*}\]와 같다. 두번째 줄은 기호의 정의와 통분, 세번째 줄은 marginalization, 네번째 줄은 조건부확률의 정의에 의해 계산되었다. 마지막 식은 $\mathbb E\left[v_\pi(S_{t+1})|S_t=s\right]$로도 쓸 수 있지만 위의 계산결과까지만 사용할 것이다. 계산한 $A$와 $B$를 가지고 Bellman equation을 다시 쓰면
\[v_\pi(s)=r_\pi(s)+\gamma\sum_{s'}v_\pi(s')P\left(S_{t+1}=s'|S_t=s\right)\]이 된다. 이전 포스트에도 언급했고, 책의 4장에도 다시 강조되지만 Bellman equation의 본질은 연립방정식, 그것도 선형(affine)연립방정식이다. state space $\mathcal S$를 $\mathcal S=\{s^1,\cdots,s^n\}$으로 두고 위 식을 다시 쓰면 모든 $i,j$에 대하여 ($1\le i,j\le n)$
\[v_\pi(s^j)=r_\pi(s^j)+\gamma\sum_{i=1}^nv_\pi(s^i)P\left(S_{t+1}=s^i|S_t=s^j\right)\]이 성립한다. 선형(affine)방정식이니, 벡터와 행렬로 표현하면 가장 적절하다. 행렬 $P\in\mathbb R^{n\times n}$를
\[P= \begin{bmatrix} P\left(S_{t+1}=s^1|S_t=s^1\right)&\cdots&P\left(S_{t+1}=s^n|S_t=s^1\right)\\ \vdots&\ddots&\vdots\\ P\left(S_{t+1}=s^1|S_t=s^n\right)&\cdots&P\left(S_{t+1}=s^n|S_t=s^n\right) \end{bmatrix}\]로 정의하고 벡터 $v_\pi,r_\pi\in\mathbb R^n$을
\[v_\pi= \begin{bmatrix} v_\pi(s^1)\\ \vdots\\ v_\pi(s^n) \end{bmatrix} ,\quad r_\pi= \begin{bmatrix} r_\pi(s^1)\\ \vdots\\ r_\pi(s^n) \end{bmatrix}\]으로 두면 Bellman equation은
\[v_\pi=r_\pi+\gamma Pv_\pi\]가 된다. (즉, $v_\pi$는 가치함수로서의 함수이기도 하지만, 벡터이기도 하다. 문맥에 따라 두 의미가 혼동되지 않는다.) 이런 관점에서 Bellman operator $\mathcal T^\pi$를 다음과 같이 정의할 수 있다.
가치함수 $v:\mathcal S\to\mathbb R$에 대하여 $\mathcal T^\pi v$를
\[\mathcal T^\pi v=r_\pi+\gamma Pv\]로 정의한다. 다시 말해, 모든 $s\in\mathcal S$에 대하여
\[\begin{align*} \left(\mathcal T^\pi v\right)(s) &=r_\pi(s)+\gamma(Pv)(s)\\ &=\sum_a\pi(a|s)\sum_{s',r}p(s',r|s,a)\left[r+\gamma v(s')\right] \end{align*}\]이다.
그러면 Bellman equation도 간단히
\[v_\pi=\mathcal T^\pi v_\pi\tag{$\ast$}\]로 쓰일 수 있다. 그리고 policy evaluation 식 (4.5)도
\[v_{k+1}=\mathcal T^\pi v_k\]로 표현될 수 있다.
4.1.4 the contraction principle
이제 순수하게 수학적인 정리가 나올 차례이다. baby rudin (3ed)의 9.22, 9.23에 다음과 같은 내용이 있다. 먼저 9.22는 contraction에 대한 정의이다.
(9.22 정의) 거리공간 $(X,d)$에 대하여 함수 $\phi:X\to X$가 어떤 실수 $0\le c\lt1$에 대해 모든 $x,y\in X$에 대하여
\[d\left(\phi(x),\phi(y)\right)\le cd(x,y)\]를 만족시키면 $\phi$를 $X$의 contraction이라고 부른다.
contraction principle은 9.23에 해당하는 다음의 정리이다.
(9.23 정리) 만약 $X$가 complete space이고 $\phi$가 $X$의 contraction이면 $\phi(x^\ast)=x^\ast$를 만족시키는 $x^\ast$가 존재하고 그러한 $x^\ast$는 유일하다.
어떤 거리공간이 complete하다는 것은 코시수열이 수렴한다는 것을 말한다. 이 공간에서 거리가 점점 줄어드는 함수가 있으면, 그 함수는 고정점(fixed point)이 반드시 존재한다는 아주 강력하고 재미있는 정리이다. 이것은 Banach fixed point theorem이라는 이름도 가지고 있다.
증명은 비교적 쉽다. 그리고 그 fixed point를 찾아가는 과정이, 꼭 policy evaluation과도 비슷하다. 즉, 아무 점 $x_0\in X$를 잡더라도 $\phi$를 계속해서 취해나가면 일정한 점 $x^\ast$에 이른다는 것이다.
임의의 점 $x_0\in X$에서 출발하여 수열 $\{x_n\}_{n=0}^\infty$를
\[x_{n+1}=\phi(x_n)\]로 반복적으로 정의하자. 그러면
\[\begin{align*} d(x_n,x_{n+1}) =&d\left(\phi(x_{n-1}),\phi(x_n)\right)\\ \le&cd(x_{n-1},x_n)\\ &\vdots\\ \le&c^nd(x_0,x_1) \end{align*}\]가 된다. 그러면 $m\gt n$일 때
\[\begin{align*} d(x_n,x_m) &\le d(x_n,x_{n+1})+d(x_{n+1},x_{n+2})+\cdots+d(x_{m-1},x_m)\\ &\le c^nd(x_0,x_1)+c^{n+1}d(x_0,x_1)+\cdots+c^{m-1}d(x_0,x_1)\\ &=\frac{c^n(1-c^{m-n})}{1-c}d(x_0,x_1)\\ &\le\frac{c^n}{1-c}d(x_0,x_1)\\ \end{align*}\]이다. 첫번째 줄은 삼각부등식, 두번째 줄은 바로 위의 부등식, 세번째 줄은 등비수열의 합 공식을 사용했고 네번째 줄은 당연하다. 그러면 임의의 양수 $\epsilon\gt0$에 대하여
\[\frac{c^N}{1-c}d(x_0,x_1)\lt\epsilon\]을 만족시키는 자연수 $N$가 존재한다. $m\gt n\gt N$이면
\[d(x_n,x_m) \le\frac{c^n}{1-c}d(x_0,x_1) \le\frac{c^N}{1-c}d(x_0,x_1)\lt\epsilon\]이므로 수열 $\{x_n\}$은 코시수열이다. 그런데 $X$가 complete space이므로 이 수열은 어떤 점 $x^\ast$엔가에 수렴하게 된다. 이때, contraction이 연속함수라는 건 당연하므로
\[\phi(x^\ast) =\phi\left(\lim_{n\to\infty}x_n\right) =\lim_{n\to\infty}\phi(x_n) =\lim_{n\to\infty}x_{n+1} =x^\ast.\]이다. 즉, $x^\ast$는 $\phi$의 고정점(fixed point)이다.
또한 만약 고정점이 두 개 $x^\ast$, $y^\ast$ 존재한다면
\[d(x^\ast,y^\ast)=d\left(\phi(x^\ast),\phi(y^\ast)\right)\le cd(x^\ast,y^\ast)\]이 되어 $(1-c)d(x^\ast,y^\ast)\le0$, $d(x^\ast,y^\ast)=0$이 되어 $x^\ast=y^\ast$가 된다. 즉 고정점 $x^\ast$는 유일하다. $\square$
4.1.5 operator norm : $||P||\le1$
policy evaluation 증명의 완성을 위해서는 $P$의 operator norm $||P||$가 1보다 작거나 같다는 사실이 필요하다. 여기서 말하는 operator norm이란 $P$를 $\left(\mathbb R^n, \lvert\lvert\cdot\rvert\rvert_\infty\right)$ 에서 $\left(\mathbb R^n, \lvert\lvert\cdot\rvert\rvert_\infty\right)$ 로 가는 operator로 보았을 때의 operator norm을 말한다. 이것은 matrix norm이라고도 한다.
operator norm의 여러가지 정의 중
\[\lVert A\rVert=\sup\{\lVert Av\rVert:\lVert v\rVert\le1\}\]을 사용하자. 4.3에서 정의한 행렬 $P$는 각 행의 합이 1이다. 즉,
\[P=[p_{ij}]_{n\times n} = \begin{bmatrix} P\left(S_{t+1}=s^1|S_t=s^1\right)&\cdots&P\left(S_{t+1}=s^n|S_t=s^1\right)\\ \vdots&\ddots&\vdots\\ P\left(S_{t+1}=s^1|S_t=s^n\right)&\cdots&P\left(S_{t+1}=s^n|S_t=s^n\right) \end{bmatrix}\]에서 $\sum_jp_{ij}=1$이다. ($i=1,\cdots,n$) 그러면
\[\left|\left|p_{i1}v_1+\cdots+p_{in}v_n\right|\right|_\infty \le p_{i1}\Vert v\Vert_\infty+\cdots+p_{in}\Vert v\Vert_\infty =\Vert v\Vert_\infty\]이므로
\[\left|\left|Pv\right|\right|_\infty =\max\{\left|\left|p_{i1}v_1+\cdots+p_{in}v_n\right|\right|_\infty:i=1,\cdots,n\} \le\Vert v\Vert_\infty\]이고, 따라서
\[\Vert P\Vert =\sup\{\Vert Pv\Vert_\infty:\Vert v\Vert_\infty\le1\} \le1\]이다.
4.1.6 proof (policy evaluation)
이제 policy evaluation의 증명이 가능하다. 두 벡터 $v,w\in\mathbb R^n$에 대하여
\[\begin{align*} \left|\left|T^\pi v - T^\pi w\right|\right|_\infty &=\left|\left|(r_\pi+\gamma Pv) - (r_\pi+\gamma Pw)\right|\right|_\infty\\ &=\gamma\left|\left|P(v-w)\right|\right|_\infty\\ &\le\gamma\lvert\lvert P\rvert\rvert\cdot\lvert\lvert v-w\rvert\rvert_\infty\\ &\le\gamma||v-w||_\infty\\ \end{align*}\]이다. 첫번째 줄은 Bellman operator의 정의, 두번째 줄은 $P$의 선형성과 norm의 성질, 세번째 줄은 operator norm의 성질, 네번째 줄은 $\lvert\lvert P\rvert\rvert\le1$이 쓰였다. 이것을 다시 쓰면
\[d\left(\mathcal T^\pi v,\mathcal T^\pi w\right) \le \gamma d(v,w)\]이 된다. $0\lt\gamma\lt1$ 이므로 $\mathcal T^\pi$는 $\left(\mathbb R^n, \lvert\lvert\cdot\rvert\rvert_\infty\right)$ 에서의 contraction이다. 그러면 contraction principle에 의해
\[\mathcal T^\pi v^\ast=v^\ast\]인 $v^\ast\in\mathbb R^n$이 유일하게 하나 존재하고 식 (4.5)로 정의된 수열 $\{v_k\}$에 대하여 $v_k\to v^\ast$이다. 즉 Bellman equation $(\ast)$이 유일한 해 $v^\ast$를 가진다. 따라서 $v^\ast=v_\pi$이다. 그러면
\[\lim_{k\to\infty}v_k=v^\ast=v_\pi\]가 성립한다. $\square$
이로써 policy evaluation을 통해 $\pi$에 대한 가치함수 $v_\pi$를 반복적인 방식으로 수렴해나갈 수 있음을 증명했다.
책에 적혀진 내용들을 조금 더 써볼까.
Sutton은 PE를 구현하는 방법으로 두 가지 방법(two-array, in-place)을 제시한다. two-array 방법에서는 말그대로 두 개의 array를 사용하는데 하나는 각 $s$에 대한 old values $v_k(s)$를 기록하는 array로 다른 하나는 각 new values $v_{k+1}(s)$를 기록하는 array이다. old array를 사용하여 new array를 만든 이후에는 new array를 old array로 생각하고 이전에 old array였던 것을 $v_{k+1}(s)$를 기록하는 new array로 두어 계속한다. in-place 방법에서는 하나의 array만을 사용한다. $s^i$에 대한 $v_k(s^i)$를 먼저 덮어씌우고(in-place) 그다음에 $v_k(s^{i+1})$을 덮어씌운다. 모든 $i$에 대하여 다 덮어씌우고 나서는 다음 $k+1$번째 가치함수에 대하여 똑같이 진행하면 될 것이다.
two-array 방식은 식 (4.5)와 다름없고 따라서 위에서 증명한 것은 two-array 방법에 대한 증명인 셈이다. Sutton 책에 제시된 pseudocode는 in-place 방식이다.

(4.5)에 다시 나오지만 two-array 방식의 PE를 syncronous PE, in-place 방식의 PE를 asyncronous PE라고 부른다.
이렇듯 PE 하나에도 많은 버전이 있다. 나는 V함수에 대한 PE를 증명한 셈이지만, 그것보다는 Q함수에 대한 PE가 더 중요할 수 있다. Q함수에 대해서도 마찬가지로 비슷한 버전의 policy evaluation이 가능하고 심지어 뒤에 나올 policy iteration도 가능할 것이다.
4.1.7 코드 구현
여기서 소개하는 코드 전문의 링크는 여기에 있다.
다음과 같은 Grid World를 생각하자.
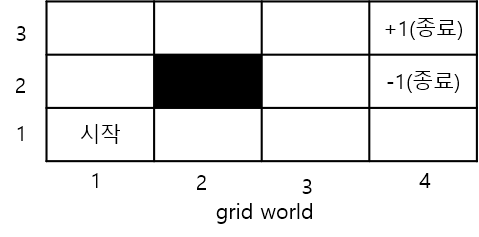
agent는 시작점 $(1,1)$에서 시작하여 $(4,2)$ 또는 $(4,3)$에 도달하면 episode가 끝난다. $(2,2)$와 grid 바깥은 벽이라서 이쪽으로는 이동할 수 없다. 보상은 이동시마다 $-0.1$이 주어지고 두 terminal state $(4,2)$, $(4,3)$에서는 각각 $\pm1$의 보상을 받게 된다.
이 환경에 대하여 equiprobable policy를 생각하자. 그러니까, 상하좌우로 갈 수 있는 확률이 모두 $\frac14$로 일정한 정책을 생각하자. 그리고 이 정책 $\pi$에 대한 가치함수 $v_\pi$를 계산해보자.
사실 가치함수는 벨만방정식을 풀어내어도 답을 얻어낼 수 있다. 벨만방정식은 일차연립방정식이라고 했었으므로 gauss elimination같은걸 사용해도 된다.
위에 썼던 걸 다시 보자. 식 ($\ast$)와 바로 위 식으로부터
\[v_\pi=r_\pi+\gamma Pv_\pi\]이고 따라서 벨만방정식은 다음과 같은 선형연립방정식이 된다.
\[(I-\gamma P)v_\pi=r_\pi\]행렬 $I-\gamma P$와 벡터 $r_\pi$를 가지고 np.linalg.solve 메소드를 사용하면 $v_\pi$함수인 v_array를 얻을 수 있다.
아래는 그 코드이다.
env 모듈은 이 코드에서처럼 정의했다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
from env import GridWorld
import numpy as np
def solve_linear_system(env):
"""
선형 연립방정식을 풀어서 가치함수 구하기
(I - γP)v = r
"""
states = [s for s in env.get_states() if not env.is_terminal(s)]
n_states = len(states)
state_to_idx = {s: i for i, s in enumerate(states)}
# P 행렬과 r 벡터 구성
P = np.zeros((n_states, n_states))
r = np.zeros(n_states)
for i, state in enumerate(states):
# Equiprobable policy: π(a|s) = 0.25
for action in env.actions:
next_state = env.get_next_state(state, action)
reward = env.get_reward(state, action)
prob = 0.25 # equiprobable
# r 벡터: 즉시 보상의 기댓값
r[i] += prob * reward
# P 행렬: 전이 확률
if not env.is_terminal(next_state):
j = state_to_idx[next_state]
P[i, j] += prob
# 선형 시스템 풀기: (I - γP)v = r
I = np.eye(n_states)
A = I - env.gamma * P
v_array = np.linalg.solve(A, r)
# Dictionary로 변환
V = {}
for i, state in enumerate(states):
V[state] = v_array[i]
# Terminal states
for terminal in env.terminals:
V[terminal] = 0.0
return V
# 실행
env = GridWorld()
V_linear = solve_linear_system(env)
print("\n=== Linear System Method (Grid View) ===\n")
for r in range(env.rows - 1, -1, -1):
row_str = ""
for c in range(env.cols):
state = (r, c)
if state == env.wall:
row_str += " [WALL] "
elif state in env.terminals:
row_str += " 0.000 "
else:
row_str += f"{V_linear[state]:7.3f} "
print(row_str)
그러면 그 결과가 아래와 같다.
1
2
3
4
5
=== Linear System Method (Grid View) ===
-0.761 -0.551 -0.142 0.000
-0.865 [WALL] -0.715 0.000
-0.909 -0.913 -0.877 -0.950
terminal state에서의 V값이 0인 것을 확인할 수 있다. $(4,1)$에서의 V값이 무척 작아 -1에 가까운데 그것 또한 당연하다. 이 가치함수에 의하면 시작점에서부터 출발하여 점점 value가 높아지는 쪽으로, 그러니까 위로 두 칸 갔다가 오른쪽으로 세 칸 가는 방식의 경로를 택할 것임을 추측해볼 수 있다.
하지만, 이 포스트의 주제는 벨만방정식이 아니었지. policy evaluation을 통해서도 똑같은 결과가 나오는지 확인하자. 다음에 사용된 코드는 위에 언급한 pseudocode와 정확히 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
def policy_evaluation(env, theta=0.0001, max_iterations=1000):
"""
Equiprobable policy (π(a|s) = 0.25)에 대한 Policy Evaluation
"""
# Value function 초기화
V = {}
for state in env.get_states():
V[state] = 0.0
# Iterative Policy Evaluation
for iteration in range(max_iterations):
delta = 0
# 모든 상태에 대해 업데이트
for state in env.get_states():
if env.is_terminal(state):
continue # 터미널 상태는 V=0 유지
v = V[state]
# Bellman equation for equiprobable policy
new_v = 0
for action in env.actions:
next_state = env.get_next_state(state, action)
reward = env.get_reward(state, action)
# π(a|s) = 0.25 (equiprobable)
prob = 0.25
new_v += prob * (reward + env.gamma * V[next_state])
V[state] = new_v
delta = max(delta, abs(v - new_v))
# 수렴 체크
if delta < theta:
print(f"수렴 완료! (iteration: {iteration + 1})")
break
return V
env = GridWorld()
V = policy_evaluation(env)
# Grid 형태로 시각화
print("\n=== Value Function (Grid View) ===\n")
for r in range(env.rows - 1, -1, -1): # 2, 1, 0 순서 (상하반전)
row_str = ""
for c in range(env.cols):
state = (r, c)
if state == env.wall:
row_str += " [WALL] "
elif state in env.terminals:
row_str += " 0.000 "
else:
row_str += f"{V[state]:7.3f} "
print(row_str)
그 결과는 이전 결과와 같다.
1
2
3
4
5
6
7
수렴 완료! (iteration: 41)
=== Value Function (Grid View) ===
-0.761 -0.551 -0.142 0.000
-0.865 [WALL] -0.715 0.000
-0.909 -0.912 -0.877 -0.950
댓글남기기