Principal Component Analysis
강화학습 글들을 마쳤으니 이제 PCA로 넘어가려 한다. 이 주제에 대해 공부하려고 했었던 이유는, 회사에서 PLS 모델을 자주 쓰는데 이 모델에 대해 내가 잘 알고 있지 못하기 때문이다. PLS와 많이 연관이 있는 것이 PCA라고 들었고 PCA에 대해 모르는 것은 아니지만 그래도 정확하게 알고 넘어가고 싶다는 생각이 들었다.
워낙 데이터과학에서 자주 쓰이는 알고리즘이고 선형대수에서 바로 이어질 수 있는 기법이기 때문에 설명된 자료들이 많다.
- A Tutorial on Principal Component Analysis
- Pattern Recognition and Machine Learning (12.1절)
- Principal Component Analysis(2ed, Jolliffe)
- Principal component analysis with linear algebra
1. motivation
2차원 평면 위의 $n$개의 점들 $X^{(1)}$, $\cdots$ $X^{(n)}$을 생각하자.

이 $n$개의 점들을 가장 잘 설명할 수 있는 직선 $l$을 그어보자. ‘잘 설명할 수 있다’는 것의 의미는
(a) 각 점에서 직선 $l$까지의 거리의 제곱의 평균이 최소가 된다
는 것을 의미한다. (a)는 다음 그림에서 빨간 선들의 길이의 제곱의 평균이 최소가 되는 경우를 뜻한다.
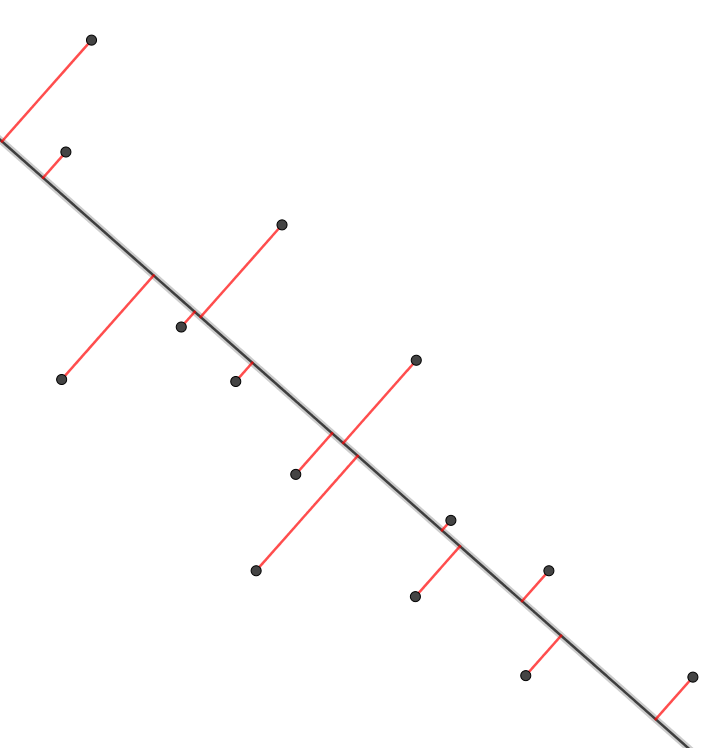
일반성을 잃지 않고 $n$개의 점들의 무게중심이 원점이라고 하자. 원점을 지나는 직선은 방향벡터로 결정되므로, (a)는 빨간 선들의 길이의 제곱의 평균이 최소가 되는 방향벡터 $v$를 구하는 문제가 된다.
조건 (b)를
(b) 직선 $l$ 방향의 분산이 최대가 된다
는 것이라고 하자. 다시 말해, 각 점들의 직선 $l$로의 수선의 발들의 원점까지의 거리의 제곱의 평균이 최대가 되는 경우를 뜻한다. 그러면 (a)와 (b)는 동치이다.
그 이유를 설명하기 위해 다음 그림과 같이 한 점 $X^{(i)}$를 생각하면

피타고라스정리로부터 빨간 선분의 길이의 제곱과 파란 선분의 길이의 제곱의 합은 $\overline{OX^{(i)}}^2$ 으로 일정하다는 사실을 사용할 수 있다.
즉, 점 $X^{(i)}$에서 $l$로의 수선의 발은 $H^{(i)}=\left(X^{(i)}\cdot v\right)v$라고 할 수 있는데 이때, $\lVert H^{(i)}\rVert=X^{(i)}\cdot v$이고 (a)에서 최소화해야 하는 값 $A$는
\[A=\frac1n\sum_{i=1}^n\lVert X^{(i)}-H^{(i)}\rVert^2\]이고 (b)에서 최대화해야 하는 값 $B$는
\[B=\frac1n\sum_{i=1}^n\lVert H^{(i)}\rVert^2\]이다. 그러면 피타고라스 정리로부터
\[\begin{align*} A+B &=\frac1n\sum_{i=1}^n \left(\lVert X^{(i)}-H^{(i)}\rVert^2+\lVert H^{(i)}\rVert^2\right)\\ &=\frac1n\sum_{i=1}^n \lVert X^{(i)}\rVert^2 \end{align*}\]이고 $A+B$의 값이 $v$에 관계없이 일정하다. 따라서 $A$를 최소화하는 것과 $B$를 최대화하는 것은 서로 같은 말이 된다. $v$를 바꿔가면서 $A$(MSE)와 $B$(variance)를 표시해보면, 정말로 MSE가 최소가 될 때 variance가 최대가 됨을 알 수 있다.
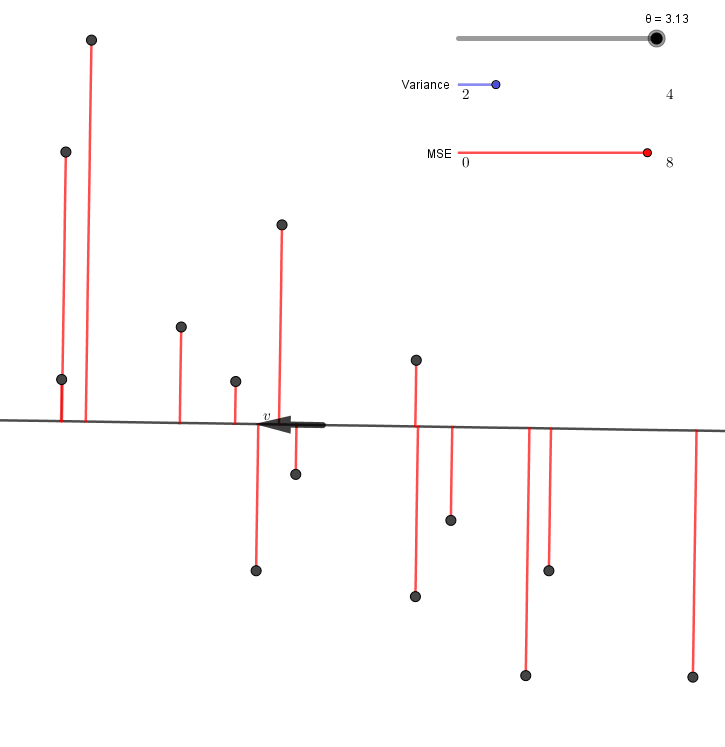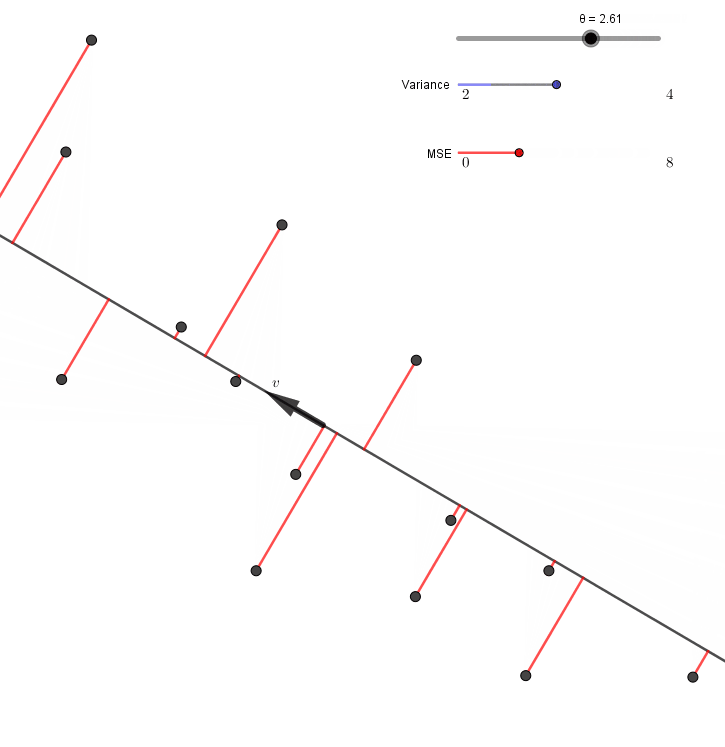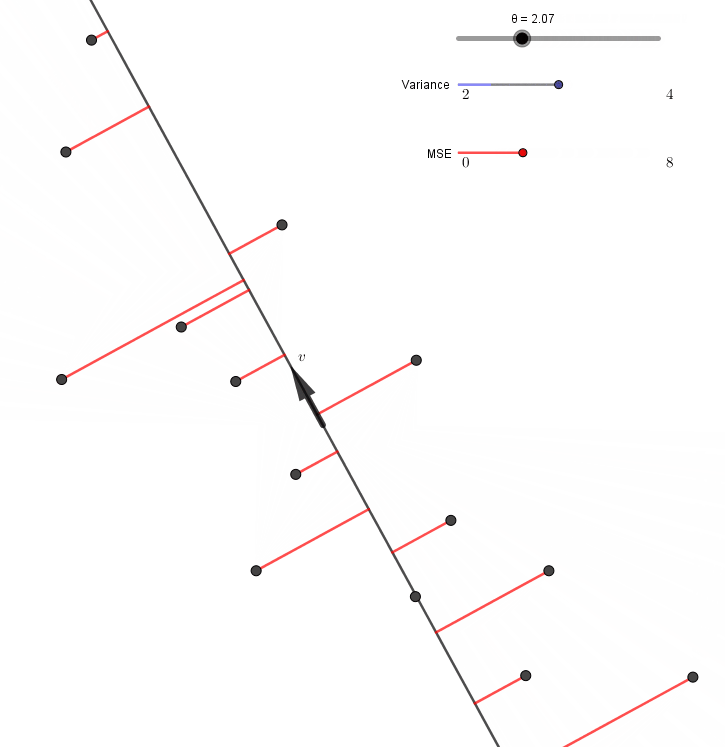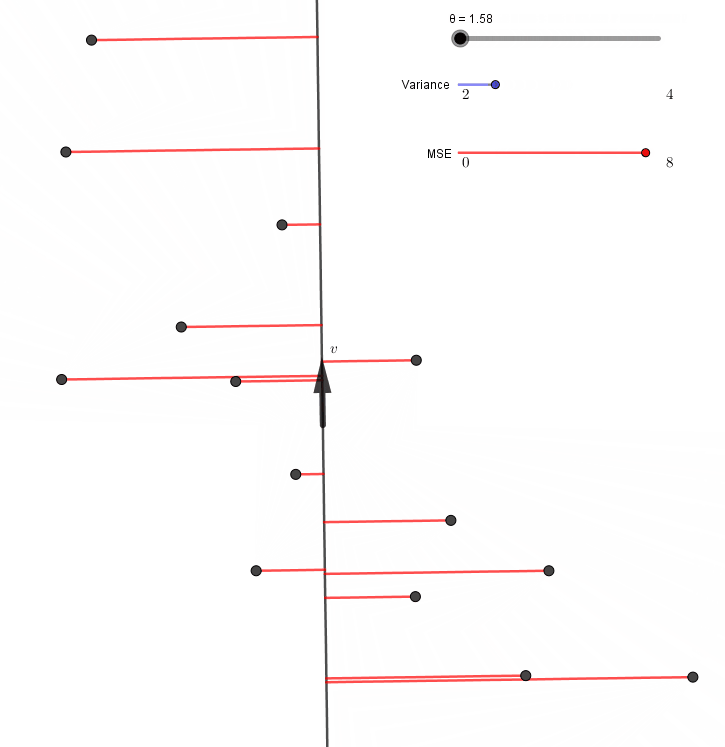
이와 같이 (a) 또는 (b) 조건을 만족시키는 방향 $v$를 주성분이라고 부른다.
이것은 $n$개의 2차원 데이터에서 주성분 1개를 찾는 과정에 해당한다. Pattern Recognition and Machine Learning의 12.1.1, 12.1.2에서는 $N$개의 $D$차원 데이터에서 주성분 $M$개를 찾는 과정에서 Variance를 최대화하는 것이 MSE를 최소화하는 것과 동등함을 설명하고 있다.
2. Preliminaries
2.1 dataset, variance, covariance
다음과 같은 데이터셋이 있다고 하자. 세 학생의 물리 성적과 생물 성적을 나열한 표이다.
| students | physics | biology |
|---|---|---|
| A | 92 | 80 |
| B | 60 | 30 |
| C | 100 | 70 |
각 열은 feature를, 각 행은 datapoint를 의미한다. 이 데이터셋이 나타내는 $3\times 2$ 행렬을 $X$라고 하자;
\[X= \begin{bmatrix} 92&80\\ 60&30\\ 100&70 \end{bmatrix}\]이 행렬의 $i$번째 행벡터를 $X^{(i)}$로, $j$번째 열벡터를 $X_j$로 표기하자. 또한, $j$번째 feature의 평균을 $\mu_j$라고 하자 ($\mu_1=84$, $\mu_2=60$). 그러면 $X_1$, $X_2$의 분산(variance)은 각각
\[\begin{align*} \text{var}(X_1)&=\frac13\left[(92-84)^2+(60-84)^2+(100-84)^2\right]=\frac{896}3\\ \text{var}(X_2)&=\frac13\left[(80-60)^2+(30-60)^2+(70-60)^2\right]=\frac{1400}3 \end{align*}\]으로 계산된다. (여기에서 표본평균과 표본분산이 아닌 모평균과 모분산을 사용하였다.) $X_1$, $X_2$ 사이의 공분산(covariance)은
\[\begin{align*} \text{cov}(X_1,X_2) &=\frac13\left[(92-84)(80-60)+(60-84)(30-60)+(100-84)(70-60)\right]\\ &=\frac{1040}3 \end{align*}\]이다.
일반적으로 $m$개의 feature와 $n$개의 datapoint가 있다고 하면 그 데이터셋은 $n\times m$ 행렬이다. 각 feature들의 평균이 0이라고 하자. 행벡터 $X^{(i)}$는
\[X^{(i)}= \begin{bmatrix} x_{i1}& \cdots& x_{im} \end{bmatrix}\]이고, 열벡터 $X_j$는
\[X_j= \begin{bmatrix} x_{1j}\\ \vdots\\ x_{nj} \end{bmatrix}\]이다. 그러면, $j$번째 feature에 대한 분산은
\[\begin{align*} \text{var}(X_j) &=\frac1n\left({x_{1j}}^2+\cdots+{x_{nj}}^2\right)\\ &=\frac1n\sum_{k=1}^n{x_{kj}}^2\\ &=\frac1n{X_j}^TX_j \tag1 \end{align*}\]이고 $i$번째와 $j$번째 feature 사이의 공분산은
\[\begin{align*} \text{cov}(X_i,X_j) &=\frac1n\left(x_{1i}x_{1j}+\cdots+x_{ni}x_{nj}\right)\\ &=\frac1n\sum_{k=1}^nx_{ki}x_{kj}\\ &=\frac1n{X_i}^TX_j \tag2 \end{align*}\]이다.
2.2 covariance matrix
이번에는 공분산 행렬을 정의해보려 한다. 이 행렬은 $m\times m$ 행렬로서, $i=j$인 경우에는 그 성분이 $X_i$의 분산이고 $i\ne j$인 경우에는 그 성분이 $X_i$와 $X_j$의 공분산인 행렬을 말한다. 그러면 공분산행렬 $C$는 (1)과 (2)로부터
\[C = \frac1n X^TX\tag3\]으로 정의된다. 혹은 다음과 같이 행벡터로서 정의될 수도 있다.
\[\begin{align*} C &=\frac1n\sum_{k=1}^n \begin{bmatrix}x_{k1}\\\vdots\\x_{km}\end{bmatrix} \begin{bmatrix}x_{k1}&\cdots&x_{km}\end{bmatrix}\\ &=\frac1n\sum_{k=1}^n {X^{(k)}}^TX^{(k)} \end{align*}\]당연히, 행렬 $C$는 대칭행렬(symmetric matrix)이다.
2.3 some matrix calculations
$m$차원 벡터 $v=\begin{bmatrix}v_1&\cdots&v_m\end{bmatrix}^T$에 대하여 $v$의 norm은
\[\lVert v\rVert =\sqrt{v^Tv}=\sqrt{v_1^2+\cdots+v_m^2}\]이다. $v^Tv$를 $v$에 대해 미분하면, 즉 gradient를 구하면
\[\frac{\partial}{\partial v}v^Tv =\begin{bmatrix} 2v_1\\\vdots\\2v_m \end{bmatrix} =2v \tag4\]이다. $m\times m$ 행렬 $A$에 대하여 $A$와 $v$의 이차형식(quadratic form)은 $v^TAv$으로 정의된다. 이것을 계산하면
\[\begin{align*} v^TAv &= \begin{bmatrix}v_1&\cdots&v_m\end{bmatrix} \begin{bmatrix} a_{11}&\cdots&a_{1m}\\ \vdots&\ddots&\vdots\\ a_{m1}&\cdots&a_{mm} \end{bmatrix} \begin{bmatrix}v_1\\\vdots\\v_m\end{bmatrix}\\ &= \begin{bmatrix} \sum_{i=1}^ma_{i1}v_i&\cdots\sum_{i=1}^ma_{im}v_i \end{bmatrix} \begin{bmatrix}v_1\\\vdots\\v_m\end{bmatrix}\\ &=\sum_{i=1}^m\sum_{j=1}^ma_{ij}v_iv_j \end{align*}\]이것을 $v$의 한 성분 $v_k$에 대하여 편미분하면
\[\begin{align*} \frac\partial{\partial v_k}a_{kk}v_kv_k&=2a_{kk}v_k\\ \frac\partial{\partial v_k}a_{ik}v_iv_k&=a_{ik}v_i (i\ne k)\\ \frac\partial{\partial v_k}a_{kj}v_kv_j&=a_{kj}v_j (j\ne k) \end{align*}\]로부터
\[\frac\partial{\partial v_k}v^TAv=\sum_{i=1}^ma_{ik}v_i+\sum_{j=1}^ma_{kj}v_j\]이다. 만약 $A$가 대칭행렬이면
\[\frac\partial{\partial v_k}v^TAv=2\sum_{j=1}^ma_{kj}v_j\]이다. $v^TAv$를 $v$에 대해 미분하면, 즉 gradient를 구하면,
\[\begin{align*} \frac\partial{\partial v}v^TAv &=2\begin{bmatrix} \sum_{j=1}^ma_{1j}v_j\\ \vdots\\ \sum_{j=1}^ma_{mh}v_j \end{bmatrix}\\ &=2\begin{bmatrix} a_{11}&\cdots&a_{1m}\\ \vdots&\ddots&\vdots\\ a_{m1}&\cdots&a_{mm}\\ \end{bmatrix} \begin{bmatrix} v_1\\\vdots\\v_m \end{bmatrix}\\ &=2Av \tag5 \end{align*}\]2.4 real symmetric matrices
만약 $A$가 real symmetric이면 (실수로 이루어진 대칭행렬이면) 다음이 성립한다.
- (a) $A$의 모든 eigenvalue는 실수이다
- (b) $A=BDB^{-1}$를 만족시키는 대각행렬 $D$와 직교행렬 $B$가 존재한다. (직교대각화 가능)
이에 관한 설명은 행렬의 직교대각화 포스팅에서 정리 19와 성질 20으로 갈음한다.
따라서 (3)에서 정의된 $C$는 실수인 eigenvalue만을 가진다. 특히, $C$는 nonnegative한 eigenvalue만을 가진다 (positive semidefinite). 왜냐하면, 만약 $Cv=\lambda v$이면
\[\begin{align*} \frac1nX^TXv&=\lambda v\\ \frac1n(Xv)^T(Xv)=\lambda v^Tv\\ \frac1n\lVert Xv\rVert^2=\lambda\lVert v\rVert^2 \end{align*}\]이기 때문이다.
2.5 Lagrange multiplier method
두 함수 $f:\mathbb R^n\to\mathbb R$와 $g:\mathbb R^n\to\mathbb R^m$에 대하여 ($f,g\in C^1$) 최적화 문제
는 함수 $\mathcal L:\mathbb R^n\times\mathbb R^m\to\mathbb R$을
\[\mathcal L\left(\boldsymbol x,\boldsymbol\lambda\right)=f(\boldsymbol x)+\boldsymbol\lambda^Tg(\boldsymbol x)\]로 정의하여 ($\boldsymbol\lambda\in\mathbb R^m$)
를 풀어도 된다. 이에 관해서는 직전 포스트에 자세히 설명해놓았다.
3. Principal Component Analysis
2.1에서와 같이 $m$개의 feature와 $n$개의 datapoint가 있다고 하자. 즉, $n\times m$ 행렬로 표현되는 데이터셋을 생각하고 각 feature들의 평균이 0이라고 하자.
3.1 definition of PCs
$m$개의 feature들 $X_j$을 일차결합하여 새로운 성분을 만들되, 의미있는 성분을 만들어보려 한다. $X_j$들을 일차결합이란, 벡터 $v_1\in\mathbb R^m$에 대하여 ($\lvert v_1\rvert=1$) $Xv_1$을 뜻한다. 왜냐하면
\[Xv_1 = \begin{bmatrix} X_1&\cdots&X_m \end{bmatrix} \begin{bmatrix} v_{11}\\\vdots\\v_{1m} \end{bmatrix} =\sum_{j=1}^mv_{1j}X_j\]이기 때문이다. 또한, ‘의미있는 성분’이라 함은 주어진 데이터셋을 가장 잘 설명하는 성분을 말하며, 의미있는 성분을 찾는다는 것은 다음 둘 중 하나의 조건을 만족시키는 방향 $v_1$를 찾는 것이다.
(a) $v_1$ 방향으로의 분산이 최대가 된다.
(b) $v_1$ 방향의 직선까지의 거리가 최소가 된다.
1에서 증명한 것과 비슷한 논리를 적용하면 (a)와 (b)가 동등한 조건임을 확인할 수 있고 따라서 (a)조건만을 고려하자.
가장 중요한 첫번째 주성분을 구했으니 여기서 끝내도 되겠지만, $K\le m$인 $K$에 대하여 $K$개의 주성분을 구할 수 있다. 예를 들어 두번째 주성분 $Xv_2$의 정의는 다음과 같다.
$k$번째 주성분이 구해졌을 때, $k+1$번째 주성분은 다음과 같이 정한다.
3.2 derivation of PCs
첫번째 주성분을 구해보자. 2.1에서 분산을 구하는 식 (1)과 공분산행렬의 정의 (3)에 의해
\[\begin{align*} \text{var}(Xv_1) &=\frac1n(Xv_1)^TXv_1\\ &=\frac1n{v_1}^TX^TXv_1\\ &={v_1}^T\left(\frac1nX^TX\right)v_1\\ &={v_1}^TCv_1 \end{align*}\]따라서 $v_1$은 ${v_1}^Tv_1=1$를 만족시키면서 ${v_1}^TCv_1$을 최대화하는 벡터이다. 이 최적화 문제에 대한 lagrangian은
\[\mathcal L_1(v_1,\lambda)={v_1}^TCv_1+\lambda(1-{v_1}^Tv_1)\]이다. 양변을 $v_1$으로 미분하면 (4), (5)에 의해
\[0=2Cv_1-2\lambda v_1\]이다. 따라서 $(C-\lambda I)v_1=0$이고 $\lambda$은 $C$에 대한 eigenvalue이고 $v_1$은 그 eigenvalue에 대한 eigenvector이다. 이때 최대화되어야 하는 값은
\[\text{var}(Xv_1)={v_1}^TCv_1={v_1}^T(\lambda_1v_1)=\lambda_1 {v_1}^Tv_1=\lambda\]이고 $C$의 eigenvalue들은 모두 nonnegative이므로, $\lambda$은 $C$의 eigenvalue 중에서 가장 큰 값 $\lambda_1$이 된다. 만약 $\lambda_1=0$이면 $C$는 영행렬이고 $X$도 $X=0$이므로 $\lambda_1\ne0$이라고 가정하자. 즉 trivial한 경우를 제외하면 $\lambda_1\gt0$이라고 둘 수 있다.
다음으로 두번째 주성분을 구해보자. 먼저
\[\text{var}(Xv_2)={v_2}^TCv_2\]이다. 따라서 $v_2$은 ${v_2}^Tv_2=1$와 $(Xv_2)^TXv_1=0$를 만족시키면서 ${v_2}^TCv_2$을 최대화하는 벡터이다. 이때
\[\begin{aligned} (Xv_2)^TXv_1&=0\\ {v_2}^TX^TXv_1&=0\\ {v_2}^TCv_1&=0\\ {v_2}^T(\lambda_1 v_1)&=0\\ \lambda_1{v_2}^Tv_1&=0\\ {v_2}^Tv_1&=0 \end{aligned} \tag6\]이다. 즉, (6)의 모든 식들은 동치이다. 따라서 이 최적화 문제에 대한 lagrangian은
\[\mathcal L_2(v_2,\lambda,\phi)={v_2}^TCv_2+\lambda(1-{v_2}^Tv_2)+\phi{v_2}^Tv_1\]이다.
양변을 $v_2$에 대해 미분하면 $\frac{\partial\mathcal L_2}{\partial v_2}=0$으로부터
\[0=2Cv_2-2\lambda v_2+\phi v_1\tag7\]양변의 좌측에 ${v_1}^T$을 곱하면
\[\begin{align*} 0&=2{v_1}^TCv_2-2\lambda{v_1}^Tv_2+\phi\lambda{v_1}^Tv_1\\ 0&=0+0+\phi\cdot1 \end{align*}\]이라서 $\phi=0$이다.
그러면 (7)은
\[0=2Cv_2-2\lambda v_2\]이 되고, 따라서 $0=(C-\lambda I)v_2$이다. 그러면 $\lambda$는 $C$의 eigenvalue이고 $v_2$는 그 $\lambda$에 대한 eigenvector이다. 최대화되어야 하는 값은 $\text{var}(Xv_2)=\lambda$이다.
만약 $\lambda_1$의 algebraic multiplicity가 1이었다면, $\lambda=\lambda_1$이 될 수 없다. $v_2\parallel v_1$이 되어 사실상 같은 방향이 되어버리기 때문이다. 따라서 $\lambda$는 $C$의 eigenvalue들 중 두번째로 큰 값인 $\lambda_2$가 된다. 만약 $\lambda_1$의 algebraic multiplicity가 2보다 컸다면, $\lambda=\lambda_1$이다. $v_2$가 $v_1$과 다른 방향이 될 수 있기 때문이다.
즉, $C$의 characteristic equation의 근을 $\lambda_1\ge\lambda_2\ge\cdots$라고 하고, $\lambda_1$에 대한 eigenvector를 $v_1$, $\lambda_2$에 대한 eigenvector를 $v_2$라고 할 때, $Xv_1$가 첫번째 주성분, $Xv_2$가 두번째 주성분인 것이다.
이번에는 일반적으로, 다음과 같은 가정하에서 $k$번째 주성분을 구해보자.
- 첫번째, 두번째, $\cdots$, $k-1$번째 주성분은 각각 $Xv_1$, $Xv_2$,$\cdots$, $Xv_{k-1}$이고, $v_1$, $v_2$,$\cdots$, $v_{k-1}$는 eigenvalue $\lambda_1$, $\lambda_2$,$\cdots$, $\lambda_{k-1}$에 대한 eigenvector이다. 이때, $\lambda_i$들은 $\lambda_1\ge\lambda_2\ge\cdots\ge\lambda_{k-1}\gt0$를 만족시키는 $C$의 characteristic equation의 가장 큰 $k-1$개의 eigenvalue들이다.
- $1\le i\lt j\le k-1$인 $i$, $j$에 대하여 ${v_i}^Tv_j=0$이다.
${v_k}^TCv_k$는
\[\text{var}(Xv_k)={v_k}^TCv_k\]이므로, $v_k$는 ${v_k}^Tv_k=1$와 $(Xv_k)^TXv_k=0$을 만족시키면서 ($1\le i\le k-1$) ${v_k}^TCv_k$를 최대화하는 벡터이다. (6)에서처럼
\[\begin{align*} {v_k}^TCv_i&=0\\ {v_k}^Tv_i&=0 \end{align*}\]이다. 그러면 이 최적화문제에 대한 lagrangian은
\[\mathcal L_k(v_k,\lambda,\phi_1,\cdots,\phi_{k-1})={v_k}^TCv_k+\lambda(1-{v_k}^Tv_k)+\phi_1{v_k}^Tv_1+\cdots+\phi_{k-1}{v_k}^Tv_{k-1}\]이다. 양변을 $v_k$에 대해 미분하면 $\frac{\partial\mathcal L_k}{\partial v_k}=0$으로부터
\[0=2Cv_k-2\lambda v_k+\phi_1v_1+\cdots+\phi_{k-1}v_{k-1}\tag8\]$1\le i\le k-1$인 $i$에 대하여 양변에 ${v_i}^T$를 왼쪽에 곱하면
\[\begin{align*} 0&=2{v_i}^TCv_k-2\lambda{v_i}^Tv_k+\phi_1{v_i}^Tv_1+\cdots+\phi_{k-1}{v_i}^Tv_{k-1}\\ 0&=0-0+0+\cdots\phi_i\cdot1+\cdots+0\\ \end{align*}\]이므로 $\phi_i=0$이다. 그러면 (8)은
\[0=2Cv_k-2\lambda v_k\]이 되고, $0=(C-\lambda I)v_k$가 되어 $\lambda$는 $C$의 eigenvalue이고 $v_k$는 그 $\lambda$에 대한 eigenvector이며 최대화되어야 하는 값은 $\text{var}(Xv_k)=\lambda$이다.
따라서, $C$의 characteristic equation의 근을 $\lambda_1\ge\lambda_2\ge\cdots\ge\lambda_k\ge\cdots$라고 하고, $\lambda_1$에 대한 eigenvector를 $v_1$, $\lambda_2$에 대한 eigenvector를 $v_2$, $\lambda_k$에 대한 eigenvector를 $v_k$라고 할 때, $Xv_1$가 첫번째 주성분, $Xv_2$가 두번째 주성분, $Xv_k$가 $k$번째 주성분인 것이다. 이렇게 하면 $n$번째 주성분 $Xv_m$까지 구할 수 있다. 도중에 $\lambda_k=0$인 경우가 나온다면, $\lambda_{k+1}=\cdots=\lambda_n=0$이 될 것이며 그에 해당하는 eigenvector들 $v_{k+1}$, $\cdots$, $v_n$도 구해질 수 있다.
3.3 PCA and orthogonal diagonalization
이상을 요약하여 orthogonal diagonalization과 함께 적어보면 다음과 같다.
데이터셋 $X$에 대하여 공분산행렬 $C$가 $C=\frac1nX^TX$라고 할 때, $C$는 real symmetric 행렬이므로 eigenvalue들이 모두 실수이고 eigenvector들이 서로 직교한다. 더 나아가, $C$는 positive semidefinite이므로 eigenvalue들은 모두 nonnegative이다.
orthogonal diagonalization에 의해 eigenvalue들과 eigenvector들을 얻어낼 수 있다. 이때,
이때, eigenspace의 차원이 2차원 이상일 수 있으므로 $v_i$는 (따라서 $i$번째 주성분은) 반드시 유일하지 않을 수 있다.
댓글남기기